Навигация
Если в матрице есть нулевая строка, то все строки ниже нее также нулевые;
1. если в матрице есть нулевая строка, то все строки ниже нее также нулевые;
2. пусть aij не равное 0 -- первый ненулевой элемент в строке с индексом i, т.е. элементы ail = 0 при l < j. Тогда все элементы в j-м столбце ниже элемента aij равны нулю, и все элементы левее и ниже aij также равны нулю: akl = 0 при k > i и l =< j.
Ступенчатая матрица выглядит так:
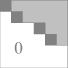
Здесь тёмными квадратиками отмечены первые ненулевые элементы строк матрицы. Белым цветом изображаются нулевые элементы, серым цветом - произвольные элементы.
Алгоритм Гаусса использует элементарные преобразования матрицы двух типов.
· Преобразование первого рода: две строки матрицы меняются местами, и при этом знаки всех элементов одной из строк изменяются на противоположные.
· Преобразование второго рода: к одной строке матрицы прибавляется другая строка, умноженная на произвольное число.
Элементарные преобразования сохраняют определитель и ранг матрицы, а также множество решений линейной системы. Алгоритм Гаусса приводит произвольную матрицу элементарными преобразованиями к ступенчатому виду. Для ступенчатой квадратной матрицы определитель равен произведению диагональных элементов, а ранг - числу ненулевых строк (рангом по определению называется размерность линейной оболочки строк матрицы).
Метод Гаусса в математическом варианте состоит в следующем:
1. ищем сначала ненулевой элемент в первом столбце. Если все элементы первого столбца нулевые, то переходим ко второму столбцу, и так далее. Если нашли ненулевой элемент в k-й строке, то при помощи элементарного преобразования первого рода меняем местами первую и k-ю строки, добиваясь того, чтобы первый элемент первой строки был отличен от нуля;
2. используя элементарные преобразования второго рода, обнуляем все элементы первого столбца, начиная со второго элемента. Для этого от строки с номером k вычитаем первую строку, умноженную на коэффициент ak1/a11 .
3. переходим ко второму столбцу (или j-му, если все элементы первого столбца были нулевыми), и в дальнейшем рассматриваем только часть матрицы, начиная со второй строки и ниже. Снова повторяем пункты 1) и 2) до тех пор, пока не приведем матрицу к ступенчатому виду.
Программистский вариант метода Гаусса имеет три отличия от математического:
1. индексы строк и столбцов матрицы начинаются с нуля, а не с единицы;
2. недостаточно найти просто ненулевой элемент в столбце. В программировании все действия с вещественными числами производятся приближенно, поэтому можно считать, что точного равенства вещественных чисел вообще не бывает. Некоторые компиляторы даже выдают предупреждения на каждую операцию проверки равенства вещественных чисел. Поэтому вместо проверки на равенство нулю числа aij следует сравнивать его абсолютную величину ij с очень маленьким числом ε (например, ε = 0.00000001). Если ij=< ε, то следует считать элемент aij нулевым;
3. при обнулении элементов j-го столбца, начиная со строки i + 1, мы к k-й строке, где k > i, прибавляем i-ю строку, умноженную на коэффициент r = -akj/aij :
Такая схема работает нормально только тогда, когда коэффициент r по абсолютной величине не превосходит единицы. В противном случае, ошибки округления умножаются на большой коэффициент и, таким образом, экспоненциально растут. Математики называют это явление неустойчивостью вычислительной схемы. Если вычислительная схема неустойчива, то полученные с ее помощью результаты не имеют никакого отношения к исходной задаче. В нашем случае схема устойчива, когда коэффициент r = -akj/aij не превосходит по модулю единицы. Для этого должно выполняться неравенство Отсюда следует, что при поиске разрешающего элемента в j-м столбце необходимо найти не первый попавшийся ненулевой элемент, а максимальный по абсолютной величине. Если он по модулю не превосходит ε, то считаем, что все элементы столбца нулевые; иначе меняем местами строки, ставя его на вершину столбца, и затем обнуляем столбец элементарными преобразованиями второго рода.
Основная идея метода Гаусса- привести матрицу систему к диагональному виду, то есть все элементы главной диагонали –нули. Для приведения матрицы к такому виду, мы выбираем самую верхнюю строку матрицы, и вычитаем её из всех остальных строк, умножив её для каждой строки на некий коэффициент, так, что самый левый столбец ниже главной диагонали заполнен нулями. Вычитаемая с коэффициентом строка называется текущей строкой. Выбирая текущую строку вначале верхнюю, а потом всё ниже и ниже, мы добьёмся, что все элементы ниже главной диагонали будет равны нулю. Эту часть метода- обработка строк по текущей строке и предстоит распараллеливать.
Суть метода заключается в последовательном исключении неизвестных. Рассмотрим систему линейных уравнений:
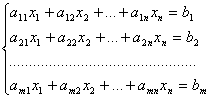
Разделим обе части 1–го уравнения на a11 0, затем: 1) умножим на а21 и вычтем из второго уравнения 2) умножим на а31 и вычтем из третьего уравнения и т.д. Получим:, где d1j = a1j/a11, j = 2, 3, …, n+1. dij= aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1. Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
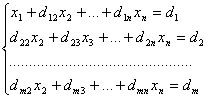
Пример. Решить систему линейных уравнений методом Гаусса.
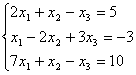
Составим расширенную матрицу системы.
А* =
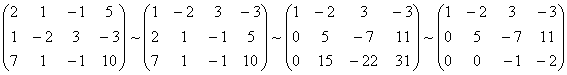
Таким образом, исходная система может быть представлена в виде:
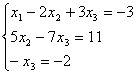 ,
,
откуда получаем:x3 = 2;x2 = 5;x1= 1.
Пример. Решить систему методом Гаусса.
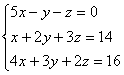
Составим расширенную матрицу системы.
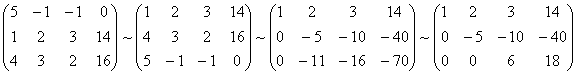
Таким образом, исходная система может быть представлена в виде:
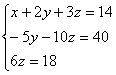 ,
,
откуда получаем: z = 3; y = 2;x =1.
Работа с файлами.Стандартная библиотека С++ содержит набор функций для работы с файлами. Эти функции описаны в стандарте ANSI. Отметим, что файловый ввод-вывод не является частью языка С+, и ANSI-функции - не единственное средство ввода-вывода. Так, в операционной системе Unix более популярен другой набор функций ввода-вывода, который можно использовать не только для работы с файлами, но и для обмена по сети. В C++ часто используются библиотеки классов для ввода-вывода. Тем не менее, функции ANSI-библиотеки поддерживаются всеми С++-компиляторами, и потому программы, применяющие их, легко переносятся с одной платформы на другую. Прототипы функций ввода-вывода и используемые для этого типы данных описаны в стандартном заголовочном файле "stdio.h.
Открытие файла: функция fopen.Для доступа к файлу применяется тип данных FILE. Это структурный тип, имя которого задано с помощью оператора typedef в стандартном заголовочном файле "stdio.h". Программисту не нужно знать, как устроена структура типа файл: ее устройство может быть системно зависимым, поэтому в целях переносимости программ обращаться явно к полям структуры FILE запрещено. Тип данных "указатель на структуру FILE используется в программах как черный ящик: функция открытия файла возвращает этот указатель в случае успеха, и в дальнейшем все файловые функции применяют его для доступа к файлу.
Здесь path - путь к файлу (например, имя файла или абсолютный путь к файлу), mode - режим открытия файла. Строка mode может содержать несколько букв. Буква "r" (от слова read) означает, что файл открывается для чтения (файл должен существовать). Буква "w" (от слова write) означает запись в файл, при этом старое содержимое файла теряется, а в случае отсутствия файла он создается. Буква "a" (от слова append) означает запись в конец существующего файла или создание нового файла, если файл не существует.
В некоторых операционных системах имеются различия в работе с текстовыми и бинарными файлами (к таким системам относятся MS DOS и MS Windows; в системе Unix различий между текстовыми и бинарными файлами нет). В таких системах при открытии бинарного файла к строке mode следует добавлять букву "b" (от слова binary), а при открытии текстового файла -- букву "t" (от слова text). Кроме того, при открытии можно разрешить выполнять как операции чтения, так и записи; для этого используется символ + (плюс). Порядок букв в строке mode следующий: сначала идет одна из букв "r", "w", "a", затем в произвольном порядке могут идти символы "b", "t", "+". Буквы "b" и "t" можно использовать, даже если в операционной системе нет различий между бинарными и текстовыми файлами, в этом случае они просто игнорируются.
3.Описание алгоритма решения СЛАУ методом Гаусса
Составить программу решения систем линейных алгебраических уравнений с матрицей порядка n методом Гаусса с использованием языка С++ .
Алгоритм решения системы линейных уравнений с помощью метода Гаусса. Алгоритм реализован на языке С++.
Пусть у нас есть система N линейных уравнений
a11x1 + a12x2 + a13x3 + ... a1NxN = b1
a21x1 + a22x2 + a23x3 + ... a2NxN = b2
a31x1 + a32x2 + a33x3 + ... a3NxN = b3
...
aN1x1 + aN2x2 + aN3x3 + ... aNNxN = bN
где xi - неизвестные, aij - коэффициенты при неизвестных, bi - свободные члены в уравнениях, i,j пробегают значения от 1 до N.
Цель задачи - зная aij и bi найти xi.
Суть метода Гаусса состоит в том, что с помощью некоторых операций исходную систему уравнений можно свести к более простой системе. Эта простая система имеет треугольный вид:
| a11x1 + | a12x2 + | a13x3 + | ... | a1NxN = b1 |
| a22x2 + | a23x3 + | ... | a2NxN = b2 | |
| a33x3 + | ... | a3NxN = b3 | ||
| ... | ||||
| ... | aNNxN = bN |
Особенность этой системы - в строках с номером i все коэффициенты aij при j<i равны нулю.
Если мы смогли привести нашу систему уравнений к такому треугольному виду, то решить уравнения уже просто. Из последнего уравнения находим xN= bN / aNN. Дальше подставляем его в предпоследнее уравнение и находим из него xN-1. Подставляем оба найденных решения в следующее с конца уравнение и находим xN-2. И так далее, пока не найдем x1, на чем решение заканчивается. Такая процедура называется обратной прогонкой.
Теперь перейдем к вопросу как же добиться того, чтобы система стала треугольной.
Из линейной алгебры известно что если к некоторой строке системы уравнений прибавить любую линейную комбинацию любых других строк этой системы, то решение системы не изменится. Под линейной комбинацией строк понимается сумма строк, каждая из которых умножается на некоторое число (в принципе, любое).
Нужно, чтобы во второй строке получилось уравнение, в которой отсутствует член при x1. Прибавим к этой строке первую строку, умноженную на некоторое число M.
(a11x1 + a12x2 + a13x3 + ... a1NxN = b1)*M +
a21x1 + a22x2 + a23x3 + ... a2NxN = b2
Получим
(a11*М + a21) x1 + ... = b1*M + b2
Для того, чтобы член при x1 равнялся нулю, нужно, чтобы M = - a21 / a11. Проделав эту операцию, получившееся уравнение запишем вместо второго и приступим к третьему уравнению. К нему мы прибавим первое уравнение, умноженное на M = - a31 / a11 и тоже получим ноль вместо члена при x1. Такую операцию нужно проделать над всеми остальными уравнениями. В результате получим систему такого вида:
| a11x1 + | a12x2 + | a13x3 + | ... | a1NxN = b1 |
| a22x2 + | a23x3 + | ... | a2NxN = b2 | |
| a32x2 + | a33x3 + | ... | a3NxN = b3 | |
| ... | ||||
| aN2x2 + | aN3x3 + | ... | aNNxN = bN |
После этого будем избавляться от членов при x2 в третьем, четвертом, N-ом уравнении. Для этого нужно к уравнению с j-м номером прибавить 2-ое уравнение, умноженное на M = - aj2 / a22. Проделав эту операцию над всеми остальными уравнениями, получим систему где нет членов с x2 в уравнениях с номером больше 2.
И так далее... Проделав это для третьего члена, четвертого... до тех пор, пока не кончатся уравнения, получим в итоге систему треугольного вида.
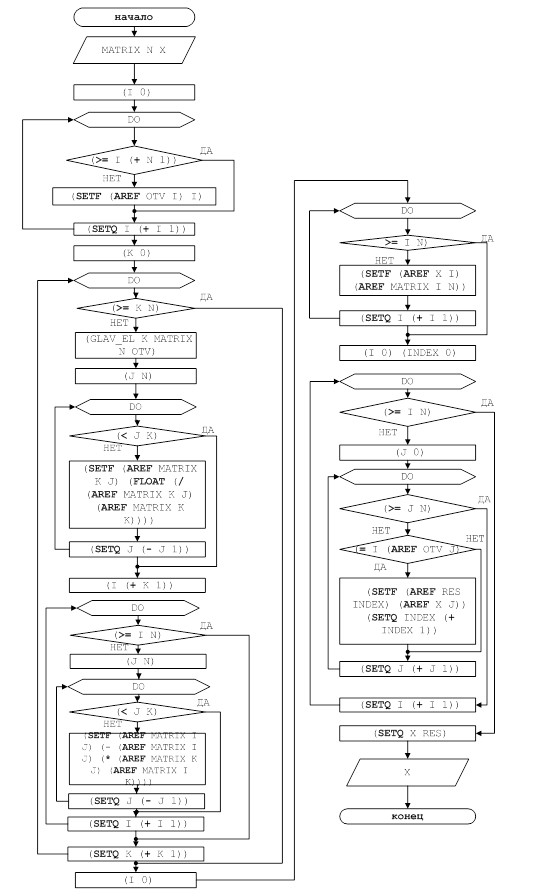
Алгоритм описан в псевдокоде (команды в виде текста на русском языке).
ПРОЦЕСС 0: (главный процесс)
1.Разослать всем процессам количество текущих строк.
(Или не всем процессам, если процессов больше чем строк).
2.ЦИКЛ ПО СТРОКАМ (выбор текущей строки)
1.Разослать всем процессам текущую строку.
(Если число процессов больше чем осталось строк для обработки (строк ниже текущей строки), то разослать текущую строку не всем процессам, а только тем, которые будут задействованы в обработке строк.)
2.Разослать всем процессам строки для обработки (посылаем строку, затем строки в матрице). Разделить между процессами строки ниже текущей. Разделяем так в цикле по строкам раздаём по одной каждому процессу, пока не кончатся строки, по процессам 1..N идём циклически.
3.Разослать всем процессам количества строк, посланных им для обработки.
4.Принять от процессов 1..N обработанные строки, занести их в матрицу. (Принимаем строку и номер строки в матрице)
5.Выбрать следующую текущую строку - новый шаг цикла.
КОНЕЦ ЦИКЛА
3.Вычислить решение системы по диагональной матрице.
4.Выдать результат работы.
5.Завершить работу.
ПРОЦЕСС 1..N:
1.Принимаем количество текущих строк.
2.ЦИКЛ ОБРАБОТКИ ПОЛУЧЕННЫХ СТРОК
1.Принимаем сообщение о количестве строк для обработки
2.Если число строк для обработки >0 то:
{
1.Принимаем сообщение с текущей строкой
2.ЦИКЛ обработки строк
1.Принимаем сообщение со строкой для обработки .
(получаем ещё номер строки в матрице).
2.Обрабатываем полученную строку
3.Посылаем главному процессу результаты работы. Для каждой строки посылаем строку и номер строки.
4.Идём на новый шаг цикла обработки строк.
3.Синхронизируемся .
}
3.Завершить процесс.
4.Исходный текст программы
Составить программу решения систем линейных алгебраических уравнений с квадратной невырожденной матрицей порядка n методом Гаусса с использованием языка С++ .
// Решение системы линейных уравнений методом Гаусса.
#include<io.h>
#include "stdio.h"
#include "conio.h"
#include <windows.h>
#include <iostream>
#include <time.h>
#include <io.h>
#include <fcntl.h>
#include <string.h>
#include "stdafx.h"
using namespace std;
#include <stdio.h> // Описания функций ввода-вывода
#include <math.h> // Описания математических функций
#include <stdlib.h> // Описания функций malloc и free
const int n=3;
void ReadData()
{
int n;
double A[n][n];
FILE*f=fopen("l1.txt","rt");
if (f!=0)
printf("CAN'T OPEN FILE\nPlease, f**k off!");
{
fscanf(f,"%d",&n);
printf("Sborka matritsi m- na n-:\n");
for (int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
fscanf(f,"%d",&A[i][j]);
printf("%d",A[i][j]);
}
printf("\n");
}
printf("\n\n");
fclose(f);
}
}
void Gauss
( double X[n], const double Z[n][n], const double Y[n])
{
ReadData();
double A[n][n]; // матрица коэффицентов Гаусса
double B[n]; // рабочий массив свободных членов
int i,
int j,
int k; // рабочие переменные
for( i = 0; i < n; i++ ) // копирование в рабочую матрицу A
{
for( j = 0; j < n; j++ )
A[i][j] = Z[i][j];
B[i] = Y[i]; // копирование свободных членов
X[i] = 0;
}
for( k = 0; k < n-1; k++ )
for( i = k+1; i < n; i++ ) // преобразование строк
{
double r = A[i][k] / A[k][k];
for( j = k; j < n; j++ )
A[i][j] -= A[k][j] * r;
B[i] -= B[k] * r;
}
X[n-1] = B[n-1] / A[n-1][n-1];
for( i = n-2; i >= 0; i-- )
{
double s = 0;
for( j = i+1; j < n; j++ )
s += A[i][j] * X[j];
X[i] = ( B[i] - s ) / A[i][i];
}
printf( "\n" );
for( i = 0; i < n; i++ )
{ printf( "\n" );
for( j = 0; j < n; j++ )
printf( "%8.2lf", A[i][j] );
printf( " %8.2lf", B[i] );
}
}
/* ------------------------------------------------- */
void main( void )
{
ReadData();
double X[n];// корни системы линейных уравнений
short i, j; // рабочие переменные
printf( " matritsa A* matritsa B\n" );
for( i = 0; i < n; i++ ) // цикл строк
{
printf( "\n" ); // новая строка на мониторе
for( j = 0; j < n; j++ )
printf( "%8.2lf", A[i][j] );
printf( " %8.2lf", B[i] );
}
printf( "\n" );
printf( "stypen4atii vid matritsi \n" );
Gauss( X, A, B ); // решение методом Гаусса
printf( "\n" );
printf( "\n" );
printf( " zna4enia peremennih x1,x1,x3\n" );
printf( "\n X = " );
for( i = 0; i < n; i++ )
printf( "%8.2lf", X[i] );
printf( "\n" );
printf( "\n" );
printf( "rang=\n" );
getch();
}
5.Тестирование программы
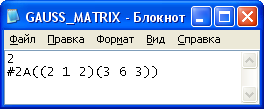
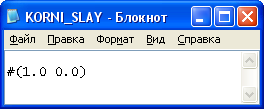
Результаты решения системы с тремя неизвестными:
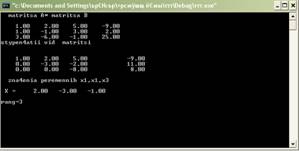
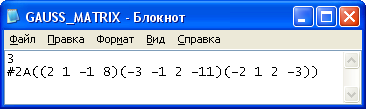
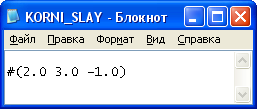
Результаты решения системы с четырьмя неизвестными:
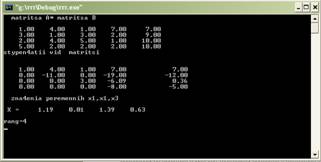
Данные в файле:
Имя файла l1
4
2 1 4 1
3 1 3 2
2 4 5 1
5 2 2 2
Размерности матриц=4
Матрица А
2 1 4
3 1 3
2 4 5
5 2 2
Матрица В
1
2
1
2
Вывод
В результате выполнения курсового проекта были разработаны два класса функций для решения простейших задач линейной алгебры. Число этих функций сравнительно невелико, однако можно легко добавить в эти классы более сложные функции, построенные на базе уже имеющихся. Классы позволяют работать с матрицами и векторами, элементы которых могут быть любого типа, однако на практике чаще всего используется целый тип и тип чисел с плавающей запятой. Классы написаны на языке С++, однако могут быть легко переписаны на любом из современных языков программирования, так как приведены довольно простые алгоритмы всех компонентных функций. Были максимально предусмотрены всевозможные ошибки, которые могут возникнуть при использовании функций данных классов. Особое внимание уделялось разумному выделению памяти подобъекты во время выполнения программы, поэтому все функции были тщательно отлажены.Классы Matrix и Vector могут быть эффективно применены на практике в задачах, требующих операций с матрицами и векторами, а также связанных с решением систем линейных алгебраических уравнений.
Список литературы
1. Начальный курс С и С++.: Учебник. /Б. И. Березин. Москва:"ДИАЛОГ-МИФИ",1999г.
2. Язык программирования С++. : Учебник. /. Страуструп. Киев:"ДиаСофт", 1993 г.
3. Введение в язык С++: Учебник. / Бьярн Страустрап.
– СПб.: 1995.
4. Структуры и алгоритмы обработки данных: Учебник. / Матьяш В.А., Путилов В.А., Фильчаков В.В. , Щёкин С.В. - Апатиты, КФ ПетрГУ, 2000
5. С++ /Дэвис Стефан Р.,4-е издание : Пер. с англ.:- М.: Издательский дом «Вильямс»,2003
6. Основы программирования: Учеб. Для сред. проф. образования /И.Г.Семакин, А.П.Шестаков. – М., 2006.
7. С++ экспресс курс: Учебник. /Лаптев В.В. – СПб.: БХВ- Петербург 2004.
8. С++ учебный курс: Учебник. /Франка П. – СПб.:Питер 2005.
9. МОДЕЛИ И CТРУКТУРЫ ДАННЫХ:/ Учебное пособие/
Д.Далека, А.С. Деревянко, О.Г. Кравец, Л.Е. Тимановская -Харьков:ХГПУ, 2000
10.Высшая математика для экономистов: учебник для студентов вузов/Н.Ш.Кремер,3-е издание.-М.:ЮНИТИ-ДАНА,2006
Похожие работы
... треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода. Целью данной курсовой работы является численное решение системы линейных уравнений с помощью метода исключения Гаусса с выбором главного элемента по столбцу. 1 Постановка задачи Задача ставится следующим образом. Пусть требуется найти решение системы линейных алгебраических уравнений a1,1x1 + a1, ...
... 1.2 0.4 -0.8 -0.8 3.6 4 4.7 10.4 9.7 9.7 -8.4Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = ...
... , придумать “свой метод", догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д. Если работа в поисках более рациональный способ решения систем линейных уравнений с двумя переменными - методом подстановки будет успешна, то практическая значимость будет очевидна. Список использованной литературы 1. Алгебра 8 класс. Н.Я. Виленкин. Москва, ...
... 10.4 9.7 9.7 -8.4 Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = b1 , a21x2 + ...
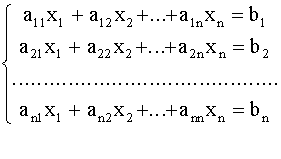
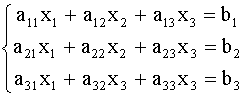



0 комментариев