Навигация
1. Задача классификации.
 |
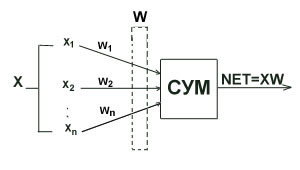
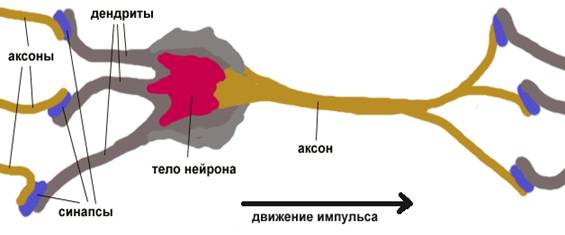
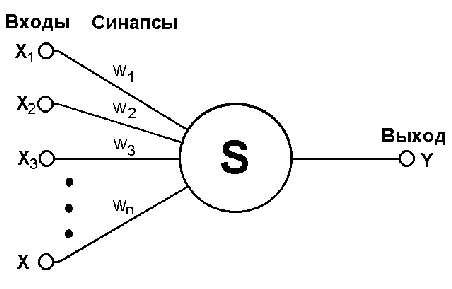
Рассмотрим более подробно, что делает один формальный нейрон в самом простом случае, когда его функцией активации является ступенька.
Рис. 5. Нейрон с пороговой функцией активации разделяет пространство входов гиперплоскостью на две части.
Он дает на выходе 1 если ![]() и 0 если
и 0 если ![]() . Таким образом, он разбивает пространство входов на две части с помощью некоторой гиперплоскости. Если у нас всего два входа, то это пространство двухмерно и нейрон будет разбивать его с помощью прямой линии. Это разбиение определяется весовыми коэффициентами
. Таким образом, он разбивает пространство входов на две части с помощью некоторой гиперплоскости. Если у нас всего два входа, то это пространство двухмерно и нейрон будет разбивать его с помощью прямой линии. Это разбиение определяется весовыми коэффициентами ![]() нейрона.
нейрона.
 |
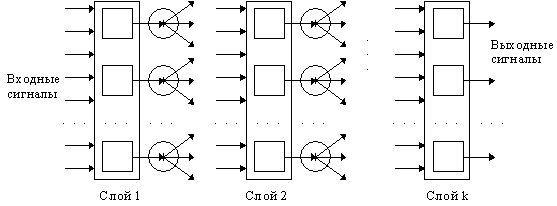
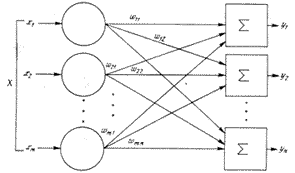
Если мы теперь составим из N таких нейронов слой, то получим разбиение пространства входов N гиперплоскостями. Каждой области в этом пространстве будет соответствовать некий набор нулей и единиц, формирующийся на выходе нашего слоя.
Рис. 6. Кошка, характеризуемая ее линейными размерами.
Таким образом, такая нейронная сеть пригодна для решения задачи многомерной классификации или распознавания образов. Допустим у нас есть некий объект, имеющий набор свойств ![]() . Это может быть, скажем, кошка, характеризуемая ее линейными размерами. Мы можем подать эти параметры на вход нашей сети и сказать, что определенная комбинация нулей и единиц на выходе соответствует объекту «кошка». Таким образом, наша сеть способна выполнять операцию распознавания.
. Это может быть, скажем, кошка, характеризуемая ее линейными размерами. Мы можем подать эти параметры на вход нашей сети и сказать, что определенная комбинация нулей и единиц на выходе соответствует объекту «кошка». Таким образом, наша сеть способна выполнять операцию распознавания.
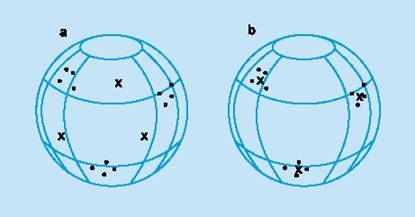
Рис. 7. Простая задача распознавания – линейно разделимые множества.
 |
Однако очевидно, что не для всякой задачи распознавания, существует однослойная сеть ее решающая. Хорошо, если у нас, например, стоит задача различения кошек и собак, причем распределение точек в пространстве параметров такое, как показано на рисунке, когда достаточно провести одну линию (или гиперплоскость) чтобы разделить эти два множества. Тут достаточно одного нейрона.
 |
В более общем случае такое невозможно, например, как на рис.7. В этом случае мы можем использовать слой нейронов, но одному множеству (скажем, кошка) будет соответствовать уже не одна, а множество комбинаций нулей и единиц.
Рис. 8. Задача распознавания с линейно неразделимыми множествами.
Если мы теперь выходы нашего первого слоя нейронов используем в качестве входов для нейронов второго слоя, то нетрудно убедиться, что каждая комбинация нулей и единиц на выходе второго слоя может соответствовать некоему объединению, пересечению и инверсии областей, на которые пространство входов разбивалось первым слоем нейронов. Двухслойная сеть, таким образом, может выделять в пространстве входов произвольные выпуклые односвязные области.
В случае еще более сложной задачи, когда требуется различать многосвязные области произвольной формы, всегда достаточно трехслойной сети.
Мы видим, что нейронные сети с пороговыми функциями активации способны решить произвольную задачу многомерной классификации.
2. Аппроксимация функций.
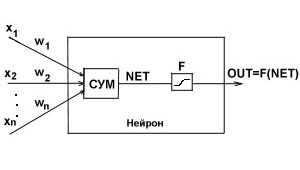
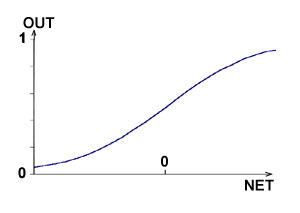
Вторая задача, которую мы рассмотрим это задача аппроксимации функций. Рассмотрим теперь сеть, нейроны которой в качестве функции активации имеют не ступеньку, а некоторую непрерывную функцию, например, сигмоид. В этом случае выход сети будет некоторой непрерывной функцией ее входов. Конкретный вид этой функции определяется весовыми коэффициентами каждого из нейронов.
Возникает вопрос, какие функции могут быть аппроксимированы с помощью нейронной сети? Ответ дается обобщенной теоремой Стоуна. Не вдаваясь в математические тонкости ее можно интерпретировать как утверждение об универсальных аппроксимационных возможностях произвольной нелинейности: с помощью линейных операций и каскадного соединения можно из произвольного нелинейного элемента получить устройство, вычисляющее любую непрерывную функцию с любой наперед заданной точностью.
То есть нейросеть с произвольной функцией активации может аппроксимировать произвольную непрерывную функцию. При этом, как оказывается всегда достаточно трехслойной сети. Нужна большая точность – просто добавь нейронов.
Как частный случай задачи аппроксимации можно рассмотреть задачу предсказания временных рядов. На вход сети мы подаем некоторое количество предыдущих значений, затем, а на выходе ожидаем получить значение в следующий момент времени.
Мы рассмотрели некоторые возможности только многослойных сетей прямого распространения. Ясно, что они могут практически все, что угодно. Возникает вопрос, как подобрать такие весовые коэффициенты, чтобы сеть решала задачу распознавания или аппроксимировала некоторую функцию? Замечательное свойство нейронных сетей состоит в том, что их этому можно научить.
Алгоритмы обучения бывают 3-х видов:
Обучение с учителем. При этом сети предъявляется набор обучающих примеров. Каждый обучающий пример представляют собой пару: вектор входных значений и желаемый выход сети. Скажем, для обучения предсказанию временных рядов это может быть набор нескольких последовательных значений ряда и известное значение в следующий момент времени. В ходе обучения весовые коэффициенты подбираются таким образом, чтобы по этим входам давать выходы максимально близкие к правильным.
Обучение с поощрением. При этом сети не указывается точное значение желаемого выхода, однако, ей выставляется оценка хорошо она поработала или плохо.
Обучение без учителя. Сети предъявляются некоторые входные векторы и в ходе их обработки в ней происходят некоторые процессы самоорганизации, приводящие к тому, что сеть становиться способной решать какую-то задачу.
Рассмотрим один из самых популярных алгоритмов обучения, так называемы, алгоритм обратного распространения. Это один из вариантов обучения с учителем. Пусть у нас имеется многослойная сеть прямого распространения со случайными весовыми коэффициентами. Есть некоторое обучающее множество, состоящее из пар вход сети – желаемый выход ![]() . Через Y обозначим реальное выходное значение нашей сети, которое в начале практически случайно из-за случайности весовых коэффициентов.
. Через Y обозначим реальное выходное значение нашей сети, которое в начале практически случайно из-за случайности весовых коэффициентов.
Обучение состоит в том, чтобы подобрать весовые коэффициенты таким образом, чтобы минимизировать некоторую целевую функцию. В качестве целевой функции рассмотрим сумму квадратов ошибок сети на примерах из обучающего множества.
![]() (6)
(6)
где ![]() реальный выход N-го выходного слоя сети для p-го нейрона на j-м обучающем примере,
реальный выход N-го выходного слоя сети для p-го нейрона на j-м обучающем примере, ![]() желаемый выход. То есть, минимизировав такой функционал, мы получим решение по методу наименьших квадратов.
желаемый выход. То есть, минимизировав такой функционал, мы получим решение по методу наименьших квадратов.
Поскольку весовые коэффициенты в зависимость ![]() входят нелинейно, воспользуемся для нахождения минимума методом наискорейшего спуска. То есть на каждом шаге обучения будем изменять весовые коэффициенты по формуле
входят нелинейно, воспользуемся для нахождения минимума методом наискорейшего спуска. То есть на каждом шаге обучения будем изменять весовые коэффициенты по формуле
 (7)
(7)
где ![]() весовой коэффициент j-го нейрона n-го слоя для связи с i-м нейроном (n-1) - го слоя. Параметр
весовой коэффициент j-го нейрона n-го слоя для связи с i-м нейроном (n-1) - го слоя. Параметр ![]() называется параметром скорости обучения.
называется параметром скорости обучения.
Таким образом, требуется определить частные производные целевой функции E по всем весовым коэффициентам сети. Согласно правилам дифференцирования сложной функции
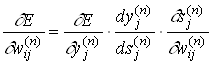 (8)
(8)
где ![]() - выход, а
- выход, а ![]() - взвешенная сума входов j-го нейрона n-го слоя. Заметим, что, зная функцию активации, мы можем вычислить
- взвешенная сума входов j-го нейрона n-го слоя. Заметим, что, зная функцию активации, мы можем вычислить ![]() . Например, для сигмоида в соответствии с формулой (5) эта величина будет равняться
. Например, для сигмоида в соответствии с формулой (5) эта величина будет равняться
 . (9)
. (9)
Третий сомножитель ![]() /
/![]() есть ни что иное, как выход i-го нейрона (n-1) - го слоя, то есть
есть ни что иное, как выход i-го нейрона (n-1) - го слоя, то есть
 . (10)
. (10)
Частные производные целевой функции по весам нейронов выходного слоя теперь можно легко вычислить. Производя дифференцирование (6) по ![]() и учитывая (8) и (10) будем иметь
и учитывая (8) и (10) будем иметь
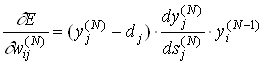 (11)
(11)
Введем обозначение
 . (12)
. (12)
Тогда для нейронов выходного слоя
 . (13)
. (13)
Для весовых коэффициентов нейронов внутренних слоев мы не можем сразу записать, чему равен 1-й сомножитель из (9), однако его можно представить следующим образом:
 (14)
(14)
Заметим, что в этой формуле 1-е два сомножителя есть не что иное, как ![]() . Таким образом, с помощью (14) можно выражать величины
. Таким образом, с помощью (14) можно выражать величины ![]() для нейронов n-го слоя через
для нейронов n-го слоя через ![]() для нейронов (n+1) - го. Поскольку для последнего слоя
для нейронов (n+1) - го. Поскольку для последнего слоя ![]() легко вычисляется по (13), то можно с помощью рекурсивной формулы
легко вычисляется по (13), то можно с помощью рекурсивной формулы
 (15)
(15)
получить значения ![]() для вех нейронов всех слоев.
для вех нейронов всех слоев.
Окончательно формулу (7) для модификации весовых коэффициентов можно записать в виде
![]() . (16)
. (16)
Таким образом, полный алгоритм обучения нейронной сети с помощью алгоритма обратного распространения строиться следующим образом.
Присваиваем всем весовым коэффициентам сети случайные начальные значения. При этом сеть будет осуществлять какое-то случайное преобразование входных сигналов и значения целевой функции (6) будут велики.
Подать на вход сети один из входных векторов из обучающего множества. Вычислить выходные значения сети, запоминая при этом выходные значения каждого из нейронов.
Рассчитать по формуле (13) ![]() . Затем с помощью рекурсивной формулы (15) подсчитываются все остальные
. Затем с помощью рекурсивной формулы (15) подсчитываются все остальные ![]() и, наконец, с помощью (16) изменение весовых коэффициентов сети.
и, наконец, с помощью (16) изменение весовых коэффициентов сети.
Скорректировать веса сети:
![]() .
.
Рассчитать целевую функцию (6). Если она достаточно мала, считаем сеть успешно обучившейся. Иначе возвращаемся на шаг 2.
Перечислим некоторые проблемы, возникающие при применении этого метода.
Локальные минимумыАлгоритм обратного распространения реализует градиентный спуск по поверхности ошибки в пространстве весовых коэффициентов и поэтому может застревать в локальных минимумах. При этом рядом может иметься другой, значительно более глубокий минимум.
Для преодоления этой трудности обучение сети проводят несколько раз и затем выбирают тот вариант обученной сети, который дает наилучшие результаты. Другой метод заключается в том, что сеть можно вывести из локального минимума, на короткое время, увеличив скорость обучения. Иногда, к изменению весовых коэффициентов, вычисленному по алгоритму, добавляют шум. Это также позволяет сети «выпрыгивать» из локальных минимумов.
Паралич сетиВ процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших аргументах функции активации ![]() , в области, где производная функции очень мала (как, например для сигмоидной функции активации). Так как величина коррекции весов пропорциональна этой производной, то процесс обучения может практически замереть. Для преодоления такой ситуации существуют модификации алгоритма, учитывающие лишь направление антиградиента и не учитывающие его величину.
, в области, где производная функции очень мала (как, например для сигмоидной функции активации). Так как величина коррекции весов пропорциональна этой производной, то процесс обучения может практически замереть. Для преодоления такой ситуации существуют модификации алгоритма, учитывающие лишь направление антиградиента и не учитывающие его величину.
Таким образом, мы подробно рассмотрели один из нейронных сетей. Разобрали задачи, решаемые такими сетями (многомерная классификация, аппроксимация функций). Получили один из алгоритмов обучения такой сети. Разумеется, это все лишь малая часть того обширного направления, которое представляют собой нейронные сети.
Хотя многие задачи успешно решаются с помощью нейронных сетей, нужно понимать, что путь от нынешнего состояния работ в этой области к глубокому пониманию принципов работы мозга, по-видимому, очень длинен. Модели в виде нейросетей скорее отвечают на вопрос, как могли бы работать те или иные системы, в каких-то чертах согласующиеся с данными об архитектуре, функциях и особенностях мозга. Тем ни менее исследования в нейронауке уже открыли пути для создания новых компьютерных архитектур и наделению вычислительных систем своеобразной интуицией, способностью к обучению и обобщению поступающей информации, то есть возможностями, которые раньше считались прерогативами живых систем.
Похожие работы
... экспертных систем (А. Батуро), а также лекции проф. А.Н. Горбаня по нейронным сетям. Приложение 1. Плакаты для защиты диплома. ТЕХНОЛОГИЯ ИЗВЛЕЧЕНИЯ ЗНАНИЙ ИЗ НЕЙРОННЫХ СЕТЕЙ: ¨ АПРОБАЦИЯ, ¨ ПРОЕКТИРОВАНИЕ ПО, ¨ ИСПОЛЬЗОВАНИЕ В ПСИХОЛИНГВИСТИКЕ ЦЕЛЬ РАБОТЫ ¨ апробация гибкой технологии извлечения ...
... одном из элективных курсов. Выбор естественно-математического профиля, во-первых, определяется целью введения данного курса в школе (расширение научного мировоззрения) и, во-вторых, сложностью темы в математическом аспекте. Глава 2. Содержание обучения технологии нейронных сетей Авторы данной работы предлагают следующее содержание обучения технологии нейронных сетей. Содержание образования ...
... сети, позволяющая реализовать автоматическое изменение числа нейронов в зависимости от потребностей задачи, позволяет не только исследовать, но и контролировать процесс воспитания психологической интуиции искусственных нейронных сетей. - Впервые применена выборочная константа Липшица для оценки необходимой для решения конкретной задачи структуры нейронной сети. Практическая значимость ...
... . Если же задача не может быть сведена ни к одному из известных классов, разработчику приходится решать задачу синтеза новой конфигурации. Проблема синтеза искусственной нейронной сети сильно зависит от задачи, дать общие подробные рекомендации затруднительно. В большинстве случаев оптимальный вариант искусственной нейронной сети получается опытным путем. Искусственные нейронные сети могут быть ...


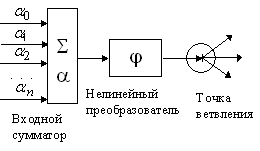




0 комментариев