Навигация
Функционал для градиентного равенства
3. Функционал для градиентного равенства
Функционалом можно считать любую функцию, минимум которой необходимо определить. Вся сложность задачи заключается в ограничениях, накладываемых на переменные и их взаимосвязь. Если ограничения отсутствуют, то говорят о задаче безусловной оптимизации (Пример МНК). К последней сводится и система нелинейных алгебраических уравнений, заданных в неявной форме:
![]()
если из системы сконструировать квадратичный функционал такого вида
![]() ,
,
где ![]() – масштабирующие (весовые) коэффициенты.
– масштабирующие (весовые) коэффициенты.
Подстановка функционала в покомпонентную систему градиентных уравнений приводит к итерационной процедуре с вычислением на каждом шаге следующих выражений:

Если система уравнений линейная, то частные производные ![]() будут константами
будут константами ![]() . Вместе с
. Вместе с ![]() =
=![]() они определяют индивидуальный весовой коэффициент каждого уравнения исходной линейной системы в формулах градиентной итерационной процедуры.
они определяют индивидуальный весовой коэффициент каждого уравнения исходной линейной системы в формулах градиентной итерационной процедуры.
Для нелинейной системы, функционал которой в окрестности точки минимума ![]() можно аппроксимировать квадратичной функцией с положительно определенной матрицей Гессе, в итерационном выражении
можно аппроксимировать квадратичной функцией с положительно определенной матрицей Гессе, в итерационном выражении
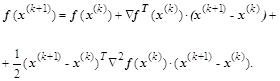
![]() и после приравнивания оставшихся слагаемых нулю и сокращения суммы на вектор
и после приравнивания оставшихся слагаемых нулю и сокращения суммы на вектор ![]() несложно получить соотношение
несложно получить соотношение
![]() ,
,
которое приводит к итерационной формуле
![]()
идентичной формуле Ньютона в применении к решению системы нелинейных уравнений
![]() .
.
Для строго выпуклой, квадратичной функции решение получается за одну итерацию. Этот момент особенно привлекателен для задач линейного программирования, когда целевая функция линейная или квадратичная, а ограничения представлены системой линейных равенств и неравенств. При этом системы равенств и неравенств вводят в общий функционал в виде суммы квадратов функций невязок (аддитивно).
4. Функционалы в задачах условной оптимизации
Конструирование выпуклого квадратичного функционала с учетом ограничений рассмотрим для следующей задачи:

В приведенную обобщенную запись задачи минимизации включены:
Минимизируемая функция вектора искомых параметров (функция цели или критериальная функция):
f(x), ![]() .
.
Система ограничений типа равенств:
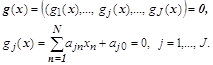
Система ограничений типа неравенств:
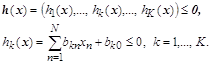
Ограничения на изменения самих неизвестных параметров
![]() ,
,
которые в принципе являются частным случаем ограничений типа неравенств ![]() при
при ![]() , кроме
, кроме ![]() и
и ![]() , задающего границы изменения конкретного параметра:
, задающего границы изменения конкретного параметра:

В качестве квадратов функций невязок для ограничений типа равенств берутся квадраты исходных равенств, умноженные на выравнивающие масштабирующие коэффициенты, которые позволят каждой невязке вносить в общий функционал одно-порядковые приращения при подстановке в него вектора неизвестных:
![]() , j=1, 2, ... ,J.
, j=1, 2, ... ,J.
Систему неравенств необходимо предварительно преобразовать в систему равенств путем умножения ее на единичную (знаковую) функцию
![]()
![]()
Теперь система квадратов невязок для неравенств будет представлена в виде квадратов следующих функций
![]() .
.
Аналогично вводятся квадраты невязок и для ограничений на параметры снизу и сверху:
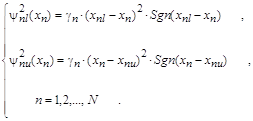
Составной функционал, учитывающий ограничения и требующий минимизации, можно теперь записать в следующем виде:
 .
.
В результате проведенных преобразований исходная задача сведена к задаче безусловной оптимизации и, применяя метод наискорейшего спуска, систему покомпонентных градиентных уравнений получим в виде:
![]()
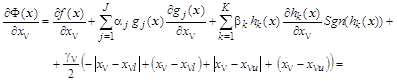
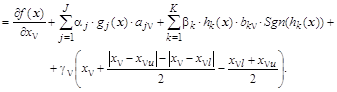
Выражение для ![]() в больших круглых скобках задает кривую с зоной нечувствительности для
в больших круглых скобках задает кривую с зоной нечувствительности для ![]() в интервале
в интервале ![]() . В этом интервале выражение в скобках равно нулю, а вне интервала - пропорционально
. В этом интервале выражение в скобках равно нулю, а вне интервала - пропорционально ![]() с коэффициентом
с коэффициентом ![]() . Если ограничения на переменную не вводятся, т.е. ее границы раздвинуты от
. Если ограничения на переменную не вводятся, т.е. ее границы раздвинуты от ![]() до
до ![]() , то выражение в скобках будет равно нулю.
, то выражение в скобках будет равно нулю.
Литература
1. Вержбицкий В.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М.: Высш.шк., 2001. - 383с.
2. Рено Н.Н. АЛГОРИТМЫ ЧИСЛЕННЫХ МЕТОДОВ: МЕТОДИЧЕСКОЕ ПОСОБИЕ ДЛЯ ВУЗОВ. Изд-во: "Книжный дом Университет" (КДУ), 2007. – 24с.
3. Самарский А.А. Введение в численные методы Учебное пособие для вузов 3-е изд.,стер. ЛАНЬ, 2005. – 288с.
4. Фаворский А.П., Костомаров Д.П. Вводные лекции по численным методам. Логос, 2006. – 184с.
5. Шуп Т.Е. Прикладные численные методы в физике и технике. М.: Высш. шк., 1990. - 255с.
Похожие работы
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... с помощью двухэтапного метода, совпадает с решением, полученным в среде MS Excel с помощью программной надстройки «Поиск решения». 7. ПРИМЕРЫ ПОСТАНОВОК, ФОРМАЛИЗАЦИИ И РЕШЕНИЯ ПЕРСПЕКТИВНЫХ ОПТИМИЗАЦИОННЫХ УПРАВЛЕНЧЕСКИХ ЗАДАЧ Одним из методов решения задач линейного программирования является графический метод, применяемый для решения тех задач, в которых имеются только две переменные, ...
... оптимумам, и именно его ищет конструктор. Возможен случай нескольких равных глобальных оптимумов, расположенных в разных частях пространства проектирования. Как ставится задача оптимизации, лучше всего показать на примере. 2. Методы многомерного поиска На первый взгляд может показаться, что различие между методами многомерного и одномерного поиска состоит лишь в том, что первые требуют ...
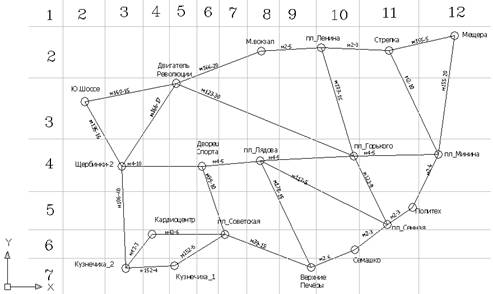
... данных Решение задачи - нахождение оптимального пути Вывод найденного решения 2. Руководство пользователя 2.1 Назначение программы Программа предназначена для поиска оптимального пути в Нижнем Новгороде на маршрутном такси. Или поиск пути в графе, где вершины графа - это остановки, а ветви - участки пути маршрутного такси. С помощью этой программы можно отыскать путь за минимальное ...
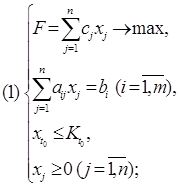
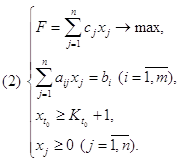

0 комментариев