Навигация
Представление переключательной функции в виде полинома Жегалкина
2. Представление переключательной функции в виде полинома Жегалкина.
Теорема Жегалкина. Любая переключательная функция может быть представлена в виде полинома (многочлена), т. е. записана в форме
f(x1, . . . , xn) = аоÅ a1x1 Å a2x2 Å …Å anxn Å an+1x1 x2Å … Å aNx1…xn ,
(1)
где a0, a1x1, … aN — константы, равные нулю или единице;
Å —операция сложения по модулю два.
При записи конкретной переключательной функции в виде многочлена коэффициенты a0, a1x1, … aN выпадают, так как члены, при которых коэффициенты равны нулю, можно опустить, а коэффициенты, равные единице, не писать.
Для доказательства теоремы Жегалкина предположим, что задана произвольная переключательная функция п аргументов f(x1, . . . , xn), равная единице на некотором числе наборов с номерами m1, … mp.
Покажем, что переключательная функция f(x1, . . . , xn) равна сумме конституент единицы, которые равны единице на тех же наборах, что и данная функция:
f(x1, . . . , xn) = Km1 Å Km2 Å . . . Å Kmp.(2)
Действительно, на каждом из наборов с номерами m1, … mp равна единице только одна конституента, стоящая в правой части выражения (2), а остальные равны нулю. Следовательно, на этих наборах и только на них правая часть выражения (2) принимает значение, равное единице.
Для того чтобы перейти от выражения (2) к виду (1), достаточно представить конституенты единицы в виде произведений и, используя соотношение ![]() , заменить все переменные с отрицаниями (так как отрицания в выражение (3.1) не входят). Пусть например, конституента единицы записана в виде
, заменить все переменные с отрицаниями (так как отрицания в выражение (3.1) не входят). Пусть например, конституента единицы записана в виде
![]() .
.
Тогда получим
Ki= (1 Å x1)x2(1Åx3)x4x5.
Раскрывая скобки и приводя подобные члены в соответствии со свойствами операции сложения по модулю два, получаем запись заданной функции в форме (1), что и доказывает теорему.
Приведенное доказательство теоремы позволяет сформулировать правило представления любой переключательной функции в виде многочлена.
Чтобы переключательную функцию, заданную таблицей истинности, представить в виде полинома Жегалкина, достаточно записать функцию в виде суммы конституент единицы, равных единице на тех же наборах, на которых равна единице заданная функция. Затем все аргументы, входящие в полученное выражение с отрицанием, заменить с помощью соотношения ![]() , раскрыть скобки и привести подобные члены с учетом тождества;
, раскрыть скобки и привести подобные члены с учетом тождества;
![]() x, если п нечетно,
x, если п нечетно,
x Å x Å . . . Å x = 0, если п четно.
Пример 3. Представить в виде полинома Жегалкина функцию f58(x1,x2,x3).
Функция f58(x1,x2,x3) равна единице на втором, третьем, четвертом и шестом наборах, и может быть записана в виде суммы соответствующих конституент единицы:
f58(x1,x2,x3) =K2Å K3Å K4Å K6 =![]() .
.
Используя соотношение ![]() , получаем
, получаем
f58(x1,x2,x3)=(1Åx1)x2(1Åx3)Å(1Åx1)x2x3Å x1(1Åx2)(1Åx3)Åx1x2(1Åx3).
Приводя подобные члены, окончательно находим
f58(x1,x2,x3)= x1Å x2Å x1x2Åx1x3.
3. Совершенная дизъюнктивная нормальная форма переключательной функции.
В общем виде переключательная функция п аргументов может быть задана таблицей истинности. Обозначим через f(i) (i=0, … ,2n-1) значение функции на i-м наборе аргументов. Напомним, что каждая из величин f(i) принимает значение нуль или единица. В соответствие i-му набору аргументов можно поставить конституенту единицы Ki, которая принимает значение, равное единице только на данном f(i)наборе. Умножим каждую конституенту единицы Ki на значение функции f(i) и рассмотрим дизъюнкцию произведений fiKi:
 . (3)
. (3)
Если подставить в выражение (3) значения f(i), то получим дизъюнкцию конституент, которые равны единице на тех же наборах, что и заданная функция. Действительно, ввиду того, что 0×x=0 и 0Úх=х, члены выражения (2), в которых коэффициенты f(i)=0, можно опустить, а так как x×1 = x, то коэффициенты f(i)=1 можно не писать. Тогда
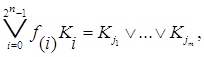
где j1, …,jm – номера наборов, на которых функция равна единице;
m – число таких наборов.
Определение 3. Дизъюнкция конституент единицы, равных единице на тех же наборах, что и заданная функция, называется совершенной дизъюнктивной нормальной формой переключательной функции.
Любую переключательную функцию f(x1, . . . , xn) (кроме константы ноль) можно представить в совершенной дизъюнктивной нормальной форме. Заметим, что любая переключательная функция имеет единственную совершенную дизъюнктивную нормальную форм у: это непосредственно следует из выражения (3).
Совершенную дизъюнктивную нормальную форму переключательной функции удобно находить в такой последовательности:
· выписать ряд произведений всех аргументов и соединить их знаками дизъюнкции; количество произведений должно равняться числу наборов, на которых заданная функция обращается в единицу;
· записать под каждым произведением набор аргументов, на котором функция равна единице, и над аргументами, равными нулю, поставить знаки отрицания.
Это правило называют иногда правилом записи переключательной функции по единицам.
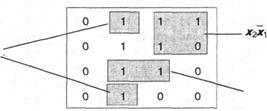
Пример 4. Представить в совершенной дизъюнктивной нормальной форме переключательную функцию четырех аргументов f23805(x1,x2,x3,x4) (см. табл. 2).
Решение. Из табл. 2 видно, что переключательная функция принимает значения, равные единице, на следующих наборах аргументов:
0001, 0011, 0100, 0101, 1000, 1001, 1010, 1011, 1100, 1101, 1111.
Таким образом, совершенная дизъюнктивная нормальная форма функции f23805(x1,x2,x3,x4) будет состоять из одиннадцати дизъюнкций, каждая из которых представляет собой конъюнкцию четырех элементов:
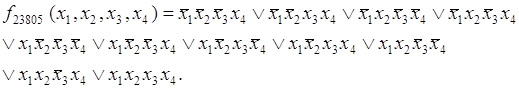
4. Совершенная конъюнктивная нормальная форма переключательной функции.
Если заданная переключательная функция равна единице на большинстве наборов аргументов, то представление функции в совершенной дизъюнктивной нормальной форме может оказаться достаточно громоздким. В этих случаях удобнее использовать другую форму представления функции – совершенную конъюнктивную нормальную форму. Для представления функций в этой форме используется функция конституенты нуля.
Рассмотрим выражение
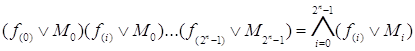 , (4)
, (4)
где f(i) – значение переключательной функции на i-м наборе.
Ввиду справедливости соотношений 1Ú x = 1 и 0Úх= х, при подстановке в выражение (4) значений функции f(i), сомножители, у которых f(i), == 1, можно опустить, а значения функции f(i)=0 не писать. Тогда
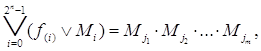 (5)
(5)
где j1, j2, …,jm–номера наборов, на которых функция равна нулю;
т -число таких наборов.
Определение 4. Произведение конституент нуля, которые равны нулю на тех же наборах, что и заданная функция, называется совершенной конъюнктивной нормальной формой.
Любая переключательная функция f(x1, . . . , xn) (кроме константы единицы) может быть представлена в совершенной конъюнктивной нормальной форме. Любая переключательная функция имеет единственную совершенную конъюнктивную нормальную форму.
Сформулируем правило представления переключательной функции в совершенной конъюнктивной нормальной форме. Чтобы представить переключательную функцию п аргументов в совершенной конъюнктивной нормальной форме, достаточно:
· выписать произведение дизъюнкций всех аргументов с количеством сомножителей, равным числу наборов, на которых заданная функция обращается в нуль;
· выписать под каждым сомножителем набор аргументов, на котором функция равна нулю, и над аргументами, равными единице, поставить знаки отрицания;
Это правило иногда называют правилом записи переключательной функции по нулям.
Пример 5. Представить в совершенной конъюнктивной нормальной форме функцию f23805(x1,x2,x3,x4) (см. табл. 2).
Решение. Из табл. 2 видно, что переключательная функция принимает значения, равные нулю, на следующих наборах аргументов:
0000, 0010, 0110, 0111, 1110.
Таким образом, совершенная конъюнктивная нормальная форма функции f23805(x1,x2,x3,x4) будет состоять из пяти конъюнкций, каждая из которых представляет собой дизъюнкцию четырех элементов:
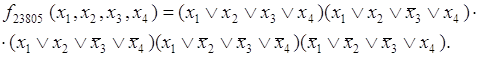
ЛИТЕРАТУРА
1. Белоусов А.И., Ткачев С.Б. Дискретная математика: Учебник для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.– М.: изд-во МГТУ им. Н.Э. Баумана, 2001.– 744 с. (Сер. Математика в техническом университете; Вып XIX).
2. Горбатов В.А. Фундаментальные основы дискретной математики. Информационная математика.– М.: Наука, Физматлит, 2000.– 544 с.– ISBN 5-02-015238-2.
3. Зарубин В.С. Математическое моделирование в технике: Учеб. для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.– М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.– 496 с. (Сер. Математика в техническом университете; вып. XXI, заключительный).
Похожие работы
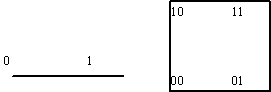
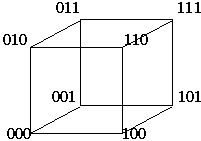
... значения, получим геометрическое представление функции. Например, булева функция, заданная табл.1, геометрически представляется 3-мерным кубом (рис. 1.в). а) n=1 б) n=2 в) n=3 Рисунок 1- Геометрическое задание булевой функции: а) одной переменной: б) двух переменных; в) трех переменных. При аналитическом способе булева функция задается формулами, т. е. аналитическими выражениями, ...
... схемами с односторонней проводимостью, имеющими конечное число входов и один выход. Простейшие электронные схемы, реализующие элементарные булевы функции (НЕ, И, ИЛИ, ИЛИ-НЕ, И-НЕ), называются логическими элементами (ЛЭ). Аналитическая форма представления булевых функций При решении конкретных технических задач булевы функции, отражающие логические связи, наиболее часто задаются в табличной ...
... — f(x1,x2,x3,x4) = 3-йэтап—f(x1,x2,x3,x4)= что и требовалось получить. Проверить правильность проведенных преобразований можно при помощи правила склеивания. 3. Функционально полные системы логических функций. Анализ принадлежности переключательных функций замкнутым классам показывает, что существуют две переключательные функции f8 и f14, не принадлежащие ни одному классу. Согласно теореме ...
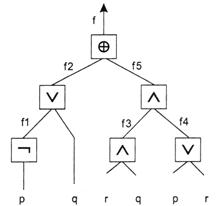
... ответ на этот вопрос положителен. Штрих Шеффера является отрицанием конъюнкции, стрелка Пирса – отрицание дизъюнкции, сумма Жегалкина – отрицание эквивалентности. М. Жегалкин (1869–1947) – российский математик и логик, один из основоположников современной математической логики. Чарльз Пирс (1839–1914) – американский логик, математик и естествоиспытатель. Основоположник семиотики, родоначальник ...


0 комментариев