Навигация
Минимальные формы булевых многочленов
1.3 Минимальные формы булевых многочленов
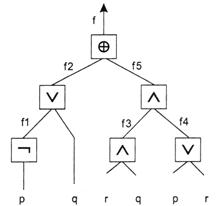
Определение. Понятие булева многочлена определяется рекурсивно. Пусть Хn= {x1,…, xn} – множество из n символов (называемых неизвестными или переменными), которое не содержит символов 0 и 1. Булевы многочлены над Хn суть объекты, которые могут быть получены последовательным применением следующих правил:
(I) х1, х2, …, хn, 0,1 – булевы многочлены;
(II) если p и q – булевы многочлены, то таковыми являются и
(p) Ù (q), (p) Ú (q), (p)¢.
Обозначим множество всех булевых многочленов над Хnчерез Рn.
Пример. Вот несколько примеров булевых многочленов над {х1, х2}: 0,1, х1, х2, х1 Ù х2, х1 Ú х2, х1¢,х1¢ Ù х2.
Так как любой булев многочлен над x1,…, xn модно рассматривать как булев многочлен над x1,…, xn, xn+1, мы имеем
Р1Ì Р2 Ì… Ì РnÌ Рn+1 Ì…
Булев многочлен можно упростить с помощью аксиом булевой алгебры. В процессе упрощения часто трудно решить, какие аксиомы и в каком порядке должны быть использованы. Но существуют некоторые систематические методы упрощения булевых многочленов. Недостатком большинства этих методов является возможность их практического внедрения, когда число переменных слишком велико. Соответствующая проблематика в теории булевых алгебр носит общее название проблема оптимизации или минимизации булевых многочленов; она важна для таких приложений, как упрощение переключательных схем.
Определение. Назовем литералом любую переменную хi и ее дополнение хi¢, а также 0 и 1. Под произведением понимается произведение нескольких литералов, т.е. булев многочлен, в котором нет знака +. Дизъюнктивным выражением или просто выражением назовем буле многочлен, являющийся суммой произведений. Слагаемые в таком выражении назовем дизъюнктами.
Обсуждая упрощение булевых многочленов, мы ограничимся важным случаем сведения дизъюнктивных выражений к «минимальным выражениям» относительно специального условия минимальности. Обозначим через df общее число литералов в выражении f, а через ef – число дизъюнктов. Мы говорим, что выражение f проще выражения j, если df£ dg, ef £ eg и хотя бы одно из этих неравенств строгое. Выражение f называется минимальным, если не существует выражения, которое было бы эквивалентно f и проще f. Таким образом, мы будем искать «кратчайшее» выражение с наименьшим возможным числом литералов, которое было бы эквивалентно f. Такое минимальное выражение не всегда определено однозначно. Я опишу один из нескольких существующих методов упрощения. Он основан на работе Куайна и был улучшен Мак-Класки, поэтому называется методом Куайна - Мак-Класки.
Определение. многочлен p влечет многочлен q, если для любых b1,…., bnÎ В
рв (b1, …, bn) = 1 влечет qв (b1, …, bn) = 1;
в этом случае р называется импликантом для q. Простым импликантом многочлена р называется произведение ![]() , которое влечет р, но если в
, которое влечет р, но если в ![]() вычеркнуть хотя бы один сомножитель, то результат уже не влечет р. Произведение, сомножители-литералы которого образуют подмножество сомножителей-литералов другого произведения, называется подпроизведением последнего.
вычеркнуть хотя бы один сомножитель, то результат уже не влечет р. Произведение, сомножители-литералы которого образуют подмножество сомножителей-литералов другого произведения, называется подпроизведением последнего.
Пример. Произведение х1х3 является подпроизведением как х1х2х3, так и х1х2¢х3, и влечет выражение
![]()
![]() р = х1х2х3 + х1х2¢х3 + х1¢х2¢х3¢,
р = х1х2х3 + х1х2¢х3 + х1¢х2¢х3¢,
![]()
![]() поскольку (х1х3)(1, i2, 1) = 1 и р(1, i2, 1) = 1, а для других значений аргументов х1х3 дает 0. Ни х1, ни х3 не влекут р; например, х1(1, 1, 0) = 1, но р(1, 1, 0) = 0, поэтому х1х3– простой импликант для р.
поскольку (х1х3)(1, i2, 1) = 1 и р(1, i2, 1) = 1, а для других значений аргументов х1х3 дает 0. Ни х1, ни х3 не влекут р; например, х1(1, 1, 0) = 1, но р(1, 1, 0) = 0, поэтому х1х3– простой импликант для р.
Теорема. Любой многочлен р Î Pn эквивалентен сумме всех своих простых импликантов.
Выражение, являющееся суммой простых импликантов для р, называется неприводимым, если оно эквивалентно р, но пересекает быть таковым, если удалить хотя бы одно слагаемое. Минимальное выражение должно быть неприводимым. Поэтому, чтобы определить минимальное выражение, мы находим все неприводимые выражения, а среди них ищем выражение с наименьшим числом литералов. Изложим теперь принадлежащий Куайну метод определения простых импликантов.
Простые импликанты получаются из дизъюнктивной нормальной формы d булева многочлена р применением (слева направо) правила
yz + yz¢ ~ y,
когда это возможно. Более общо, мы используем правило
![]() (*)
(*)
где ![]() и
и ![]() - произведения. следующий пример поможет понять смысл описываемой процедуры.
- произведения. следующий пример поможет понять смысл описываемой процедуры.
Пример. Пусть р – булев многочлен, имеющий следующую дизъюнктивную нормальную форму:
d = wxyz’ + wxy’z’ + wx’yz + wx’yz’ + w’x’yz + w’x’yz’ + w’x’y’z
Мы используем правило ![]() и законы идемпотентности для тех (из общего числа (
и законы идемпотентности для тех (из общего числа (![]() ) = 21) пар дизъюнктов в d, для которых это возможно, тем самым «укорачивая» произведения. например, превый и второй дизъюнкты при использовании (*) дают wxz’. Если в процессе упрощения слагаемые используются хотя бы один раз, то оно помечается. Так как знак + стоит вместо Ú, выражение может быть использовано любое число раз, но помечается не более одного раза. Таким образом, все помеченные произведения содержат более короткие произведения и поэтому не могут быть простыми импликантами. В целом в первом раунде этого процесса мы переходим
) = 21) пар дизъюнктов в d, для которых это возможно, тем самым «укорачивая» произведения. например, превый и второй дизъюнкты при использовании (*) дают wxz’. Если в процессе упрощения слагаемые используются хотя бы один раз, то оно помечается. Так как знак + стоит вместо Ú, выражение может быть использовано любое число раз, но помечается не более одного раза. Таким образом, все помеченные произведения содержат более короткие произведения и поэтому не могут быть простыми импликантами. В целом в первом раунде этого процесса мы переходим
от wxyz’ и wxy’z’ к wxz’
от wx’yz и wx’yz’ к wx’y
от wxyz’ и wx’yz’ к wyz’
от w’x’yz и w’x’yz’ к w’x’y
от w’x’yz и w’x’y’z к w’x’z
от wx’yz и w’x’yz к x’yz
от wx’yz’ и w’x’yz’ к x’yz’
Здесь использованы, и потому должны быть помечены, все семь слагаемых.
В общем, эта процедура повторяется снова и снова с использованием только помеченных выражений (которые становятся короче). Прочие произведения суть простые импликанты и остаются неизменными.
В нашем примере второй раунд упрощения осуществляет переход
от wx’y и w’x’y к x’y
от x’yz и x’yz’ к x’y
Четыре выражения - wx’y, w’x’y, x’yz, x’yz’ – помечены. Остальные произведения, а именно wxz’, wyz’, w’x’z не могут быть упрощен. следовательно, р эквивалентно такой сумме простых импликантов:
р ~ wxz’ + wyz’ + w’x’z + x’y.
Как уже было сказано, Мак-Класки улучшил это метод. Чтобы описать улучшенный алгоритм, используем многочлен
d = wxyz’ + wxy’z’ + wx’yz + wx’yz’ + w’x’yz + w’x’yz’ + w’x’y’z
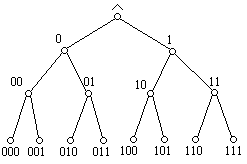
Шаг 1. Считая переменные упорядоченными по алфавиту (или по номерам), поставим в соответствие каждому произведению последовательность символов из {0, 1, -}: вместо xi’ и xiзапишем 0 и 1 соответственно, а вместо опущенных переменных запишем черточку. Например, вместо w’x’y’z запишем 0001, а вместо w’x’z – 00-1.
Шаг 2. Произведения, рассматриваемые как троичные n-ки, разбиваются на классы эквивалентности в соответствии с числом единиц. Упорядочим классы по возрастанию этого числа. В нашем примере:
w’x’y’z0 0 0 1
w’x’yz’0 0 1 0
w’x’yz0 0 1 1
wx’yz’1 0 1 0
wx’yz 1 0 1 1
wxyz’1 1 1 0
wxy’z’1 1 0 0
Шаг 3. Используя правило (*), нужно складывать только произведения из соседних классов, т.е. когда числа единиц в соответствующих последовательностях отличаются лишь на 1. При этом мы должны сравнивать выражения из соседних классов, имеющих черточки в одних и тех же позициях. Если два таких выражения отличаются точно в одной позиции, то они имеют вид р = i1i2…ir…in и q = i1i2…ir’…in, где все ik лежат в {0, 1, -}, а ir лежит в {0, 1}. Тогда (*) сводит p, q к i1i2…ir-1 - ir+1 …in, причем p и q должны быть помечены. В рассматриваемом примере это дает такие четверки (метки относятся к следующему раунду, тогда как в предыдущем списке все произведения следовало пометить):
0 0 - 1
0 0 1 -ü
- 0 1 0ü
- 0 1 1ü
1 0 1 -ü
1 - 1 0
1 1 - 0
Помеченные выражения не являются простыми импликантами и во втором раунде этого шага дают единственное выражение
- 0 1 -
Итак, мы нашли все простые импликанты, а именно
0 0 1 - w’x’z
- 0 1 0 wyz’
- 0 1 1 wxz’
1 0 1 - x’y
Так как сумма всех простых импликантов необязательно является минимальным выражением, алгоритм требует выполнения ещё одного шага.
Шаг 4. В силу теоремы сумма всех простых импликантов для р эквивалентна р. поэтому для каждого слагаемого дизъюнктивной нормальной формы d многочлена р должен существовать простой импликант, являющийся произведением этого слагаемого. для выявления возникшего соответствия удобно использовать таблицу простых импликантов. столбцы этой таблицы индексируются дизъюнктами из d, а строки – простыми импликантами, вычисленными в шаге 3. на пересечении i-й строки и j-го столбца ставится крестик û, если простой импликант из i-й строки является подпроизведением произведения из j-го столбца. Говорят, что одно произведение покрывает, если первое является подпроизведением второго. Для того, чтобы найти сумму простых импликантов, которая будет эквивалентна d , мы из множества всех простых импликантов выбираем подмножество таким образом, чтобы каждое слагаемое в d покрывалось по крайней мере одним импликантом из подмножества. Тогда минимальной формой будет сумма простых импликантов с наименьшим числом членов и наименьшим числом букв. Простой импликант называется главным членом, если он покрывает произведение, не покрываемое никаким другим простым импликантом; сумма всех главных членов называется ядром. сначала мы находим ядро, затем обозначаем через q1,…,qk произведения, не покрываемые простыми импликантами из ядра; простые импликанты, не входящие в ядро, обозначим через р1,…,рm. Далее формируем таблицу, столбцы которой индексируются элементами qi, а строки – элементами рi. Крестик û на месте (i, j) указывает, что рi покрывает qj.
Теперь образуем произведение сумм. Каждый сомножитель соответствует одному из qj и является суммой тех рi, который покрывают этот qj. Используя законы булевой алгебры, мы преобразуем это выражение в простейшую возможную сумму произведений. Каждое из этих произведений представляет подмножество элементов рi, которые покрывают все qj. Далее рассматриваем произведения с наименьшим числом сомножителей. Из этих кратчайших произведений выбираем те, что содержат наименьшее общее число литералов. Теперь каждое из полученных произведений переписываем в виде суммы составляющих его простых импликантов, складываем с ядром, получая минимальную сумму произведений, эквивалентную р.
II.РЕШЕНИЕ МИНИМАЛЬНЫХ ФОРМ БУЛЕВЫХ МНОГОЧЛЕНОВ С ПОМОЩЬЮ МЕТОДА КУАЙНА – МАК-КЛАСКИ
Задача. Определим форму булева многочлена р, заданного в дизъюнктивной нормальной форме
d = v’w’x’y’z’ + v’w’x’yz’ + v’w’xy’z’ + v’w’xyz’ + v’wx’y’z + v’wx’yz’ + v’wxy’z + v’wxyz’ + v’wxyz + vw’x’y’z’ + vw’x’y’z + vw’xy’z + vwx’yz’ + vwxy’z’ + vwxyz’ + vwxyz
Решение:
Шаги 1 и 2
| 0 единиц | 0 0 0 0 0 | ü | (1) |
| 1 единица | 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0 | ü ü ü | (2) (3) (4) |
| 2 единицы | 0 0 1 1 0 0 1 0 0 1 0 1 0 1 0 1 0 0 0 1 | ü ü ü ü | (5) (6) (7) (8) |
| 3 единицы | 0 1 1 0 1 0 1 1 1 0 1 0 1 0 1 1 1 0 1 0 1 1 1 0 0 | ü ü ü ü ü | (9) (10) (11) (12) (13) |
| 4 единицы | 0 1 1 1 1 1 1 1 1 0 | ü ü | (14) (15) |
| 5 единиц | 1 1 1 1 1 | ü | (16) |
Шаг 3. Комбинация строк (i) и (j) дает сокращение, указанное в строке (i)(j):
| (1)(2) (1)(3) (1)(4) | 0 0 0 - 0 0 0 - 0 0 - 0 0 0 0 | ü ü J |
| (2)(5) (2)(7) (3)(5) (4)(8) | 0 0 - 1 0 0 - 0 1 0 0 0 1 - 0 1 0 0 0 - | ü ü ü I |
| (5)(10) (6)(9) (7)(10) (7)(12) (8)(11) | 0 - 1 1 0 0 1 - 0 1 0 1 - 1 0 - 1 0 1 0 1 0 - 0 1 | ü H ü ü G |
| (9)(14) (10)(14) (10)(15) (12)(15) (13)(15) | 0 1 1 - 1 0 1 1 1 - - 1 1 1 0 1 1 -1 0 1 1 1 - 0 | F ü ü ü Е |
| (14)(16) (15)(16) | - 1 1 1 1 1 1 1 1 - | ü ü |
Повторение этого шага с новыми строками дает нам
| (1)(2)(3)(5) | 0 0 - - | D |
| (2)(5)(7)(10) | 0 - - 1 0 | C |
| (7)(10)(12)(15) | - 1 - 1 0 | B |
| (10)(15)(14)(16) | - 1 1 1 - | A |
Пометки «птичкой» ü и буквами сделаны после процесса упрощения. найденные простые импликанты обозначены буквами А, В, …J.
Шаг 4. Формируем таблицу простых импликантов, где индексы столбцов – слагаемые из d – представлены в виде двоичных столбцов.
|
| (1) 0 0 0 0 0 | (2) 0 0 0 1 0 | (3) 0 0 1 0 0 | (4) 1 0 0 0 0 | (5) 0 0 1 1 0 | (6) 0 1 0 0 1 | (7) 0 1 0 1 0 | (8) 1 0 0 0 1 | (9) 0 1 1 0 1 | (10) 0 1 1 1 0 | (11) 1 0 1 0 1 | (12) 1 1 0 1 0 | (13) 1 1 1 0 0 | (14) 0 1 1 1 1 | (15) 1 1 1 1 0 | (16) 1 1 1 1 1 |
| -111- А |
|
|
|
|
|
|
|
|
| û |
|
|
| û | û | û |
| -1-10 В |
|
|
|
|
|
| û |
|
| û |
| û |
|
| û |
|
| 0--10 С |
| û |
|
| û |
| û |
|
| û |
|
|
|
|
|
|
| 00--0 D | û | û | û |
| û |
|
|
|
|
|
|
|
|
|
|
|
| 111-0 E |
|
|
|
|
|
|
|
|
|
|
|
| û |
| û |
|
| 011-1 F |
|
|
|
|
|
|
|
| û |
|
|
|
| û |
|
|
| 10-01 G |
|
|
|
|
|
|
| û |
|
| û |
|
|
|
|
|
| 01-01 H |
|
|
|
|
| û |
|
| û |
|
|
|
|
|
|
|
| 1000- I |
|
|
| û |
|
|
| û |
|
|
|
|
|
|
|
|
| -0000 J | û |
|
| û |
|
|
|
|
|
|
|
|
|
|
|
|
В наших кратких обозначениях ядро, т.е. сумма главных членов, есть D + H + G + B + E + A. Единственным произведение, не покрываемым ядро, является (4); это и есть q1. Простыми импликантами pi, не входящими в ядро, являются С, F, I, J. Новая таблица имеет вид
|
| (4) 1 0 0 0 0 |
| 0 - - 1 0 С |
|
| 0 1 1 - 1 F |
|
| 1 0 0 0 - I | û |
| - 0 0 0 0 J | û |
Это обозначает, что мы получаем две минимальные форы:
(i) D + H + G + B + E + A + I, если использовать I, и
(ii) D + H + G + B + E + A + J, если выбрать J.
В обычных обозначениях минимальная форма (i) такова:
v’w’z’ + v’wy’z + vw’y’z + wyz’ + vwxz’ + wxy + vw’x’y’.
ЗАКЛЮЧЕНИЕ
По результатам проведённого курсового исследования по теме «Минимальные формы булевых многочленов» можно сделать следующие выводы.
При всей простоте своей аксиоматики теория булевых алгебр весьма содержательна. Мы находим в ней немало трудных и глубоких проблем, многие из которых ещё не решены. Эти проблемы весьма разнообразны, они соприкасаются с логикой и теорией множеств, с теорией вероятностей и анализом. Такое обилие точек соприкосновения со смежными математическими дисциплинами роднит теорию булевых алгебр с функциональным анализом, к которому она близка и по своему общему математическому стилю.
Существуют различные методы нахождения минимальных форм булевых многочленов. В своей курсовой работе я исследовала один из методов - метод Куайна - Мак-Класки. Он предназначен для нахождения множества простых импликант для функций, заданных совокупностью наборов, на которых функция равна единице, или дизъюнктивной совершенной нормальной формой. Умение минимизировать логические функции имеет огромное значение при проектировании устройств цифровой электроники.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Владимиров Д.А., Булевы алгебры – М., Издательство «Наука» 1969.
2. Дискретная математика и математические вопросы кибернетики – под общей редакцией С.В. Яблонского и О.Б. Лупанова – М., «Наука», 1974.
3. Лидл Р., Пильц Г., «Прикладная абстрактная алгебра» - Екатеринбург, «Издательство уральского университета» 1996.
4. www.exponenta.ru/educat/systemat/1006/2_tutorials/bin_log.asp
5. www.intuit.ru/department/hardware/archsys/keywords.2.html
Похожие работы
... ответ на этот вопрос положителен. Штрих Шеффера является отрицанием конъюнкции, стрелка Пирса – отрицание дизъюнкции, сумма Жегалкина – отрицание эквивалентности. М. Жегалкин (1869–1947) – российский математик и логик, один из основоположников современной математической логики. Чарльз Пирс (1839–1914) – американский логик, математик и естествоиспытатель. Основоположник семиотики, родоначальник ...
... которым они имели место, является одним из необходимых условий разработки защищенных систем и их использования.АЛГОРИТМ RC4 В настоящей работе проведен анализ криптостойкости методов защиты информации, применяемых в операционных системах семейства Microsoft Windows 95, 98. Кроме того, нами было проведено исследование по поиску необходимой длины ключа и пароля, а также были рассмотрены проблемы ...
... порядке); конструктор (создает объект и инициализирует его состояние); деструктор (разрушает объект и освобождает занимаемую им память). В чистых объектно-ориентированных языках программирования операции могут объявляться только как методы – элементы классов, экземплярами которых являются объекты. Гибридные языки позволяют писать операции как свободные подпрограммы (вне классов). В общем ...
... обучения, yi и yj –выходные сигналы i-го и j-го нейронов. В настоящее время существует множество разнообразных обучающих правил (алгоритмов обучения). Глава IV Может ли компьютер мыслить? 4.1 Реально ли компьютерное мышление? Наконец я подошел к заключительной главе своей работы. В предыдущих главах была изложена сущность построения систем искусственного интеллекта, было рассказано о ...




0 комментариев