Навигация
Первые исследования по демографии
5. Первые исследования по демографии
Одним из толчков для развития основных понятий теории вероятностей сыграли исследования Джона Граунта (1620–1675) и Вильяма Петти (1623–1687) по демографии. Их работы наглядно продемонстрировали, каким мощным орудием могут служить для изучения массовых явлений статистические наблюдения, если их соответствующим образом обработать. Первой работой, с которой начинается история статистики как области научного знания, следует назвать книгу Граунта, опубликованную в 1662 г. под названием «Естественные и политические наблюдения, перечисленные в прилагаемом оглавлении и сделанные над бюллетенями смертности. По отношению к управлению, религии, торговле, росту, воздуху, болезням и разным изменениям означенного города».
Основная задача, которая интересовала Граунта, состояла в указании метода, который позволял бы установить с достаточной точностью возрастной состав населения города в результате наблюдений за возрастом умерших. С этой целью им были проанализированы 229 250 регистраций смертей в Лондоне происшедших за 20 лет. Среди этих смертей было отмечено 71 124 смерти детей от 0 до 6 лет. Причины смертей были тщательно перечислены Граунтом. Он специально отметил, что отношение числа смертей детей от 0 до 6 лет к общему числу смертей за тот же период времени, равное 71 124/229 250, приблизительно равняется 1/3. Иными словами, Граунт ввел представление о частоте события. Для развития теории вероятностей это обстоятельство сыграло огромную роль, как и его замечание: «…мы бы хотели отметить, что некоторые из случайностей имеют постоянное отношение к числу всех похорон». Здесь Граунт вплотную подошел к представлению о статистической устойчивости средних. Им была составлена первая таблица смертности.
Граунт прекрасно понимал, что точность его выводов тем больше, чем больше наблюдений имеется для обработки. Именно в связи с этим он отметил, что недостаточно ограничиваться обработкой бюллетеней смертности только за одну неделю для получения полноценных выводов о составе населения.
Понятие частоты подхватили другие авторы. Так в небольшой книге В. Петти «Два очерка по политической арифметике, относящиеся к людям, зданиям, больницам в Лондоне, Париже», вышедшей в 1682 г. в Лондоне, а через два года во французском переводе в Париже, были даны сравнительные данные о смертности в госпиталях шарите Парижа и Лондона.
Работы Граунта, Петти и ряда их последователей представляют собой ничто иное, как первые шаги в области математической статистики.
Непосредственным продолжателем исследований, начатых Граунтом и Петти, был знаменитый английский астроном Эдмунт Галлей (1656–1742). В 1693 г. Галлей опубликовал в изданиях Лондонского королевского общества две статьи «Оценка степеней смертности человечества, выведенная на основании любопытных таблиц рождений и погребений города Бреславля, с попыткой установить цену пожизненных рент» и «Несколько дальнейших замечаний по поводу Бреславльских бюллетеней смертности». Одна из причин интереса Галлея к таблицам смертности состоит в том, что сами Граунт и Петти сознавали недостаточную обоснованность своих выводов, поскольку у них отсутствовали численность населения и возраст умерших. Кроме того, в городах, которые они изучали, был большой приток населения извне. Это обстоятельство делает указанные города «неподходящими в качестве стандарта для этой цели, которая требует, если это возможно, чтобы население, с которым имеют дело, было совершенно закрытым, т.е. таким, где все умирают там, где они родились, где нет никаких эмигрантов и иммигрантов. По словам Галлея, бреславльские материалы не имеют указанных дефектов.
На основании имевшихся у него данных Галлей составил таблицу смертности, которую он рассматривал одновременно и как таблицу доживающих по возрасту лиц, так и как распределение населения по возрасту. Он ввел в науку понятие о вероятной продолжительности жизни, как о возрасте, которого одинаково можно достигнуть и не достигнуть. На современном языке это медиана длительности жизни. В вычислениях Галлея можно заметить использование им принципов, лежащих в основе теорем сложения т умножения вероятностей, а также рассуждения, близкие к формулировке закона больших чисел.
Работы Галлея имели очень большое значение для развития науки и применений статистических исследований о народонаселении к вопросам страхования.
6. Возникновение классического определения вероятности
До конца 17 в. наука так и не подошла к введению классического определения вероятности. Однако в 30-х годах 18-го столетия классическое определение вероятности стало общеупотребительным, и никто из ученых этих лет не мог бы ограничиться только подсчетом числа благоприятствующих событию шансов. Введение классического определения вероятности произошло не в результате однократного действия, а заняло длительный промежуток времени, на протяжении которого происходило непрерывное совершенствование формулировки, переход от частных задач к общему случаю. Еще в книге Гюйгенса «О расчетах в азартных играх» (1657) нет понятия вероятности как числа, заключенного между 0 и 1 и равного отношению числа благоприятствующих событию шансов к числу всех возможных. А в трактате Я. Бернулли «Искусство предположений» (1713) понятие это введено, хотя и в несовершенной форме. Что же заставило Бернулли ввести в научный обиход классическое понятие вероятности?
Несомненно, что формулировка закона больших чисел, осуществленная Бернулли, сама по себе является достаточным для этого основанием. Однако сильное влияние на ход мыслей ряда исследователей, в том числе и Бернулли, оказали работы Граунта и Петти. Их произведения убедительно показали преимущества понятие частоты перед понятием численности. Понятие частоты, т.е. отношение числа наблюдений, в которых появляется определенное свойство, к числу всех наблюдений, позволяет получить серьезные практические выводы. Отсюда оставался один шаг до введения классического определения вероятности. Выводы Граунта и Петти относительно устойчивости некоторых событий подготовили почву и к формулировке закона больших чисел.
Бернулли дал такое определение вероятности: «Вероятность есть степень достоверности и отличается от нее, как часть от целого». Далее было пояснение сказанного на примере, который показывает, что Бернулли в данную им формулировку вкладывал тот же смысл, какой мы вкладываем в классическое определение вероятности.
Интересны другие рассуждения его работы. Бернулли задал вопрос: как определить вероятность случайного события, если у нас нет возможности подсчитать числа всех возможных и благоприятствующих ему шансов? Ответ был им сформулирован следующим образом: «Но здесь нам открывается другая дорога для достижения искомого. И то, что не дано вывести a priori, то, по крайней мере, можно получить a posteriori, т.е. из многократного наблюдения результатов в подобных примерах… Ибо, если, например, при наблюдениях, сделанных некогда над тремя сотнями людей того же возраста и сложения, в каких находится теперь Тит, было замечено, что из них двести до истечения 10 лет умерли, а остальные остались в живых и дальше, то можно заключить с достаточным основанием, что имеется вдвое больше случаев Титу умереть в течение ближайшего десятилетия, чем остаться в живых по истечении этого срока… Этот опытный способ определения числа случаев по наблюдениям не нов и не необычен».
Важно подчеркнуть, что в высказанных отрывках достаточно четко прослеживается мысль о статистическом определении вероятности. Таким образом, в трактате Бернулли присутствуют обе концепции вероятности классическая и статистическая. Обе они изложены не очень четко, но они уже введены в рассмотрение и использованы. Введено в рассмотрение понятие вероятности случайного события, как числа, заключенного между 0 и 1. Достоверному событию приписывается максимально возможное значение вероятности единица, а невозможному минимальное ноль. Кроме того, было ясно сказано, что это число может быть определено двумя различными способами: путем подсчета числа равновозможных случаев, которые благоприятствуют событию, и всех возможных случаев и вычисления их отношения или же путем проведения большого числа независимых испытаний и вычисления частоты события.
Монмор в своей книге «Обзор анализа азартных игр» использовал введенное Бернулли понятие вероятности и применил его к решению достаточно сложных задач. В частности Монмор рассмотрел и правильно решил следующую задачу: имеется ![]() предметов, пронумерованных числами от 1 до
предметов, пронумерованных числами от 1 до ![]() . Спрашивается, чему равна вероятность того, что при последовательном вынимании этих предметов наудачу (без возвращения) хотя бы один предмет будет вынут так, что номер вынимания совпадет с присвоенным ему номером. Эта вероятность оказалась равной
. Спрашивается, чему равна вероятность того, что при последовательном вынимании этих предметов наудачу (без возвращения) хотя бы один предмет будет вынут так, что номер вынимания совпадет с присвоенным ему номером. Эта вероятность оказалась равной ![]() .
.
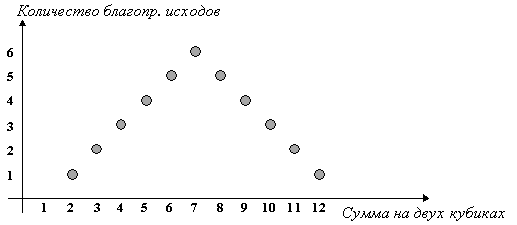
А. Муавр принял классическое определение вероятности, данное Бернулли, и вероятность события определил в точности так, как это делаем мы теперь. Он писал: «Следовательно, мы строим дробь, числитель которой будет число случаев появления события, а знаменатель число всех случаев, при которых оно может появиться или не появиться, такая дробь будет выражать действительную вероятность его появления». Муавр, как и Бернулли не заострял внимание на то, что шансы должны быть равновероятными. Это замечание впервые было введено в определение классической вероятности лишь П. Лапласом в его «Аналитической теории вероятностей». Лагранж об этом еще не задумывался и давал определение вероятности в точности по Муавру. По-видимому, на Лапласа повлияла дискуссия, начатая Д`Аламбером, который при решении задачи о вероятности выпадения (при бросании двух монет) герба на одной из монет и решки на другой, определил ее равной 1/3. Это он мотивировал тем, что имеется лишь три возможности:
1) на обеих монетах выпадает герб;
2) на обеих монетах выпадает решка;
3) на одной монете выпадает герб, а на другой решка.
Похожие работы
... понятия вероятности задача некоторой несостоятельности классического определения вероятности была решена. Однако наблюдаются попытки дать трактовку вероятности с более широких позиций, в том числе и с позиций теории информации. 2. Динамика развития понятия математического ожидания 2.1 Предпосылки введения понятия математического ожидания Одним из первых приблизился к определению понятия ...
... монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку. Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы) Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при ...
... вероятностей совместимых событий; формулы: полной вероятности, Бейеса (Байеса). Одной из форм дифференцированного обучения по курсу теории вероятностей может являться факультативный курс. 2. Разработка программы факультативного курса по теории вероятностей в курсе математики 8 класса 2.1 Основные понятия о факультативном курсе Возможность 1-2 часа в неделю дополнительно работать со ...
... равна 0,515). Конец 19 в. и 1-я половина 20 в. отмечены открытием большого числа статистических закономерностей в физике, химии, биологии и т.п. Возможность применения методов теории вероятностей к изучению статистических закономерностей, относящихся к весьма далёким друг от друга областям науки, основана на том, что вероятности событий всегда удовлетворяют некоторым простым соотношениям, о ...

0 комментариев