Навигация
Критерии согласия для сложной гипотезы
1.3 Критерии согласия для сложной гипотезы
На практике задача о согласии данных наблюдений с некоторым совершенно конкретным распределением, встречается реже, чем задача проверки сложной гипотезы, которую мы рассматриваем ниже.
Более трудной, но более важной для приложений задачей является проверка гипотезы о том, что данная выборка подчиняется определенному параметрическому закону распределения, например нормальному закону. Параметры этого закона остаются неопределенными, так что эта гипотеза сложная.
Пусть x1, …, xn – выборка из распределения с функцией распределения
F(x, ![]() ). Здесь
). Здесь ![]() - неизвестный параметр, не обязательно скалярный.[11] Обозначим его истинное значение через
- неизвестный параметр, не обязательно скалярный.[11] Обозначим его истинное значение через ![]() º. Сейчас мы не можем сравнить выборочную функцию распределения Fn(x) и теоретическую, поскольку эта последняя нам не вполне известна: в ее выражение F(x,
º. Сейчас мы не можем сравнить выборочную функцию распределения Fn(x) и теоретическую, поскольку эта последняя нам не вполне известна: в ее выражение F(x, ![]() º) входит неопределенный параметр
º) входит неопределенный параметр ![]() º. Мы, однако, можем найти для
º. Мы, однако, можем найти для ![]() º приближенное значение, основываясь на выборке x1, …, xn. Для этого можно использовать разные методы оценивания, но наиболее ясные и в определенном смысле наилучшие результаты получаются, если использовать метод наибольшего правдоподобия.
º приближенное значение, основываясь на выборке x1, …, xn. Для этого можно использовать разные методы оценивания, но наиболее ясные и в определенном смысле наилучшие результаты получаются, если использовать метод наибольшего правдоподобия.
Итак, пусть ![]() n – оценка наибольшего правдоподобия по выборке x1, …, xn для неизвестного параметра
n – оценка наибольшего правдоподобия по выборке x1, …, xn для неизвестного параметра ![]() распределения F(x,
распределения F(x, ![]() ). Теперь для вычисления статистики Колмогорова вместо F(x,
). Теперь для вычисления статистики Колмогорова вместо F(x, ![]() º) мы можем использовать F(x,
º) мы можем использовать F(x, ![]() n) и ввести модифицированную статистику Колмогорова:
n) и ввести модифицированную статистику Колмогорова:
![]() (3.1)
(3.1)
Аналогично, модифицированная статистика омега-квадрат есть:
![]() (3.2)
(3.2)
Свойства статистик Dn и ![]() во многом повторяют отмеченные ранее свойства статистик Dn и
во многом повторяют отмеченные ранее свойства статистик Dn и ![]() . В частности,
. В частности, ![]() и n
и n![]() неограниченно возрастают, если проверяемая гипотеза неверна. Поэтому эту гипотезу следует отвергнуть, если наблюденное значение
неограниченно возрастают, если проверяемая гипотеза неверна. Поэтому эту гипотезу следует отвергнуть, если наблюденное значение ![]() (или n
(или n![]() , если применяется модифицированный критерий омега-квадрат) неправдоподобно велико, например, превосходит критическое значение, о котором будет сказано ниже.
, если применяется модифицированный критерий омега-квадрат) неправдоподобно велико, например, превосходит критическое значение, о котором будет сказано ниже.
Важно отметить, что статистика Dn распределена иначе, чем Dn (1.1), а статистика ![]() – иначе, чем
– иначе, чем ![]() (1.5). Причина в том, что из-за подбора
(1.5). Причина в том, что из-за подбора ![]() n по выборке функций F(x) и F(x,
n по выборке функций F(x) и F(x, ![]() n) (в случае, если гипотеза о типе распределения верна) оказываются ближе к друг другу, чем F(x) и F(x,
n) (в случае, если гипотеза о типе распределения верна) оказываются ближе к друг другу, чем F(x) и F(x, ![]() º). Поэтому при справедливости гипотезы статистика Dn, как правило, будет принимать существенно меньше значения, чем Dn. Аналогично соотносятся
º). Поэтому при справедливости гипотезы статистика Dn, как правило, будет принимать существенно меньше значения, чем Dn. Аналогично соотносятся ![]() и
и ![]() .
.
Поскольку статистики (3.1), (3.2) при справедливости гипотезы имеют иные распределения, чем статистики Dn и ![]() , для их применения необходимы таблицы распределений или хотя бы таблицы критических значений. К сожалению, модифицированные статистики (3.1), (3.2) не обладают столь привлекательным свойством «свободы от распределения выборки», как их прототипы, поэтому для каждого параметрического семейства распределений нужны свои таблицы. Более того, распределения (3.1), (3.2) могут зависеть и от истинного значения неизвестного параметра (параметров).[4] К счастью, для так называемых «масштабно-сдвиговых» семейств, к которым относятся нормальные, показательное и многие другие практически важные распределения, этого последнего осложнения не возникает.
, для их применения необходимы таблицы распределений или хотя бы таблицы критических значений. К сожалению, модифицированные статистики (3.1), (3.2) не обладают столь привлекательным свойством «свободы от распределения выборки», как их прототипы, поэтому для каждого параметрического семейства распределений нужны свои таблицы. Более того, распределения (3.1), (3.2) могут зависеть и от истинного значения неизвестного параметра (параметров).[4] К счастью, для так называемых «масштабно-сдвиговых» семейств, к которым относятся нормальные, показательное и многие другие практически важные распределения, этого последнего осложнения не возникает.
Таблицы распределений статистик (3.1), (3.2) к настоящему моменту составлены для многих семейств. Большинство из них рассчитаны методом случайных испытаний (методом Монте-Карло). Автор большинства этих расчетов М. Стефенс заметил, что зависимость результатов от объема выборки резко уменьшается, если вместо Dn , ![]() использовать их несколько преобразованные варианты. Стефенс утверждает, что для этих форм зависимость от n практически перестает сказываться, начиная с n = 5. ниже приводятся некоторые таблицы Стефенса.
использовать их несколько преобразованные варианты. Стефенс утверждает, что для этих форм зависимость от n практически перестает сказываться, начиная с n = 5. ниже приводятся некоторые таблицы Стефенса.
Табл. 3.1 Модифицированные критерии для проверки нормальности, оба параметра неизвестны
| Статистика | Модифицированная форма | Верхние процентные точки 0.15 0.10 0.05 0.025 0.01 |
| Dn |
| 0.775 0.819 0.895 0.955 1.035 |
|
|
| 0.091 0.104 0.126 0.148 0.178 |
Табл. 3.2 Модифицированные критерии для проверки экспоненциальности, параметр неизвестен
| Статистика | Модифицированная форма | Верхние процентные точки 0.15 0.10 0.05 0.025 0.01 |
| Dn |
| 0.926 0.990 1.094 1.190 1.308 |
|
|
| 0.149 0.177 0.224 0.273 0.337 |
Предельное (при n → ∞) распределение n![]() известно, но вычисляется довольно сложно. Предельное распределение для
известно, но вычисляется довольно сложно. Предельное распределение для ![]() найти не удалось, есть лишь приближенные формулы для критических значений, основанные на асимптотических разложениях. Сравнение расчетов по этим формулам с упомянутыми ранее таблицами показало их хорошее согласие. Как уже говорилось, для каждого параметрического семейства критические значения надо рассчитывать особо. Например, для нормального закона, оба параметра которого оцениваются по выборке, для больших z > 0 (т.е. для z → ∞).
найти не удалось, есть лишь приближенные формулы для критических значений, основанные на асимптотических разложениях. Сравнение расчетов по этим формулам с упомянутыми ранее таблицами показало их хорошее согласие. Как уже говорилось, для каждого параметрического семейства критические значения надо рассчитывать особо. Например, для нормального закона, оба параметра которого оцениваются по выборке, для больших z > 0 (т.е. для z → ∞).
![]() (3.3)
(3.3)
Если же математическое ожидание известно и равно, скажем, а, то по выборке приходится оценивать только дисперсию. В этом случае для больших z > 0
![]() (3.4)
(3.4)
Эти приближенные формулы дают хорошие результаты для малых вероятностей и больших объемов выборок, то есть для вероятностей, начиная примерно с 0.20 (и меньше) и для объемов n, начиная примерно с 100 (и больше).
1.4 Критерии согласия χ2 Фишера для сложной гипотезы
Для проверки сложных гипотез может быть использована и соответствующая модификация критерия хи-квадрат Пирсона. Главные заслуги здесь принадлежат Р. Фишеру. Приведу одну из его теорем (сохраняя обозначения из теоремы К. Пирсона).
Теорема Фишера. Пусть n – число независимых повторений опыта, который может заканчиваться одним из r (r – произвольное натуральное число) элементарных исходов, скажем, А1, …, Аr. Пусть вероятности этих элементарных исходов известны с точностью до некоторого неопределенного, скажем, k-мерного параметра ![]() = (
= (![]() 1, …,
1, …, ![]() k). Тогда эти вероятности являются функциями от
k). Тогда эти вероятности являются функциями от ![]() : Р(Аі) = рі(
: Р(Аі) = рі(![]() ). Будем предполагать, что функции р1(
). Будем предполагать, что функции р1(![]() ), …, рr(
), …, рr(![]() ) заданы, дифференцируемы,
) заданы, дифференцируемы, ![]() для всякого
для всякого ![]() , а параметр
, а параметр ![]() изменяется в ограниченной области пространства. Тогда при n → ∞ статистика:
изменяется в ограниченной области пространства. Тогда при n → ∞ статистика:
 (4.1)
(4.1)
асимптотически распределена по закону χ2 с r – k – l степенями свободы.
Существует много вариантов этой теоремы. Например, такое же, как выше, предельное распределение имеет статистика
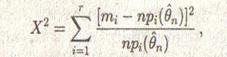 (4.2)
(4.2)
где ![]() n – оценка наибольшего правдоподобия для параметра
n – оценка наибольшего правдоподобия для параметра ![]() , найденная по частотам т1, …, тr. Поэтому значение (4.2) в дальнейшем можно использовать вместо (4.1). Далее, знаменатели прі в (4.1) и (4.2) можно заменить на ті, і = 1, …, r , и это не отразится на асимптотическом распределении χ2. Есть и другие возможности.
, найденная по частотам т1, …, тr. Поэтому значение (4.2) в дальнейшем можно использовать вместо (4.1). Далее, знаменатели прі в (4.1) и (4.2) можно заменить на ті, і = 1, …, r , и это не отразится на асимптотическом распределении χ2. Есть и другие возможности.
Статистика χ2 из (4.1) (и ее варианты) называется статистикой хи-квадрат Фишера для сложной гипотезы.
Статистику (4.1) (и ее варианты) можно использовать для проверки описанной выше сложной гипотезы о параметрическом виде вероятностей в схеме Бернулли
![]()
где р1(·), …, рr(·) – заданы, а параметр ![]() изменяется в заданной ограниченной области. Это можно делать так же, как мы делали с помощью статистики χ2 в случае простой гипотезы.
изменяется в заданной ограниченной области. Это можно делать так же, как мы делали с помощью статистики χ2 в случае простой гипотезы.
А именно, по наблюденным частотам т1, …, тr надо вычислить значение χ2 (4.1) либо (4.2) и затем сравнить его с критическими значениями распределения χ2 с числом степеней свободы (r – k – l), либо вычислить Р(χ2> χ2). Однако для использования аппроксимации хи-квадрат для распределения χ2 необходимо, чтобы число наблюдений было достаточно велико, и тем самым ожидаемые частоты прі(![]() ) не были малыми.
) не были малыми.
Как следует из формулировки теоремы, объект ее применения – испытания с конечным числом исходов. Чтобы использовать ее в условиях другого эксперимента – например, для проверки гипотезы о типе непрерывного или дискретного распределения с бесконечным (или конечным, но большим) числом исходов – этот эксперимент надо предварительно превратить в схему Бернулли. Раньше уже говорилось, как это делается обычно – путем разбиения выборочного пространства на непересекающиеся области. Параметрический (зависящий от параметра ![]() ) закон распределения вероятностей во всем пространстве, соответствие которого нашей выборке мы хотим проверить, превращается при этом в параметрическое распределение вероятностей между выбранными r областями.
) закон распределения вероятностей во всем пространстве, соответствие которого нашей выборке мы хотим проверить, превращается при этом в параметрическое распределение вероятностей между выбранными r областями.
Понятно, что результат последующего применения критерия хи-квадрат (принять гипотезу, отвергнуть гипотезу) сильно зависит от описанного перехода. К этому следует добавить условие применимости распределения χ2, которое требует, чтобы ожидаемые частоты были достаточно большими. (условие на ожидаемые частоты часто приходиться заменять требованием, чтобы не были малы наблюдаемые частоты т1, …, тr.) становится ясно, что подготовка к применению критерия хи-квадрат в несвойственных ему составляет деликатную и не всегда простую проблему. Возникает даже опасность невольной подгонки выбираемого разбиения к желательному результату. Поэтому, строго говоря, разбиение пространства на области должно идти вне зависимости от результатов случайного эксперимента, т.е. вне влияния подлежащей обработке выборки.
Как же после всех этих предостережений можно применить теорему Фишера к проверке гипотезы о типе выборки? Обсудим это на примере нормального распределения, параметры которого (а, σ2) неизвестны.
Итак, есть выборка х1, …, хп большого объема, проверить нормальность которой мы хотим с помощью (4.1) или (4.2) или их модификаций. Прежде всего мы должны разбить числовую прямую на r непересекающихся областей, а еще прежде – выбрать само число r. Сейчас существует убеждение (подкрепленное асимптотическими исследованиями), что против гладкой альтернативы лучше брать r небольшим – несколько единиц. Если же конкурируют с нормальным распределением все другие возможности, число r стоит взять таким большим, какое позволяет последующее использование аппроксимации хи-квадрат.
Допустим, что r уже выбрано, и можно переходить к разбиению пространства на области. При этом надо позаботится о том, чтобы ожидаемые частоты этих областей были достаточно велики для того, чтобы для χ2 действовала аппроксимация χ2. поскольку истинное распределение вероятностей неизвестно, приходится опираться на какую-либо его оценку. В данном примере – на оценку
![]()
истинной функции распределения
![]()
Чтобы не ломать бесплодно голову над вопросом, какими должны быть вероятности этих областей, а точнее в данном случае – их приближенные значения, возьмем их одинаковыми. Иными словами, в качестве границ интервалов используем решения уравнений
![]() ,
, ![]()
Замечу, что в качестве оценки функций распределения можно использовать и выборочную функцию распределения Fn(х), и другие возможности. В этом случае границами интервалов разбиения будут служить выборочные квантили (порядковые статистики).
После того, как мы определили интервалы разбиения числовой прямой, подсчитываем частоты т1, …, тr, по которым будем вычислять потом статистику χ2 (4.1) или (4.2) или какую- либо эквивалентную.
Следует подчеркнуть, что согласно теореме Фишера, для вычисления участвующих в этих формулах вероятностей рі(![]() ) следует использовать частоты т1, …, тr, и только их. Никакой другой информацией пользоваться нельзя! Нельзя, например, использовать
) следует использовать частоты т1, …, тr, и только их. Никакой другой информацией пользоваться нельзя! Нельзя, например, использовать ![]() составлены по всей выборке ,а должны быть – по частотам ті.
составлены по всей выборке ,а должны быть – по частотам ті.
Можно даже сказать, какие последствия повлечет за собой нарушение этого запрета. Статистика χ2 не будет (асимптотически) следовать распределению χ2 с r – l степенями свободы (как было бы при точно известных параметрах). Ее функция распределения пройдет несколько выше. В качестве иллюстрации на рис. 4.1 приведе6м графики функций распределения хи-квадрат с 8, 10, 18 и 20 степенями свободы. Графики, соответствующие первым двум распределениям, выделяют область в которой будет проходить график функции распределения χ2 при r = 11, если для вычисления рі(![]() ) использовались оценки
) использовались оценки ![]() . Последние два графика задают область нахождения функции распределения χ2 при r = 21.
. Последние два графика задают область нахождения функции распределения χ2 при r = 21.
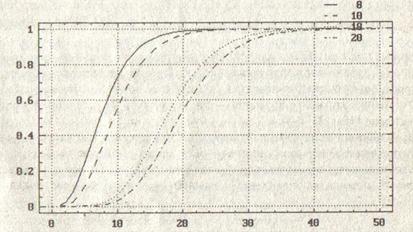
Рис. 4.1 функции распределения хи-квадрат с8,10,18 и 20 степенями свободы.
При больших r относительное развитие между квантилями распределений χ2 с (r – 3) и (r – 1) степенями свободы невелико. Поэтому последствия такой ошибки не опасны. Но при r следует действовать «по теории».
Из-за всех этих сложностей, условий и оговорок можно сделать вывод, что для проверки гипотезы о нормальности выборки критерий Р. Фишера подходит плохо. Правильнее вместо этого использовать модификации критериев Колмогорова или омега-квадрат. Но для многих распределений вероятностей (например – дискретных) другой возможности, чем обсуждаемый критерий хи-квадрат Фишера, просто нет.
Похожие работы
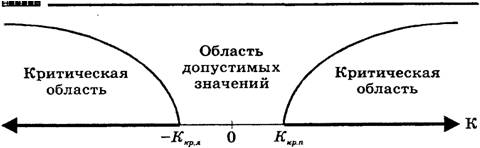
... ошибки первого рода; 3) определить область допустимых значений и так называемую критическую область; 4) принять то или иное решение на основе сравнения фактического и критического значений критерия. Проверка статистических гипотез складывается из следующих этапов: - формулируется в виде статистической гипотезы задача исследования; - выбирается статистическая характеристика гипотезы; - ...
... же для нахождения энергетически оптимальной концентрации эритроцитов в крови, парциального давления в артериальной и венозной крови, определения оптимальных функциональных параметров системы внешнего дыхания и др. 2 Принцип минимального воздействия в эколого-математических моделях Один из способов применения целевой функции состоит в формулировании общего утверждения относительно поведения ...
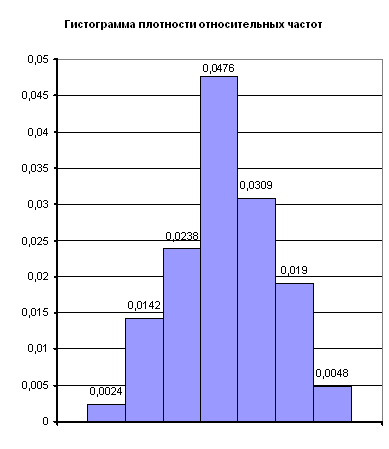
... в таблицу 4 Таблица 4 21.5 0.0025 28.5 0.0114 35.5 0.0291 42.5 0.0425 49.5 0.0351 56.5 0.0165 63.5 0.0044 3. Критерий согласия (Пирсона) Найду соответствующие вероятности для каждого разряда Из ТВ для нормальной случайной величины (8) Значения функции Лапласа, находим в приложении 2, учебника Вентцель Е.С., Овчаров Л.А., теория вероятностей и её ...
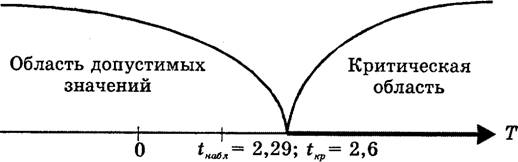
... Таблица 1 Среднее значение интервала, тыс. грн Фактическое количество предприятий 16 9 20 45 24 16 28 24 32 18 36 12 40 6 Всего 100 Тесты для закрепления материала Тест 1 В статистике критерий Стьюдента обозначается: а) критерий; б) ; в) критерий. Тест 2 Мощность критерия – это: а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является ...

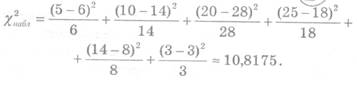
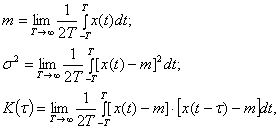
0 комментариев