Навигация
2. Точка на поверхні. Нехай
![]()
є рівняння поверхні, яка для спільності передбачається рухомою. Даючи змінному ![]() певне значення, ми бачимо, що
певне значення, ми бачимо, що ![]() повинні задовольняти умові
повинні задовольняти умові
![]()
що виражає, яке можливе переміщення допускається зв'язком існуючий в момент ![]() . Якщо виразити координати точки поверхні у функціях двох параметрів, то одержимо
. Якщо виразити координати точки поверхні у функціях двох параметрів, то одержимо
![]()
і співвідношення (1) повинне мати місце, які б не були ![]() і
і ![]() . Таким чином вийдуть рівняння руху.
. Таким чином вийдуть рівняння руху.
3. Точка на кривій. Нехай
![]()
- рівняння кривої. Величини ![]() повинні задовольняти дві умови
повинні задовольняти дві умови
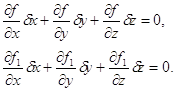
Допустимо, що координати точки кривої виражені у функції одного параметра:
![]()
Тоді найбільш загальне переміщення на кривій в положенні, яке вона займає у момент ![]() , вийде, якщо дати величині
, вийде, якщо дати величині ![]() приріст
приріст ![]() . Тому маємо:
. Тому маємо:
![]()
і рівняння (1), після скорочення на множник ![]() , прийме вигляд
, прийме вигляд

Розділ 2. Методика розв’язування задач
2. 1. Методика розв’язування задач за принципом можливих переміщень
При застосуванні принципу можливих переміщень до розв'язування конкретних задач можна рекомендувати додержувати такої послідовності дій:
1. Визначити систему матеріальних точок або тіл, рух яких необхідно розглянути.
2. Визначити число степенів вільності цієї системи.
3. Визначити характер в’язей, які накладені на дану матеріальну систему, тобто визначити, чи є ці в'язі ідеальними, чи ні. В останньому випадку, як було вказано вище, сили тертя слід віднести до заданих сил.
4. Якщо деякі з реакцій в'язей, які здебільшого виключаються з розгляду внаслідок їх ідеальності, необхідно визначній, то в цьому випадку, мислено відкидаючи в’язь, заміняють її реакцією і, переводячи реакцію в розряд заданих сил, застосовують принцип можливих переміщень. При цьому в’язі, реакції яких необхідно визначити, по черзі відкидають так, щоб у рівняння входила тільки одна невідома сила. Якщо необхідно визначити реакцію шарніра, то її розкладають по напрямах осей координат і після цього визначають спочатку одну складову, а потім іншу. Щоб визначити горизонтальну складову, шарнір слід замінити ротком на горизонтальній площині, а не відкидати в’язь повністю, бо реакція має ще й вертикальну складову, яка на можливому у цьому випадку горизонтальному переміщенні роботи не створює і, таким чином, буде виключена з відповідного рівняння. Після цього аналогічним способом визначають вертикальну складову, замінивши шарнір котком на вертикальній площині.
5. Скласти схему заданих сил, прикладених до точок матеріальної системи.
6. Надати системі одного з можливих переміщень. При виборі цього переміщення, якщо система має кілька степенів вільності, слід простежити за тим, щоб з рівняння не були виключені елементи, які необхідно визначити, і щоб рівняння мало найбільш простий вигляд.
7. Показати напрями переміщень окремих точок матеріальної системи, до яких прикладені задані сили.
8. Визначити роботу заданих сил на відповідних можливих переміщеннях і скласти рівняння на підставі принципу можливих переміщень. Очевидно, що таких рівнянь можна скласти стільки, скільки степенів вільності має дана матеріальна система.
9. Встановити залежність між можливими переміщеннями точок системи і визначити, таким чином, можливі переміщення всіх точок системи у функції від незалежних одне від одного можливих переміщень, виходячи з міркувань, вказаних вище.
В результаті цього виходить система рівнянь, кількість яких відповідає кількості степенів вільності матеріальної системи. Виключивши з цих рівнянь незалежні одне від одного можливі переміщення внаслідок їх довільності, можна визначити шукані сили або інші величини.
2. 2. Методика розв’язування задач за принципом Даламбера
При розв’язуванні задач за допомогою принципа Даламбера слід дотримуватись такої послідовності виконання дій:
1. Визначити систему матеріальних точок або тіл, рух яких необхідно розглянути.
2. Визначити число степенів вільності цієї системи.
3. Скласти схему заданих сил, прикладених до точок матеріальної системи.
4. Надати системі одного з можливих переміщень. При виборі цього переміщення, якщо система має кілька степенів вільності, слід простежити за тим, щоб з рівняння не були виключені елементи, які необхідно визначити, і щоб рівняння мало найбільш простий вигляд.
5. Показати напрями переміщень точок матеріальної системи, до яких прикладені задані сили.
6. Визначити роботу заданих сил на відповідних можливих переміщеннях і скласти рівняння на підставі принципу Даламбера.
7. Встановити залежність між можливими переміщеннями точок системи і визначити, таким чином, можливі переміщення всіх точок системи у функції від незалежних одне від одного можливих переміщень.
В кінцевому випадку виходить система рівнянь, після обробки яких можна визначити шукані величини.
Розділ 3. Приклади розв’язування задач
3. 1. Практичне застосування принципу можливих переміщень до розв’язування задач
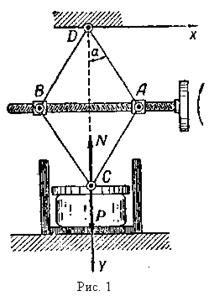 Задача 1. На маховичок колінчастого преса (рис. 1) діє пара сил з моментом М. Вісь маховичка має на кінцях гвинтову різь протилежних напрямів з відстанню Н і проходить через дві гайки, шарнірно прикріплені до двох вершин стержньового ромба з стороною а. Верхня вершина ромба закріплена нерухомо, нижня — прикріплена до горизонтальної плити преса. Визначити силу тиску преса Р на стискуваний кут при вершині ромба дорівнює 2х.
Задача 1. На маховичок колінчастого преса (рис. 1) діє пара сил з моментом М. Вісь маховичка має на кінцях гвинтову різь протилежних напрямів з відстанню Н і проходить через дві гайки, шарнірно прикріплені до двох вершин стержньового ромба з стороною а. Верхня вершина ромба закріплена нерухомо, нижня — прикріплена до горизонтальної плити преса. Визначити силу тиску преса Р на стискуваний кут при вершині ромба дорівнює 2х.
Позначимо через
![]()
швидкість поступального руху гайки, а через
![]()
кутову швидкість обертання маховичка. Тоді параметр гвинта визначається співвідношенням:
![]()
звідки
![]()
Якщо р=const, то ![]() . При повному оберті маховичка (
. При повному оберті маховичка (![]() ) поступальне переміщення гайки дорівнює s = h відстані гвинта. Тоді
) поступальне переміщення гайки дорівнює s = h відстані гвинта. Тоді ![]() .
.
Нехтуючи роботою сил тертя між гвинтом і гайками, а також між платформою і напрямними пазами, будемо вважати відповідні в'язі ідеальними. Щодо опори в точці D, то вона згідно з умовою задачі є нерухомою і її реакція роботи не виконує.
Реакцію N стискуваного предмета, яка за модулем дорівнює шуканому тискові преса Р, переведемо в розряд заданих сил. Таким чином, ми будемо розглядати рівновагу матеріальної системи (механізму преса), яка знаходиться під дією заданих сил і реакцій ідеальних в'язей - в даному випадку під дією обертального моменту М і сили N = -P.
Принцип можливих переміщень у цьому, випадку дає змогу записати:
![]() ,
,
де ![]() - можливе (вертикальне) переміщення горизонтальної плити преса, а
- можливе (вертикальне) переміщення горизонтальної плити преса, а ![]() - можливе обертальне переміщення маховичка.
- можливе обертальне переміщення маховичка.
Вибираючи координатну систему, як показано на рис. 1, знаходимо:
![]() .
.
Очевидно, що дана матеріальна система має один степінь вільності, що відповідає, наприклад, параметрові ![]() , який цілком визначає стан системи. Варіюючи функції
, який цілком визначає стан системи. Варіюючи функції ![]() і
і ![]() , дістанемо:
, дістанемо:
![]()
Тут ![]() є можливе переміщення гайки.
є можливе переміщення гайки.
Щоб знайти залежність ![]() від
від ![]() , скористаємося співвідношенням
, скористаємося співвідношенням ![]() , на підставі якого:
, на підставі якого:

(![]() і
і ![]() мають різні знаки, оскільки додатна робота моменту М викликає переміщення гайки у від’ємному напрямі осі Ох).
мають різні знаки, оскільки додатна робота моменту М викликає переміщення гайки у від’ємному напрямі осі Ох).
Підставимо тепер знайдені вирази для ![]() і
і ![]() у рівняння робіт:
у рівняння робіт:
![]()
або
![]()
Оскільки можливе переміщення ![]() довільне, то
довільне, то
![]()
звідки
![]()
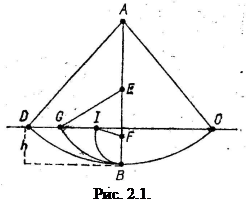
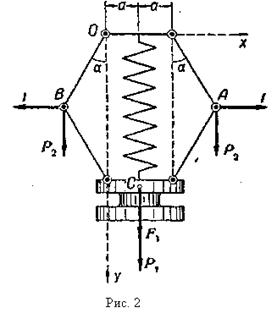 Задача 2. Відцентровий регулятор обертається з сталою кутовою швидкістю
Задача 2. Відцентровий регулятор обертається з сталою кутовою швидкістю ![]() 1/сек (рис. 2). Знайти залежність між кутовою швидкістю регулятора і кутом
1/сек (рис. 2). Знайти залежність між кутовою швидкістю регулятора і кутом ![]() відхилення його стержнів від вертикалі, якщо муфта ваги
відхилення його стержнів від вертикалі, якщо муфта ваги ![]() кг відтискається вниз пружиною з жорсткістю с кг/см, яка знаходиться при
кг відтискається вниз пружиною з жорсткістю с кг/см, яка знаходиться при ![]() у недеформованому стані і закріплена верхнім кінцем на осі регулятора. Вага куль дорівнює Р2 кг; довжина кожного стержня дорівнює l см; осі підвісу стержнів віддалені від осі регулятора на а см; вагою стержнів і пружини нехтуємо.
у недеформованому стані і закріплена верхнім кінцем на осі регулятора. Вага куль дорівнює Р2 кг; довжина кожного стержня дорівнює l см; осі підвісу стержнів віддалені від осі регулятора на а см; вагою стержнів і пружини нехтуємо.
Мислено видаляючи пружину, заміняючи її реакцію F і вважаючи решту в’язей ідеальними, розглянемо рух відцентрового регулятора під дією заданих сил: сил ваги ![]() куль А і В та сили ваги
куль А і В та сили ваги ![]() муфти, при цьому силу пружності пружини F також приєднуємо до числа заданих сил.
муфти, при цьому силу пружності пружини F також приєднуємо до числа заданих сил.
Вибравши координатну систему, як показано на рис. 2, впровадимо у розгляд відцентрові сили інерції I куль і складемо загальне рівняння механіки:
![]()
де ![]() - відповідні координати точок А і С;
- відповідні координати точок А і С; ![]() - можливі переміщення цих точок.
- можливі переміщення цих точок.
Легко бачити, що

Дана матеріальна система (регулятор) має при відсутності обертання навколо вертикальної осі (нами впроваджено відцентрові сили інерції I куль) один степінь вільності, який визначається кутом ![]() . Надаючи регуляторові можливого переміщення
. Надаючи регуляторові можливого переміщення ![]() , дістанемо для точок А і С можливі переміщення, варіюючи координати цих точок, виражені у функції від кута
, дістанемо для точок А і С можливі переміщення, варіюючи координати цих точок, виражені у функції від кута ![]() :
:

Сили інерції визначаються за формулою:
![]()
Сила пружності пружини дорівнює:
![]()
Рівняння робіт (загальне рівняння механіки) має вигляд:
![]()
Внаслідок довільності ![]() маємо:
маємо:
![]()
звідки
![]()
Задача 3. До шарніра В шарнірного чотиристоронника ![]() прикладена вертикальна сила R. Ланка ВС жорстко з’єднана з диском, центр якого знаходиться в точці В; до диска по дотичній прикладена горизонтальна сила
прикладена вертикальна сила R. Ланка ВС жорстко з’єднана з диском, центр якого знаходиться в точці В; до диска по дотичній прикладена горизонтальна сила ![]() (механізм для піднімання польового колеса плуга). Стержні мають довжину:
(механізм для піднімання польового колеса плуга). Стержні мають довжину: ![]() інші дані
інші дані ![]() показані на рис. 3. Нехтуючи вагою стержнів і диска, а також тертям у шарнірах, визначити співвідношення між величинами сил R і S у показаному на рисунку положенні рівноваги.
показані на рис. 3. Нехтуючи вагою стержнів і диска, а також тертям у шарнірах, визначити співвідношення між величинами сил R і S у показаному на рисунку положенні рівноваги.
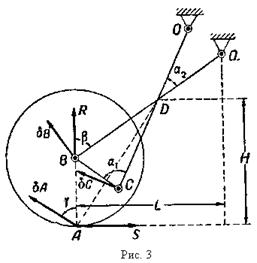 Розглядувана матеріальна система складається з диска, жорстко з'єднаного з стержнем ВС (цей диск з стержнем здійснюють плоский рух), і з двох стержнів СО і
Розглядувана матеріальна система складається з диска, жорстко з'єднаного з стержнем ВС (цей диск з стержнем здійснюють плоский рух), і з двох стержнів СО і ![]() . Нехтуючи тертям у шарнірних з'єднаннях ланок даного механізму і враховуючи нерухомість шарнірів О і
. Нехтуючи тертям у шарнірних з'єднаннях ланок даного механізму і враховуючи нерухомість шарнірів О і ![]() , будемо вважати в'язі ідеальними.
, будемо вважати в'язі ідеальними.
Оскільки швидкості точок В і С напрямлені нормально до стержнів ![]() і СО, то миттєвий центр швидкостей диска знаходиться в точці О. Тому можливі переміщення
і СО, то миттєвий центр швидкостей диска знаходиться в точці О. Тому можливі переміщення ![]() і
і ![]() точок В і А прикладання сил R і S мають напрями, відповідно нормальні до
точок В і А прикладання сил R і S мають напрями, відповідно нормальні до ![]() і
і ![]() . Вводячи для зручності кути
. Вводячи для зручності кути ![]() і
і ![]() , як показано на рис. 3, на підставі принципу можливих переміщень маємо:
, як показано на рис. 3, на підставі принципу можливих переміщень маємо:
![]()
звідки
![]()
Оскільки шарнірний чотирикутник ![]() має один стенінь вільності, то можливі переміщення
має один стенінь вільності, то можливі переміщення ![]() і
і ![]() залежать одне від одного. На підставі теореми про розподіл швидкостей маємо:
залежать одне від одного. На підставі теореми про розподіл швидкостей маємо:
![]()
Таким чином,
![]()
Враховуючи, що

остаточно дістанемо
![]()
3. 2. Практичне застосування принципу Даламбера до розв’язування задач
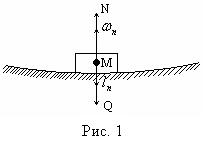 Задача 1. Радіус кривизни в найнижчій точці дугоподібного моста (рис. 1) дорівнює
Задача 1. Радіус кривизни в найнижчій точці дугоподібного моста (рис. 1) дорівнює ![]() . Найбільший нерухомий тягар, який може витримати середина моста дорівнює Р. Знайти, при якій швидкості v тягаря вагою I, що рухається по мосту, міст буде зруйновано. Припускаємо, що міст не деформується і що P>Q.
. Найбільший нерухомий тягар, який може витримати середина моста дорівнює Р. Знайти, при якій швидкості v тягаря вагою I, що рухається по мосту, міст буде зруйновано. Припускаємо, що міст не деформується і що P>Q.
Розглянемо положення рухомого тягаря М в момент проходження його через середину моста. На цей тягар діють сила ваги Q і реакція моста N. Для розв’язання задачі застосуємо принцип Даламбера. В цьому випадку сила інерції І має лише нормальну складову ![]() :
:
![]() .
.
На підставі принципу Даламбера
![]()
звідки
![]() .
.
Очевидно, міст не зруйнується, якщо ![]() , тобто при
, тобто при
![]()
або при
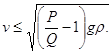
Таким чином, міст зруйнується при умові:
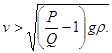
Відзначимо, що при вгнутому профілі моста тиск на міст з боку рухомого тягаря збільшується, а у випадку опуклого профілю - зменшується. Тому, враховуючи вимоги міцності споруди, вигідніше будувати мости з опуклим профілем.
Задача 2. Кулька О вагою Р = 0,5 кг, що лежить на горизонтальному столі, прив’язана ниткою завдовжки АО = І = 1 м до нерухомої точки А (рис.). Кульці надана початкова швидкість ![]() =2 м/сек, напрямлена в площині стола перпендикулярно до напряму нитки. Знайти швидкість кульки і натяг нитки через дві секунди після початку руху, якщо коефіцієнт тертя дорівнює k=0,1.
=2 м/сек, напрямлена в площині стола перпендикулярно до напряму нитки. Знайти швидкість кульки і натяг нитки через дві секунди після початку руху, якщо коефіцієнт тертя дорівнює k=0,1.
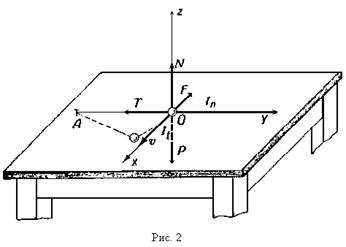
На кульку діють сила ваги Р і реакції нитки Т і стола N і F. Для розв'язання задачі застосуємо принцип Даламбера. Сила інерції I має дві складові - нормальну ![]() і тангенціальну
і тангенціальну ![]() :
:
![]() і
і ![]() .
.
Оскільки нормальне прискорення ![]() кульки напрямлене до точки А, то сила інерції
кульки напрямлене до точки А, то сила інерції ![]() напрямлена в протилежний бік. Сила тертя F має напрям, протилежний швидкості v, тому тангенціальне прискорення
напрямлена в протилежний бік. Сила тертя F має напрям, протилежний швидкості v, тому тангенціальне прискорення ![]() має напрям, протилежний напряму швидкості v. Отже, сила інерції
має напрям, протилежний напряму швидкості v. Отже, сила інерції ![]() , має напрям швидкості v.
, має напрям швидкості v.
На підставі принципу Даламбера
P+T+N+F+I=0,
або в проекціях на координатні осі:
![]()
звідки
![]()
Тангенціальне прискорення ![]() , протилежно напрямлене тангенціальній складовій
, протилежно напрямлене тангенціальній складовій ![]() сили інерції, тому
сили інерції, тому
![]()
або
![]()
звідки
![]()
Враховуючи початкові умови (при ![]() ), знайдемо
), знайдемо ![]() . Отже,
. Отже,
![]()
Таким чином, при t=2 сек., v=0,04 м/сек.. Натяг нитки в момент t=2 сек. дорівнює:
![]()
Задача 3. У кабіні підйомної машини під час піднімання зважують тіло М на пружинній вазі. Вага тіла дорівнює Р = 5 кг; натяг пружини (показання пружинної ваги) дорівнює Т=5,1 кг. Знайти прискорення кабіни.
На тіло М, розглядуване як матеріальна точка, Діють, сила ваги Р і реакція пружини Т (рис. 3). В зв'язку з тим, що за умовою задачі T>P, то рух точки М прискорений. Отже, прискорення ![]() напрямлене вгору. Відповідно до цього сила інерції
напрямлене вгору. Відповідно до цього сила інерції ![]() напрямлена вниз. Згідно з принципом Даламбера:
напрямлена вниз. Згідно з принципом Даламбера:

![]()
або
![]()
звідки
![]()
Коли б ми, не знаючи, як насправді напрямлене прискорення ![]() точки М, напрямили його вниз, а не вгору, тобто вважали б, що рух точки М сповільнений, то з рівняння рівноваги сил Р, Т і І дістали б для
точки М, напрямили його вниз, а не вгору, тобто вважали б, що рух точки М сповільнений, то з рівняння рівноваги сил Р, Т і І дістали б для ![]() від’ємне значення. Від’ємний знак при
від’ємне значення. Від’ємний знак при ![]() вказував би на те, що в дійсності рух не сповільнений, а прискорений.
вказував би на те, що в дійсності рух не сповільнений, а прискорений.
Висновок
Під час написання даної курсової роботи були розглянуті теоретичні засади принципу можливих переміщень та принципу Даламбера і перевірені на прикладах.
На підставі сказаного, для знаходження рівняння руху матеріальної точки за будь-яких умов досить виразити, що має місце рівновага між всіма силами, прикладеними до точки, і силою інерції. Це можна зробити методами аналітичної статики. Можна, наприклад, застосувати принцип можливих переміщень або принцип Даламбера. За допомогою цих принципів можна знаходити різні сили, які діють на тіло. Для цього потрібно розрізняти серед сил, прикладених до точки, сили задані і реакції зв'язків. При розв’язувані задач даними принципами, ми можемо використати отримані нами дані в практичних цілях, наприклад, при будівництві мостів, різних конструкцій тощо.
Список використаної літератури
1. Бать М. И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в примерах и задачах. – М.: Наука, 1991.
2. Жирнов Н. И. Классическая механика: Учебное пособие для студентов физико-математических факультетов педагогических институтов. – М.: Просвещение, 1980.
3. Путята Т. В., Фрадлін Б. Н. Методика розв’язування задач з теоретичної механіки. – К.: Радянська школа, 1955.
4. Сборник заданий для курсовых работ по теоретической механики, под ред. Яблонского. – М.: Высшая школа, 1985.
5. Турбин Б. Теоретическая механика. – М.: Сельхоз Гиз, 1959.
6. Блохинцев Д. И. Основы квантовой механики. – М.: Наука, 1976.
7. Давыдов А. С. Квантовая механика. – М.: ГИФМЛ, 1963.
8. Дирак П. Принципы квантовой механики. – М.: Наука, 1979.
9. Ландау Л. Д., Лифшиц Е. М. Квантовая механика: Курс теоретической физики. – М.: ГИФМЛ, 1963. – Т. III.
10. Левич В. Г., Вдовин Ю. А., Мямлин В. А. Курс теоретической физики. – М.: ГИФМЛ, 1962. – Т. II.
11. Месиа А. Квантовая механика. – М.: Наука, 1978. – Т. I, II.
12. Мякишев Г. Я. Динамические и статистические закономерности в физике. – М.: Наука, 1973.
13. Серова Ф. Г., Янкина А. А. Сборник задач по теоретической физике. – М.: Просвещение, 1979.
Похожие работы
... повинен увійти в шкільний курс фізики. Безперечно в курс потрібно включати ті питання історії, які в найбільшій мірі допомагають вирішенню завдань, які постають перед навчанням фізики. Звичайно, питання історії, що включаються в курс фізики, повинні бути тісно пов’язані з навчальною програмою і доступні школярам. Але ці положення не дають жорстких критеріїв для відбору історичних відомостей. Перш ...


0 комментариев