Метод Лагранжа

2.1 Метод Лагранжа

Описана вище процедура складає основу так називаного методу множників Лагранжа, що дозволяє ідентифікувати стаціонарні крапки при рішенні оптимізаційних задач з обмеженнями у виді рівностей. Схему цього методу можна формально представити в такий спосіб. Нехай

 L(x,)= (x, ) - g(x) .

Функція L називається функцією Лагранжа. Параметри  звуться множників Лагранжа і, як випливає з визначення, мають той же зміст, що і коефіцієнти чутливості описані вище. Рівняння

  і

виражають розглянуті вище необхідні умови наявності єкстремуми, що породжуються функцією Лагранжа безпосередньо. Це означає, що задача оптимізації з цільовою функцією f(x) при наявності обмеження g(х)=0 еквівалентна задачі перебування безумовного єкстремуми функції Лагранжа

 L(x, ). Достатні умови, використовувані при реалізації методу множників Лагранжа, формулюються нижче без доказу. Визначимо матрицю

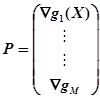 , де  і 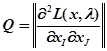 для всіх i і J

=+

Матриця Н^B являє собою так називану облямовану матрицю Гессе.

Нехай дана стаціонарна крапка (х₀, ₀₎ функції Лагранжа L (х, ), а облямована матриця Гессе Н^В сформована зі значень відповідних елементів у крапці (Хо, ₀). Тоді Х₀ є:

 1) крапкою максимуму, якщо, починаючи з головного мінору порядку (m+l), наступні (n-m) головних мінорів матриці Н^В утворять знакоперемінний числовий ряд, знак першого члена якого визначається множником ,(-1)^м+1;

 2) крапкою мінімуму, якщо, починаючи з головного мінору порядку (m+1), знак наступних (n-m) головних мінорів матриці Н^В визначається множником (-1)^м. Сформульовані умови виявляються достатніми для ідентифікації екстремальної крапки, але не є необхідними. Іншими Словами, стаціонарна крапка, що не задовольняє цим умовам, може бути екстремальною. Існують інші умови для ідентифікації екстремальних крапок, що є як необхідними, так і достатніми. Однак практичне використання цих умов у ряді випадків зв'язано зі значними обчислювальними труднощями. Визначимо матрицю

 утворену значеннями відповідних функцій у стаціонарній крапці (Хо, ₀). Тут µ - невідомий параметр, а Р и Q визначені вище. Нехай | |-визначник матриці ; тоді кожний з (n-m) дійсних коренів і i полінома | |=0 повинний бути:

 1)негативним, якщо хо - крапка максимуму;

 2)позитивним, якщо хо- крапка мінімуму.

Один з методів, що іноді застосовуються для рішення систем рівнянь, що виражають необхідні умови наявності екстремуми, полягає в послідовному виборі числових значень , після реалізації, якого дана система зважується відносно х.

3. ВИКОРИСТАННЯ МЕТОДУ ЯКОБІ ДЛЯ РІШЕННЯ ЗАДАЧ ЛІНІЙНОГО ПРОГРАМУВАННЯ

Дано задачу лінійного програмування, у якій потрібно максимізувати z=2xi+3xa

при обмеженнях х₁+х₂+х₃=5

 х_1-х2+х₄=3

 х₁,х₂,х₃,х₄>0

Розглянемо обмеження x_j>0 устанавлюючи не заперечність перемінних. Нехай W_J²- відповідна (ненегативна) додаткова перемінна. При цьому x- W_J² чи x=W_J² .Така заміна робить надлишковим умову не заперечності перемінних, і вихідна задача приймає наступний вид:

максимізувати z=2W₁²+3W₂²

 при обмеженнях W₁²+W₂²+W₃²=5,

W₁²-W₂²+W₄²=3.

 Щоб застосувати метод Якобі, покладемо

Y=(W₁,W₂) і Z=(W₃,W₄).

(Помітимо, що вектори Y і Z, якщо використовувати термінологію лінійного програмування, утворені базисними і небазисними перемінними відповідно). Маємо

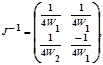  W₁ і W₂ 

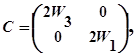
Рішення рівняння  з обмеженнями дозволяє визначити стаціонарну крапку (w₁=2, w₂=1, w₃= 0, w₄= 0) . При цьому матриця Гессе має вид

 Тому що Н_c- невизначена матриця, те стаціонарна крапка не є крапкою максимуму. Справді отриманий результат не є несподіваним, оскільки з теорії лінійного програмування випливає, що (небазисні) перемінні w₃ і w₄ (і, отже, х₃ і х₄ ) дорівнюють нулю. Це означає, що в залежності від конкретного вибору Y і Z рішення, отримане за допомогою методу Якобі, визначає відповідну екстремальну крапку багатогранника припустимих рішень. При цьому рішення може не бути оптимальним. Однак метод Якобі дозволяє ідентифікувати крапку оптимуму шляхом використання достатніх умов.

Відповідна стаціонарна крапка визначається набором значень W₁=0,

W₂ =5, W₃ =0 ,W₄ =8.

 Матриця

 є негативно визначеною. Таким чином, цьому рішенню відповідає крапка максимуму.

 Отриманий результат можна перевірити графічно, користаючись, мал.2. Перше рішення (х₁=4, х₂=1) не є оптимальним на відміну від другого (х₁=0, х₂=5), що виявляється оптимальним, читачу надається можливість перевірити, що дві екстремальні крапки багатогранника, що залишилися, припустимих рішень не є крапками максимуму. Крім того, використовуючи достатні умови, можна показати, що в екстремальній крапці (х₁=0, х₂=0) має місце мінімум.

 Слід зазначити, що у випадку рішення задачі лілейного програмування, уведені раніше, коефіцієнти чутливості  відіграють роль перемінних двоїстий задачі. Проілюструємо цей факт на розглянутому чисельному прикладі. Нехай u₁ і u_g - відповідні перемінні двоїстої задачі, значення яких у крапці оптимуму

(W₁=0, W₂ =5, W₃ =0 ,W₄ =8.) обчислюються по формулі:

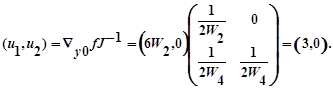
Відповідне значення цільової функції двоїстої задачі дорівнює 5u₁+3u₂= 15 і збігається з оптимальним значенням цільової функції прямої задачі. Отримане рішення також задовольняє обмеженням двоїстої задачі, і , отже, є оптимальним. Це означає, що коефіцієнти чутливості збігаються з перемінними двоїстої задачі. Справді, неважко помітити, що і ті й інші допускають однакову інтерпретацію.

 Тепер можна зробити трохи загальних висновків зі схеми застосування методу Якобі і рішенню задач лінійного програмування. Розглянутий чисельний приклад показує, що необхідні умови обчислення єкстремуми приводять до рівності нулю незалежних перемінних. Достатні умови вказують на діагональність матриці Гессе.

 Таким чином, усі діагональні елементи цієї матриці повинні бути позитивними у випадку наявності мінімуму і негативними у випадку наявності максимуму. З вищевикладеного випливає, що необхідна умова наявності екстремума еквівалентно твердженню про те, що для перебування оптимального рішення потрібно перевірити тільки "базисні" (припустимі) рішення. У цьому випадку незалежні перемінні відіграють роль небазисних перемінні задачі лінійного програмування. Достатня умова приводить до висновку про можливу наявність точної відповідності між діагональними елементами матриці Гессе і двоїстими оцінками Z_J-C_J, одержуваними за допомогою симплекса-методу. Отримане рішення також задовольняє обмеженням двоїстої задачі. Справді, неважко помітити, що і ті й інші допускають однакові інтерпретації. Це означає, що коефіцієнти чутливості збігаються з перемінними двоїстої задачі.

Похожие работы

Основи стандартизації та сертифікації

Скачать

349442

3

2

... побудови і функціонування системи сертифікації, її структура, функції та порядок виконання цих функцій регламентовані нормативними документами міжнародних організацій із стандартизації і сертифікації, насамперед документами І50, ІЕС, НАС, Європейської співдружності, а також ДСТУ. До правових аспектів сертифікації належать питання поширення відповідальності за спостереженням правил процедури ...