Навигация
Найдем состояния равновесия системы (2.8). Для этого приравняем правые части системы нулю
1. Найдем состояния равновесия системы (2.8). Для этого приравняем правые части системы нулю

Рассмотрим два случая:

Получаем:
![]()
![]()

Из первого уравнения найдем y:
![]()
и подставляя y во второе уравнение получим:
![]()
Решая это уравнение, находим:
![]() .
.
Итак, получаем
![]() ,
, ![]()
![]() ,
, ![]()
Итак, получаем точки
![]() ,
, ![]() ,
, ![]() ,
, ![]()
и прямую x=0, которая является траекторией системы (2.8).
2. Исследуем поведение траекторий в окрестностях состояний равновесия ![]()
Исследуем точку ![]() .
.
Составим характеристическое уравнение в точке ![]() .
.

Отсюда
![]()
![]() (2.11)
(2.11)
![]()
![]()
Следовательно, характеристическое уравнение примет вид:

Характеристическими числами для точки ![]() системы (2.8) будут
системы (2.8) будут
![]() ,
, ![]() .
.
Корни ![]() - действительные и различных знаков не зависимо от параметра d, значит точка
- действительные и различных знаков не зависимо от параметра d, значит точка ![]() - седло.
- седло.
Исследуем точку ![]() .
.
Согласно (2.11) составим характеристическое уравнение в точке ![]() :
:
![]()
Характеристическими числами для точки ![]() системы (2.8) будут
системы (2.8) будут
![]() ,
, ![]() .
.
Корни ![]() - действительные и одного знака, зависящие от параметра d. Если d<0, то точка
- действительные и одного знака, зависящие от параметра d. Если d<0, то точка ![]() - неустойчивый узел, а если d>0, то точка
- неустойчивый узел, а если d>0, то точка ![]() - устойчивый узел.
- устойчивый узел.
3. Исследуем поведение траекторий в окрестности точки ![]() .
.
Составим характеристическое уравнение согласно (2.11)
 .
.
Характеристическими числами для точки ![]() системы (2.8) будут
системы (2.8) будут
![]() ,
, ![]()
Корни ![]() - действительные и одного знака, зависящие от параметра d. Если d<0, то точка
- действительные и одного знака, зависящие от параметра d. Если d<0, то точка![]() - устойчивый узел, если d>0, то точка
- устойчивый узел, если d>0, то точка ![]() - неустойчивый узел.
- неустойчивый узел.
4. Исследуем поведение траекторий в окрестности точки ![]() .
.
Согласно (2.11) составим характеристическое уравнение:
![]()
![]()
Характеристическими числами для точки ![]() системы (2.8) будут
системы (2.8) будут
![]() ,
, ![]()
Корни ![]() - действительные и разных знаков не зависимо от параметра d, следовательно
- действительные и разных знаков не зависимо от параметра d, следовательно ![]() - седло.
- седло.
Исследуем бесконечно - удаленную часть плоскости системы (2.8) вне концов оси oy. Преобразование [7] ![]() переводит систему (2.8) в систему:
переводит систему (2.8) в систему:
 (2.12)
(2.12)
где ![]() .
.
Изучим бесконечно - удаленные точки на оси U, то есть при z=0. Получаем:
![]()
![]()
Следовательно ![]() .
.
Таким образом, получаем две точки N1 (0,-1) и N2 (0,1), которые являются состоянием равновесия. Исследуем характер этих точек обычным способом.
Составим характеристическое уравнение в точке N1 (0,-1).
![]()
![]()
![]() (2.13)
(2.13)
![]()
Имеем:
![]()
![]() ,
, ![]() .
.
Корни ![]() -действительные и различные по знаку, следовательно точка N1 (0,-1) - седло.
-действительные и различные по знаку, следовательно точка N1 (0,-1) - седло.
Исследуем точку N2 (0,1).
Согласно (2.13) составим характеристическое уравнение:
![]()
![]() ,
, ![]() .
.
Корни ![]() -действительные и одного знака, значит точка N2 (0,1) - устойчивый узел.
-действительные и одного знака, значит точка N2 (0,1) - устойчивый узел.
Исследуем концы оси y с помощью преобразования [7] ![]() . Это преобразование переводит систему (2.8) в систему:
. Это преобразование переводит систему (2.8) в систему:
 (2.14)
(2.14)
где ![]() .
.
Для исследования состояний равновесия на концах оси y, нам необходимо исследовать только точку N3 (0,0). Составим характеристическое уравнение в точке N3 (0,0):
![]()
![]()
Корни ![]() - действительные и одного знака, значит точка N3 (0,0) - неустойчивый узел.
- действительные и одного знака, значит точка N3 (0,0) - неустойчивый узел.
Теперь дадим распределение состояний равновесия системы (2.1) в виде таблицы 2.
Таблица 2.
| d |
|
|
|
| ∞ | ||
| N1 | N2 | N3 | |||||
| (-∞; 0) | седло | неуст. узел | уст. узел | седло | седло | уст. узел | неуст. узел |
| (0; +∞) | седло | уст. узел | неуст. узел | седло | седло | уст. узел | неуст. узел |
Положение кривых (2.9), (2.10) и расположение относительно их состояний равновесия при d<0 и d>0 дается соответственно рис.2 (а, б).
Поведение траекторий системы в целом при d<0 и d>0 дается рис.5 (а, б) приложения Б: Поведение траекторий системы (2.8).
Вопрос о существовании предельных циклов не возникает, так как Воробьев А.П. [5] доказал, для квадратичной системы предельный цикл не может окружать узел.
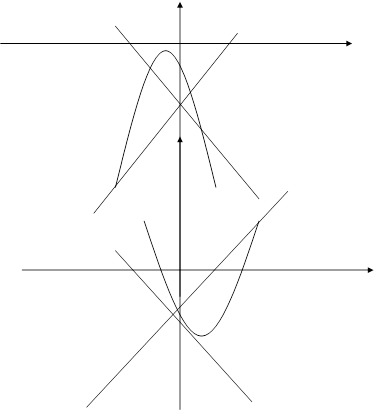
а (d<0) б (d>0)
Рис. 2
2.3 Исследование системы (1.1) с коэффициентами, заданными формулами (1.52) - (1.53)
Будем проводить наше исследование в предположении, что
![]() ,
, ![]()
![]()
![]() .
.
Пусть мы имеем систему (1.1), коэффициенты которой определяются формулами (1.52) - (1.53). Тогда система (1.1) будет иметь вид:
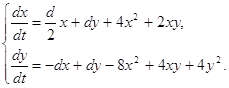 (2.15)
(2.15)
Интегральные кривые в этом случае имеют вид:
![]() (2.16)
(2.16)
![]() (2.17)
(2.17)
То есть частные интегралы (1.3) и (1.13) преобразовываются в прямые таким образом, что интегральная кривая (2.16) совпадает с одной из прямых интегральной кривой (2.17).
Найдем состояния равновесия системы (2.15). Приравняв правые части системы нулю, и исключив переменную y, получим следующее уравнение для определения абсцисс состояний равновесия:
![]() (2.18)
(2.18)
Из (2.18) получаем, что
![]() ,
, ![]() ,
, ![]() .
.
Ординаты точек покоя имеют вид:
![]() ,
, ![]() ,
, ![]() .
.
Итак, имеем точки
![]() ,
, ![]() ,
, ![]() .
.
Исследуем поведения траекторий в окрестностях состояний равновесия ![]() .
.
Исследуем состояние равновесия в точке ![]() .
.
Составим характеристическое уравнение.

Отсюда
![]()
![]() (2.19)
(2.19)
![]()
![]()
Следовательно, характеристическое уравнение примет вид

Имеем
![]() ,
,
Или
![]() .
.
Характеристическими числами для точки ![]() для системы (2.15) будут
для системы (2.15) будут
![]() .
.
Корни ![]() - комплексные и зависят от параметра d. Значит, если d<0, то точка
- комплексные и зависят от параметра d. Значит, если d<0, то точка ![]() - устойчивый фокус, если d>0, то точка
- устойчивый фокус, если d>0, то точка ![]() - неустойчивый фокус.
- неустойчивый фокус.
Исследуем точку
![]() .
.
Согласно (2.19) составим характеристическое уравнение в точке
![]() .
.
Имеем
 .
.
![]()
Характеристическими числами для точки ![]() системы (2.15) будут
системы (2.15) будут
![]() ,
, ![]()
Корни ![]() - действительные и различных знаков не зависимо от параметра d. Следовательно, точка
- действительные и различных знаков не зависимо от параметра d. Следовательно, точка ![]() - седло.
- седло.
3. Исследуем точку ![]() .
.
По (2.19) составим характеристическое уравнение в точке ![]() .
.
Получим

![]() .
.
Решая уравнение, получим
![]() ,
,
то есть
![]() ,
, ![]()
Корни ![]() - действительные и одного знака, зависящие от параметра d. Если d<o, то точка
- действительные и одного знака, зависящие от параметра d. Если d<o, то точка![]() - неустойчивый узел, если d>0, то точка
- неустойчивый узел, если d>0, то точка ![]() - устойчивый узел.
- устойчивый узел.
Исследуем бесконечно - удаленную часть плоскости вне концов оси oy преобразованием [7] ![]() Это преобразование систему (2.15) переводит в систему:
Это преобразование систему (2.15) переводит в систему:
 (2.20)
(2.20)
где ![]() .
.
Изучим бесконечно - удаленные точки на оси u, то есть при z=0. Получаем
![]()
![]()
![]()
Следовательно ![]()
Итак, имеем две точки N1 (0,2) и N2 (0,-2).
Исследуем характер этих точек обычным способом. Составим характеристическое уравнение в точке N1 (0,2).
![]()
![]()
![]() (2.21)
(2.21)
![]() .
.
Следовательно
![]()
![]() ,
, ![]()
Воспользуемся параллельным переносом
![]()
![]()
и подставим z, u в систему (2.20). Получим новую систему:
 (2.22)
(2.22)
Составим характеристическое уравнение в точке N2 (0,-2)
![]()
Характеристическими числами для точки N2 (0,-2), будут
![]() ,
, ![]() -
-
сложное состояние равновесия.
Для определения характера состояния равновесия воспользуемся теоремой [2, с. 196-198].
Теорема 2.1. Пусть точка (0,0) - изолированное состояние равновесия системы:
 (2.23)
(2.23)
где ![]() ,
,![]() есть полиномы от x,y начиная со второй степени,
есть полиномы от x,y начиная со второй степени, ![]() - решение уравнения
- решение уравнения ![]() , а разложение функции
, а разложение функции ![]() имеет вид:
имеет вид:
![]()
Тогда
1) при m - нечетном и ![]() m>0 точка (0,0) - есть топологический узел;
m>0 точка (0,0) - есть топологический узел;
при m - нечетном и ![]() m<0 точка (0,0) - есть топологическое седло;
m<0 точка (0,0) - есть топологическое седло;
при m - четном точка (0,0) есть седло - узел, то есть такое состояние равновесия, каноническая окрестность которого состоит из параболистического и двух гиперболических секторов. При этом
если ![]() m<0, то внутри гиперболических секторов заключен отрезок положительной полуоси OX, примыкающий к точке (0,0);
m<0, то внутри гиперболических секторов заключен отрезок положительной полуоси OX, примыкающий к точке (0,0);
если ![]() m>0, то отрезок отрицательной полуоси OX.
m>0, то отрезок отрицательной полуоси OX.
Чтобы воспользоваться теоремой, необходимо систему (2.22) привести к виду:

Это можно сделать, воспользовавшись одним из следующих преобразований [2, с. 199-201]:
если ![]() ,
, 
если ![]() ,
, ![]() ,
, 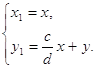
если ![]() ,
, ![]() ,
, 
где a, b, c, d - коэффициенты системы (2.23).
Тогда для системы (2.22) возьмем следующее преобразование:
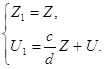
Получим
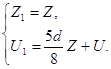

Тогда
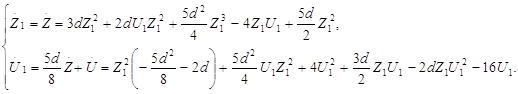 (2.24)
(2.24)
Найдем решение уравнения:
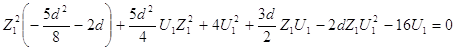
в виде ряда по степеням Z1:
![]()
![]()
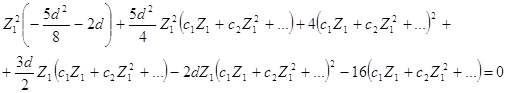
![]()
![]()
![]()
![]()
Следовательно
![]()
Тогда
![]()
Подставляя U1 в систему (2.24) получим:

Отсюда
![]() ,
, ![]() >0.
>0.
Следовательно, по теореме 2.1 получаем, что точка N2 (0,-2) - седло - узел.
Исследуем концы оси y с помощью преобразования [7] ![]() . Это преобразование переводит систему (2.15) в систему:
. Это преобразование переводит систему (2.15) в систему:
 (2.25)
(2.25)
где ![]() .
.
Для исследования состояний равновесий на концах оси y, нам необходимо исследовать только точку N3 (0,0). Составим характеристическое уравнение в точке N3 (0,0)
![]()
Соответственно характеристическими числами будут
![]()
Корни ![]() - действительные и одного знака. Следовательно, точка N3 (0,0) - устойчивый узел.
- действительные и одного знака. Следовательно, точка N3 (0,0) - устойчивый узел.
Теперь дадим распределение состояний равновесия системы (2.1) в виде таблицы 3.
Таблица 3.
| d |
|
|
| ∞ | ||
| N1 | N2 | N3 | ||||
| (-∞; 0) | уст. фокус | седло | неуст. узел | седло | седло-узел | уст. узел |
| (0; +∞) | неуст. фокус | седло | уст. узел | седло | седло-узел | уст. узел |
Положение кривых (2.16), (2.17) и расположение относительно их состояний равновесия при d<0 и d>0 дается соответственно рис.3 (а, б).
Поведение траекторий системы в целом при d<0 и d>0 дается Рис.6 (а, б) приложения В: Поведение траекторий системы (2.15).
Вопрос существования предельных циклов остается открытым.

а (d<0)

б (d>0)
Рис. 3
Заключение
В данной дипломной работе построена квадратичная двумерная стационарная система при условии, что частным интегралом является кривая четвертого порядка, которая распадается на две кривые второго порядка, одна из которых парабола, вторая окружность или гипербола. При этом коэффициенты кривых выражаются через произвольный параметр системы.
Проведено качественное исследование системы. Найдены необходимые и достаточные условия существования у системы двух частных интегралов. В зависимости от коэффициентов были рассмотрены 3 случая. Найдены состояния равновесия трех полученных систем, которые принадлежат интегральным кривым. Исследована бесконечно-удаленная часть плоскости систем, в двух из которых доказано отсутствие предельных циклов. Выяснено поведение сепаратрис седел и построена качественная картина поведения траекторий систем в круге Пуанкаре.
Список использованных источников
1. Баутин Н.Н. О числе предельных циклов, появляющихся при изменении коэффициентов из состояния равновесия типа фокуса или центра // Матем. сб. - 1952. - Т.30,№1. - 458 с.
2. Баутин Н.Н., Леонтович Е.А. Методы и приемы качественного исследования динамических систем на плоскости. - М.: Наука, 1976. - 274 с.
3. Бендиксон И. О кривых, определяемых дифференциальными уравнениями. - УМН, 1941. - Вып.9. - 643 с.
4. Биркгоф Дж.Д. Динамические системы. М. - Л.: Гостехиздат, 1941. - 340 с.
5. Воробьев А.П. К вопросу о циклах вокруг особой точки типа “узел" // ДАН БССР. - 1960. - Т.4,№9. - 720 с.
6. Еругин Н.П. Построение всего множества систем дифференциальных уравнений, имеющих заданную интегральную кривую. - ПММ. - 1952. - Т.16, Вып.6. - с.659-670.
7. Пуанкаре А. О кривых, определяемых дифференциальными уравнениями. - М. - Л.: ГИТТЛ, 1947. - 839 с.
8. Серебрякова Н.Н. Качественное исследование одной системы дифференциальных уравнений теории колебаний. - ПММ. - 1963 Т.27, Вып.1. - 230 с.
9. Филипцов В.Ф. К вопросу алгебраических интегралов одной системы дифференциальных уравнений // Дифференц. уравнения. - 1973. - Т.9,№3. - 256 с.
10. Черкас Л.А. Об алгебраических решениях уравнения ![]() , где P и Q - многочлены второй степени // ДАН БССР. - 1963. - Т.7,№11. - 950 с.
, где P и Q - многочлены второй степени // ДАН БССР. - 1963. - Т.7,№11. - 950 с.
11. Яблонский А.И. Алгебраические интегралы одной системы дифференциальных уравнений // Дифференц. уравнения. - 1970. - Т.6,№10. - с.1752-1760.
Приложение А
Поведение траекторий системы (2.1)

а) (d<0)
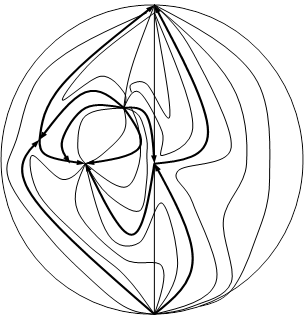
б) (d>0)
Рис. 4
Приложение Б
Поведение траекторий системы (2.8)

а) (d<0)

б) (d>0)
Рис. 5
Приложение В
Поведение траекторий системы (2.15)

а) (d<0)
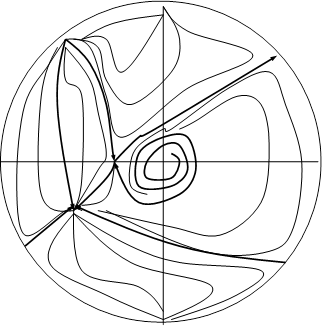
б) (d>0)
Рис. 6
Похожие работы
... в целом выделенных в первом разделе классов систем при фиксированных значениях некоторых параметров. 1. Построение квадратичной двумерной стационарной системы 1.1 Построение квадратичной двумерной стационарной системы с частным интегралом в виде кривой второго порядка Рассмотрим систему дифференциальных уравнений: В данной работе будем рассматривать систему, в случае когда ...
... (0.5) в предположении, что коэффициенты кривых (0.4), (0.5) и системы (0.3) вещественные. Работа состоит из двух глав. В первой главе проводится построение квадратичной двумерной стационарной системы с частными интегралами в виде кривых третьего и первого порядков. При этом коэффициенты интегралов выражаются через коэффициенты системы, а коэффициенты системы связаны между собой тремя ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
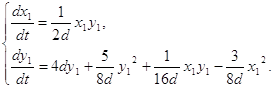
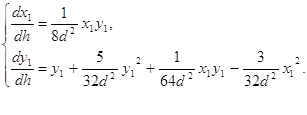
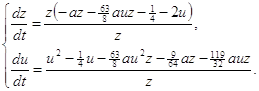
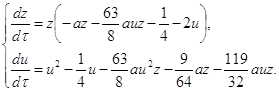
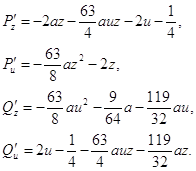
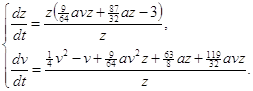
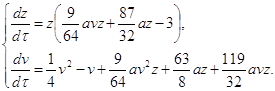




0 комментариев