Навигация
Построение квадратичной двумерной стационарной системы с частным интегралом в виде кривой первого порядка
1.2 Построение квадратичной двумерной стационарной системы с частным интегралом в виде кривой первого порядка
Пусть система (1) наряду с интегралом (1.3) имеет интеграл вида:
mx+ny+p=0. (1.11)
Будем рассматривать теперь систему:
![]()
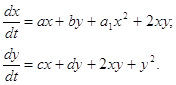 (1.12)
(1.12)
Согласно формуле (1.4), где L (x, y)=Mx+Ny+P, M, N, P-постоянные, получаем равенство:
m (ax+by+a1x2+2xy)+n (cx+dy+2xy+y2)=(mx+ny+p) (Mx+Ny+P).
Приравнивая коэффициенты при одинаковых степенях xmyn слева и справа, получим равенства:
(a1–M) m=0
(2-N) m+(2-M) n=0 (1.13)
(N-1) n=0
(a–P) m+cn–Mp=0
bm+(d–P) n–Np=0 (1.14)
Pp=0
Предполагаем, что кривая не проходит через начало координат, тогда p≠0, значит Р=0.
Из равенств (1.13) получаем, что М=а1, N=1,
n=![]() m, (1.15)
m, (1.15)
p= (![]() ) m, m≠0.
) m, m≠0.
Подставим эти коэффициенты в уравнение (1.14) и получим ещё одно условие на коэффициенты системы, которое совпадает с условием (1.8), то есть:
(a1–2) a–a1(a1–2) b+c–a1d =0.
Итак, имеет место следующая теорема:
Теорема 1.2 Система

Имеет частный интеграл mx+ny+p=0, коэффициенты которого выражаются формулами
n=![]() m, p= (
m, p= (![]() ) m, m≠0,
) m, m≠0,
При условии, что коэффициенты системы связаны соотношением:
(a1–2) a–a1(a1–2) b+c–a1d =0 и а1≠0, а1≠2.
1.3 Необходимые и достаточные условия существования у двумерной стационарной системы двух частных интегралов в виде кривых первого и второго порядков
В подразделах 1.1–1.2 мы получили что система (1.1) будет иметь два частных интеграла в виде кривой первого порядка и кривой второго порядка, при условии, что коэффициенты системы связаны соотношениями:
(a1–2) a–a1(a1–2) b+c–a1d =0, (1.16)
2 ((a1–2) a – a1 (a1–2) b–a1d+c) ((a1–2) a+a1d)=0.
Причём а1≠0, а1≠2, в1=в2=с2=1.
1. Рассмотрим случай (a1–2) a–a1(a1–2) b+c–a1d =0, (a1–2) a+a1d=0.
Из этих равенств получили:
а= -![]() d, d≠0
d, d≠0
c=a1(a1–2) b+2a1d.
Так как коэффициент d можно взять любым, неравным нулю, тогда предположим, что b=2d. Из следующих предположений, получаем:
b=2d,
a= -![]() d, (1.17)
d, (1.17)
c=2a1(a1–1) d, d≠0, а1≠2.
Получили, что коэффициенты системы (1.1) определяются формулами (1.17), при условиях (1.16), в которых параметры b1=b2=с2=1, а1≠0.
Выражения (1.6), (1.9), (1.15) при условии, что имеют место (1.17), дадут следующие выражения для коэффициентов интегралов (1.3) и (1.11):
α=2 (a1–2),
β=(a1–2)2,
γ=2 (2а1–3) d,
δ=2 (а1–2) (2а1–3) d, (1.18)
σ=(2а1–1) d2,
n=![]() m,
m,
p=![]() md, m≠0, d≠0, a1≠2, a1≠0.
md, m≠0, d≠0, a1≠2, a1≠0.
Имеет место следующая теорема:
Теорема 1.3 Система
![]()
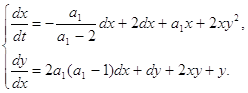
Имеет частные интегралы вида:
y2+2 (a1–2) xy+(a1–2)2x2+2 (2a1–3) d+
+2 (a1–2) (2a1–3) dx+(2a1–1) d2=0
и (a1–2) x+y+(2a1–3) d=0,
При условии, что коэффициенты системы (1.1) выражаются через параметры а1 и d по формулам (1.17) и в1=в2=с2=1.
2. Рассмотрим случай:
(a1–2) a–a1(a1–2) b+c–a1d =0.
Выразим из этого условия коэффициент с, получим
с= a1(a1–2) b+ a1d – (a1–2) a.
Воспользуемся предположением из первого случая, что в=2d, d≠0, тогда коэффициент с=а1(2а1–3) d – (а1–2) а.
Так как d-любое число, неравное нулю, предположим, что а=2а1d.
Из соотношения (a1–2) a–a1(a1–2) b+c–a1d =0, при условиях, что b=2d, a=2a1d, d-любое число, d≠0, получим формулы, выражающие коэффициенты системы (1.1) через параметр а1 и коэффициент d, то есть: a=2a1d,
b=2d, (1.19)
c=a1d.
Равенства (1.6) – (1.9) и (1.14) при условии, что имеют место формулы (1.19), дадут следующие выражения для коэффициентов интегралов (1.3) и (1.11):
α=2 (a1–2),
β=(a1–2)2,
γ=2 (а1–1) d,
δ=2 (a1–![]() ) (a1–2) d, (1.20)
) (a1–2) d, (1.20)
σ=(a1–![]() )2d2,
)2d2,
n=![]() m,
m,
p=m![]() d, a1≠2, d≠0, m≠0.
d, a1≠2, d≠0, m≠0.
Теорема 1.4 Система
![]()
![]() 2a1dx+2dy+a1x2+2xy,
2a1dx+2dy+a1x2+2xy,
![]() =a1dx+dy+2xy+y2
=a1dx+dy+2xy+y2
Имеет частные интегралы вида:
y2+2 (a1–2) xy+(a1–2)2x2+2 (a1–1) dy+2 (a1–![]() ) (a1–2) dx+(a1–
) (a1–2) dx+(a1–![]() )2d2=0
)2d2=0
и
(a1–2) x+y+(2a1–3) d=0,
При условиях, что коэффициенты системы (1.1) выражаются через параметры а1 и d по формулам (1.19) и в1=в2 =с2=1, а1≠2, а1≠0, d-любое число.
Похожие работы
... (0.5) в предположении, что коэффициенты кривых (0.4), (0.5) и системы (0.3) вещественные. Работа состоит из двух глав. В первой главе проводится построение квадратичной двумерной стационарной системы с частными интегралами в виде кривых третьего и первого порядков. При этом коэффициенты интегралов выражаются через коэффициенты системы, а коэффициенты системы связаны между собой тремя ...
... третьего порядка. Яблонский А.И. [11, с.1752 - 1760] и Филипцов В.Ф. [9, с.469-476] изучали квадратичные системы с предположением, что частным интегралом являлись алгебраические кривые четвертого порядка. В данной работе рассматривается система (0.3) и проводится качественное исследование в целом системы (0.3) при условии, что частным интегралом является кривая четвертого порядка, которая ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
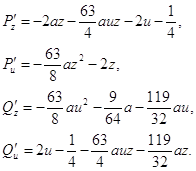
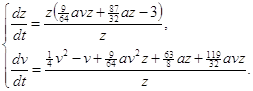
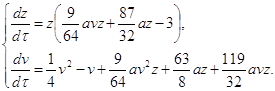
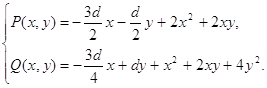
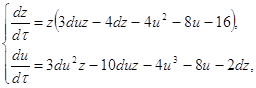





0 комментариев