Навигация
Дведення координатним методом теореми про три перпендикуляри
4. Дведення координатним методом теореми про три перпендикуляри.
Теорема про три перпендикуляри: якщо пряма, проведена на площині через основу нахилої, перпендикулярна її проекції, то вона перпендикулярна нахилій. І навпаки: якщо пряма на площині перпендикулярна наклонній, то вона перпендикулярна і проекції нахилій.
Доведення. Нехай АВ- перпендикуляр до площини ![]() , АС –нахила та с- пряма в площині
, АС –нахила та с- пряма в площині ![]() , що проходить через основу С нахилої (малюнок 3). Проведемо пряму
, що проходить через основу С нахилої (малюнок 3). Проведемо пряму ![]() , паралельну прямій АВ. Вона перпендикулярна площині
, паралельну прямій АВ. Вона перпендикулярна площині ![]() . Проведемо через прямі АВ та
. Проведемо через прямі АВ та ![]() площину
площину ![]() . Пряма с перепендикулярна прямій
. Пряма с перепендикулярна прямій ![]() . Якщо вона перпендикулярна прямій СВ, то вона перпендикулярна площині
. Якщо вона перпендикулярна прямій СВ, то вона перпендикулярна площині ![]() , тобто, і прямій АС.
, тобто, і прямій АС.
Аналогічно, якщо пряма с перпендикулярна похилій СА то вона, будучи перпендикулярною і прямій ![]() , перпендикулярна площині
, перпендикулярна площині ![]() , а значить, і проекції похилій ВС. Теорему доведено.
, а значить, і проекції похилій ВС. Теорему доведено.
Того ж самого результату можна досягти, якщо скористатись координатним методом, попередньо задавши відповідні прямі їх напрямними векторами та послідовно використовуючи ознаки паралельності та перпендикулярності прямих у просторі.
Малюнок 2- Доведення теореми про три перпендикуляри.
5. Доведення методом координат ознаки паралельності двох площин.
Нехай завдані площини ![]() своїми рівняннями:
своїми рівняннями:
![]() (14)
(14)
![]() (15)
(15)
Оскільки координати загальної точки площин ![]() є розв’язанням системи рівнянь (14),(15) та кожне розв’язання системи рівнянь (14),(15) є координатами загальної точки площин
є розв’язанням системи рівнянь (14),(15) та кожне розв’язання системи рівнянь (14),(15) є координатами загальної точки площин ![]() , то питання про взаємне розташування двох площин
, то питання про взаємне розташування двох площин ![]() зводиться до дослідження системи лінійних рівнянь (14),(15).
зводиться до дослідження системи лінійних рівнянь (14),(15).
Позначимо через r та ![]() відповідно ранги матриць:
відповідно ранги матриць:
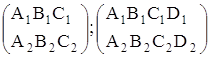
6. Рівняння сфери. Властивість перетину кулі площиною.
Знайдемо рівняння сфери радіуса r з центром С (a, b, c) в прямокутній системі координат. Точка М простору належить цій сфері тоді та тільки тоді, коли СМ=r або СМ2=r2. Ця рівність в координатах запишеться таким чином:
![]() (16 )
(16 )
Це – рівняння сфери радіусу r з центром в точці С (a, b, c). Зокрема якщо центр сфери співпадає з початком координат, то a=b=c=0, тому рівність ( 16 ) набуває вигляду :
![]() (17 )
(17 )
Рівняння (16) можна записати у вигляді :
![]() (18 )
(18 )
де
![]()
Таким чином, рівняння будь- якої сфери в прямокутній системі координат має вигляд (18 ). За аналогією з колом можна довести, що якщо коефіцієнти рівняння (18) задовольняють нерівності ![]() , то поверхня, задана цим рівнянням є сфера з центром
, то поверхня, задана цим рівнянням є сфера з центром ![]() та радіусом
та радіусом 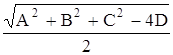 . Перетин кулі площиною є коло- основна властивість перетинів кулі площиною.
. Перетин кулі площиною є коло- основна властивість перетинів кулі площиною.
При написанні курсової роботи при розгляді питань широко використовувався метод координат. Були розглянуті питання прямої та площини у просторі, умови взаємного розташування прямої та площини, умови паралельності та перпендикулярності прямих та площин.
Список використаної літератури1. Атанасян Л.С.,Базылев В.Т. Геометрия. В 2-х ч.. Ч.1.- М.: Просвещение,1986.-336 с.
2.Погорелов А.В. Геометрия.-М.:Наука,1983.-288 с.
3. Атанасян Л.С., Атанасян В.А. Сборник задач по геометрии, ч.1.-М.:Просвещение,1974.
4. Мальцев А.И. Основы линейной алгебры.-М.: Наука,1970.
Похожие работы
... враховуючи їх невелику кількість у підручниках, посібниках та майже повну відсутність серед добірок завдань контролюючого характеру. 2.2 Загальні методичні рекомендації вивчення елементів стереометрії у курсі геометрії 9 класу 2.2.1 Формування уявлень і понять про стереометричні фігури та деякі їх властивості Формування понять – складний психологічний процес, який починається з утворення ...
... метод координат. V. Аксіома паралельності Сама остання аксіома грає в геометрії особливу роль, визначаючи поділ геометрії на дві логічно несуперечливі й взаємно виключають один одного системи: Евклідову й неевклідову геометрії. У геометрії Евкліда ця аксіома формулюється так. V. Нехай а – довільна пряма й А – крапка, що лежить поза прямій а, тоді в площині α, обумовленою крапкою А и ...


0 комментариев