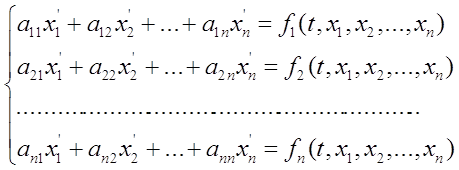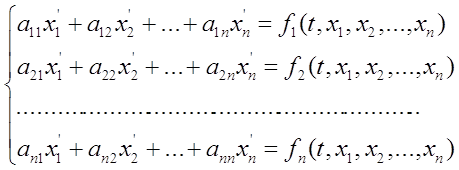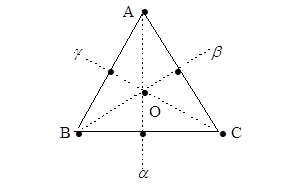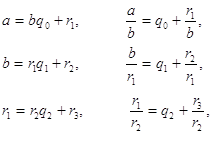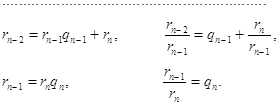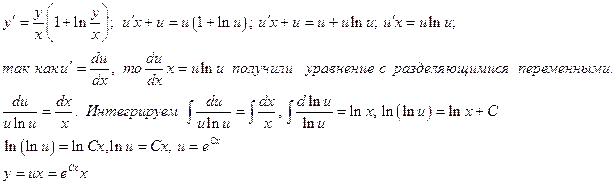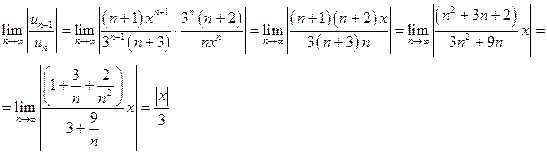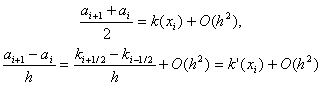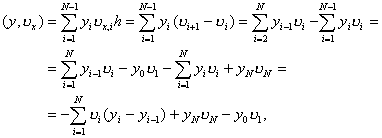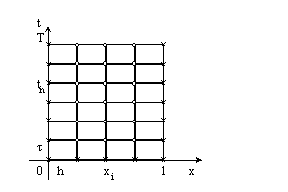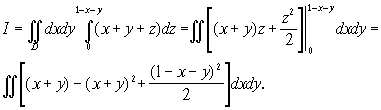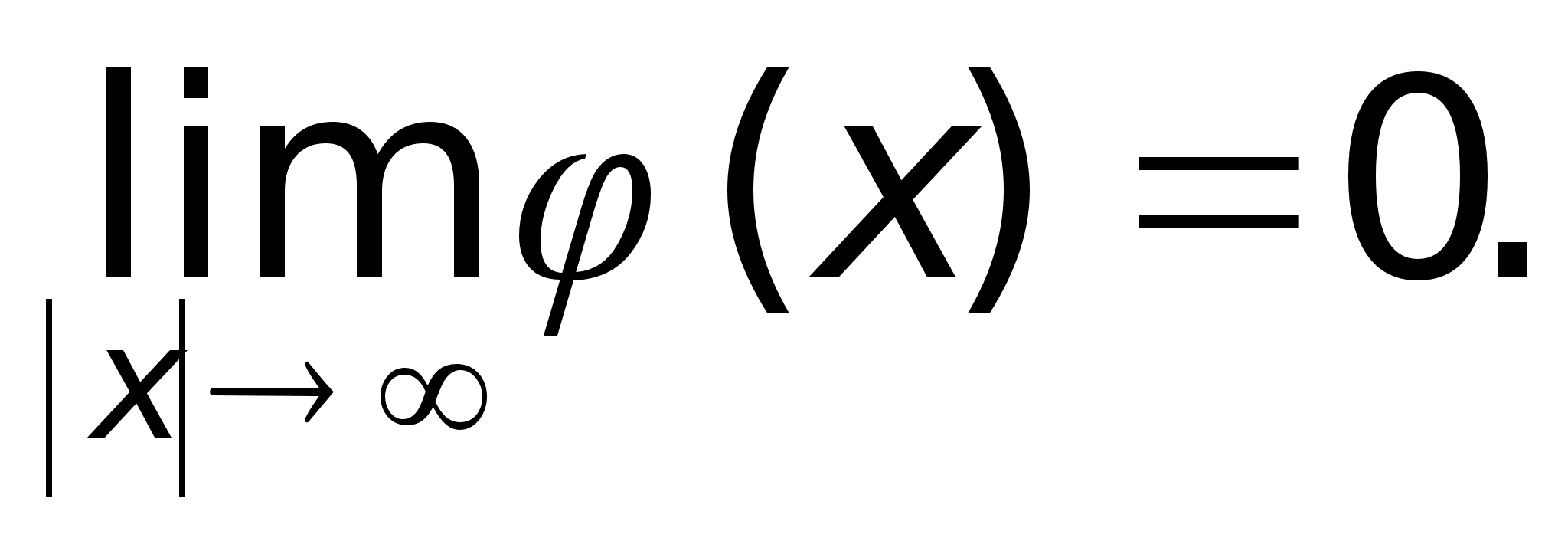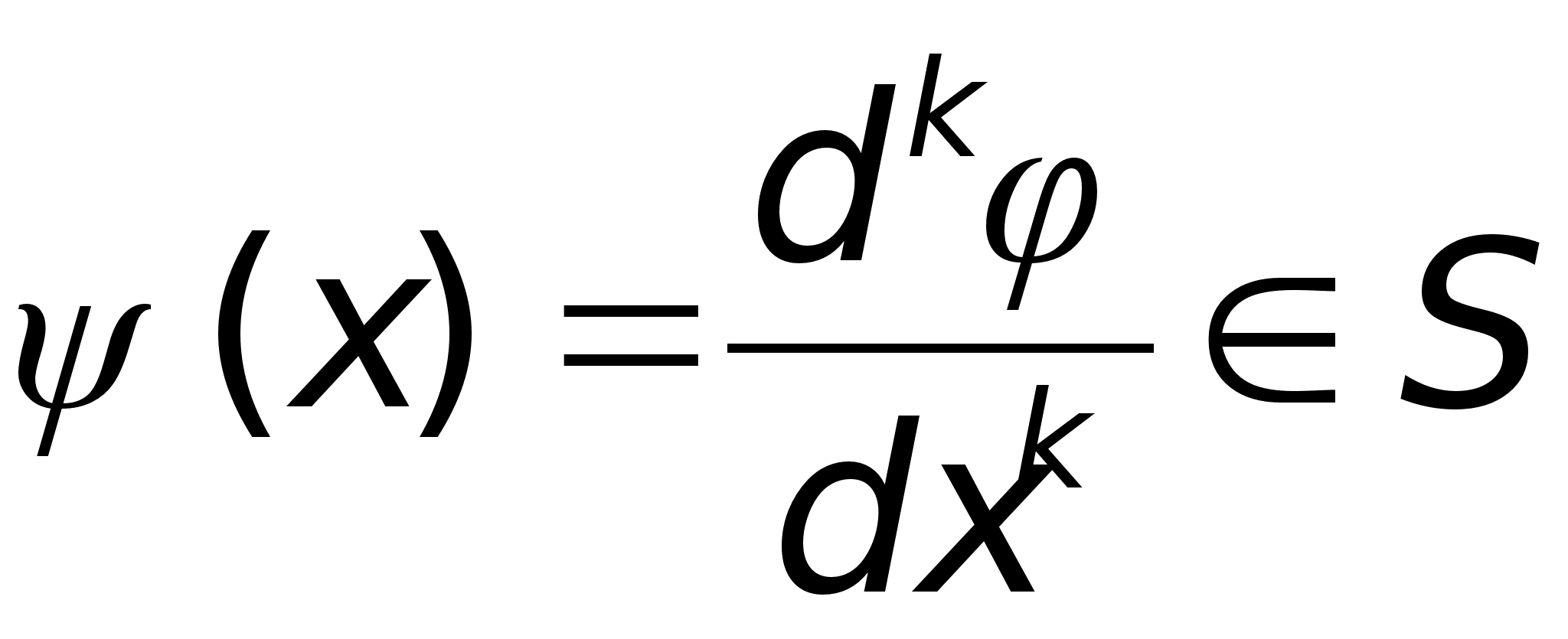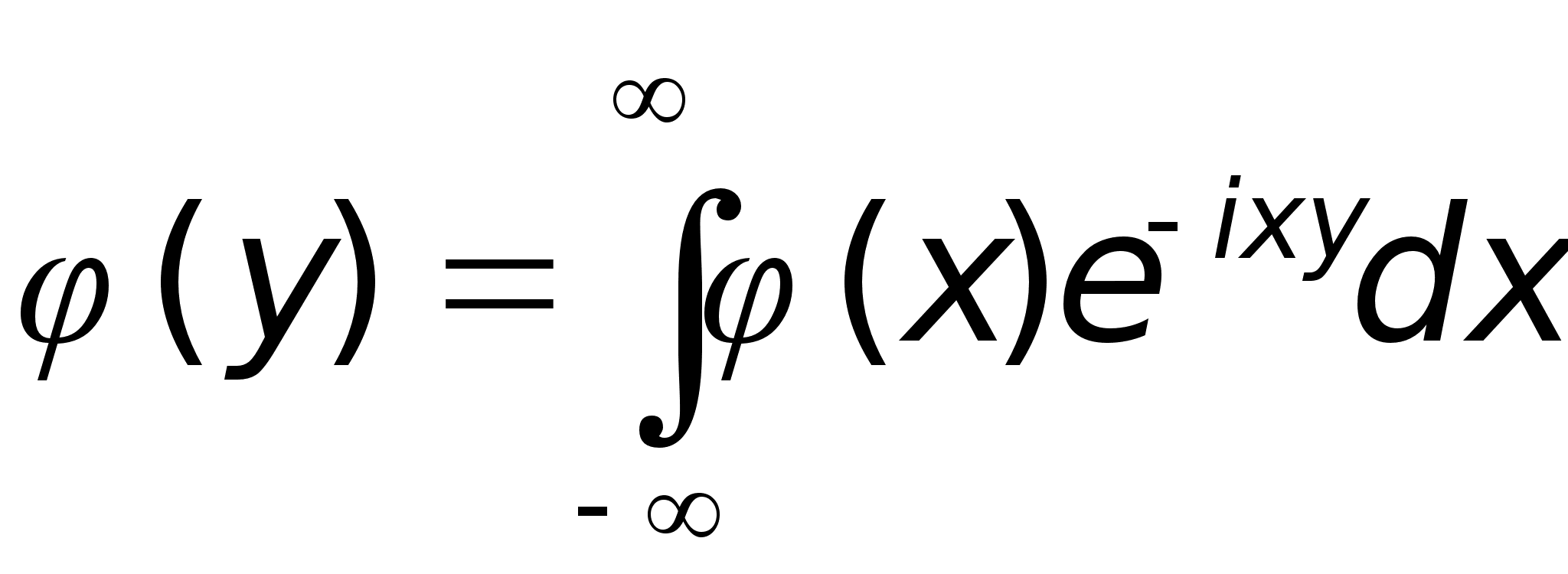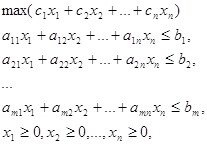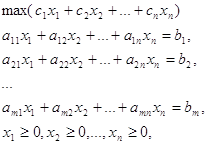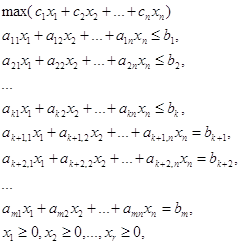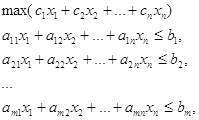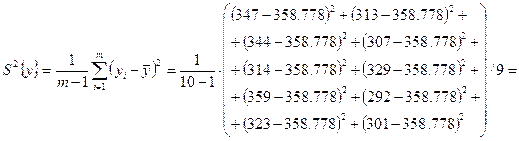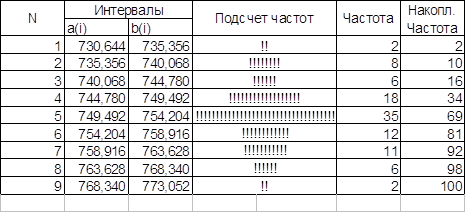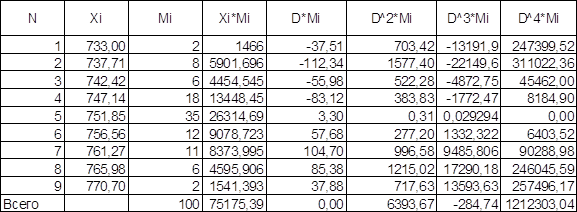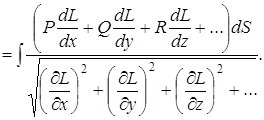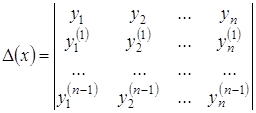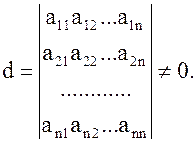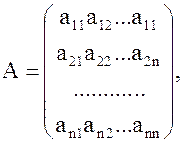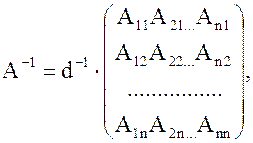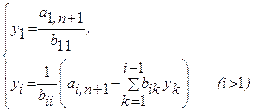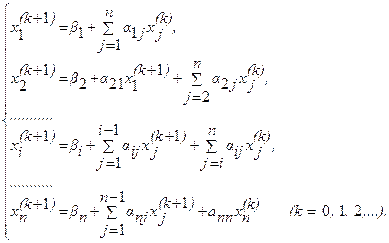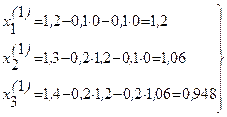| № | Название работы | Скачать |
|---|---|---|
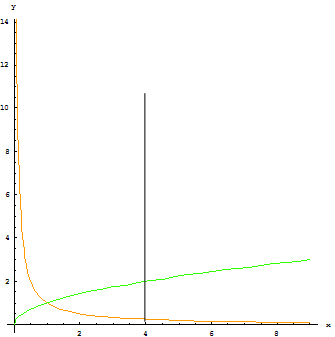
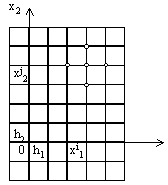
| 2201. |
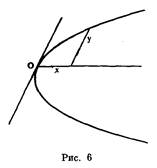
Развитие аналитической геометрии ... ED, GF, а пятая GA к ним перпендикулярна (рис. 9), причем CF·CD·CH = СВ·СМ·а, где а — расстояние между соседними эквидистантами. Здесь появляется первое в истории аналитической геометрии уравнение кривой третьего порядка. Обозначив СВ = у, СМ = х, Декарт находит у3 — 2ay2 — аау + 2а3 = аху, т. е. ... |
|
| 2202. |
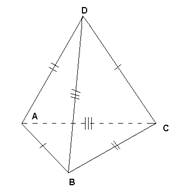
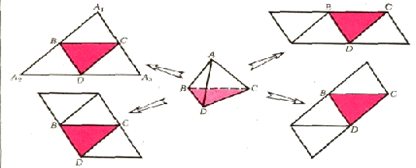
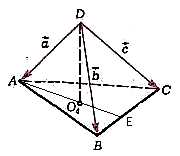
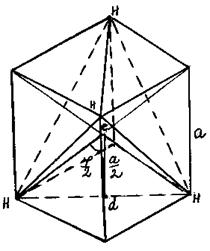
Равногранный тетраэдр ... рис. 4). (21) Сумма косинусов всех двугранных углов равна 2. Все перечисленные условия являются одновременно и свойствами и признаками равногранного тетраэдра. Чтобы вывести равногранность из какого-нибудь условия, надо выстроить целую цепочку промежуточных условий, в которой каждое прямое ... |
|
| 2203. |
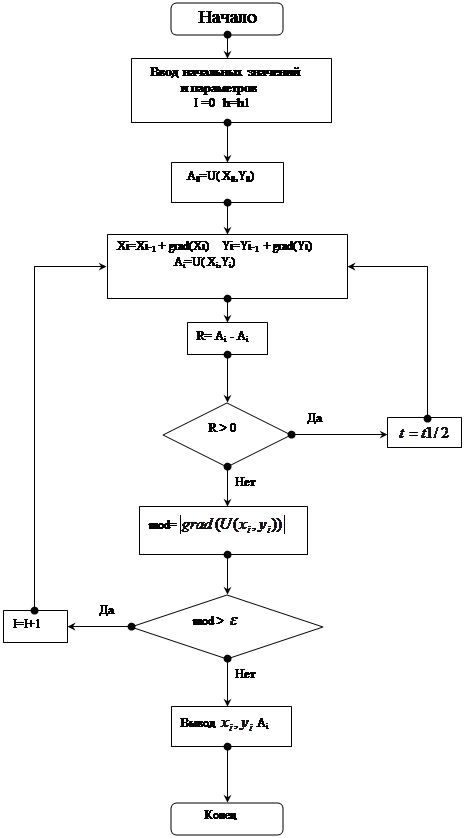
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЯТИТОЧЕЧНЫМ МЕТОДОМ АДАМСА – БАШФОРТА ... трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . ... |
|
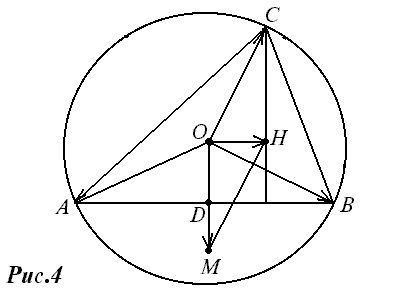
| 2204. |
Прямая Эйлера ... , высоты треугольника ABC пересекаются в точке H, определяемой соотношением (3). Легко проверить, что теорема 2 справедлива и для прямоугольного треугольника. Прямая Эйлера. Из доказанных теорем 1 и 2 вытекает интересующее нас свойство замечательных точек треугольника. Теорема 3. Центр О ... |
|
| 2205. |
Простые числа Мерсенна. Совершенные числа ... Числа Р2=6 и Р3=28 были известны ещё пифагорейцам. Числа Р5=496 и Р7=8128 нашел Евклид. Используя другие простые числа Мерсенна и формулу 4, находим следующие совершенные числа: 6)Р13=33550336, Р17=8589869056, Р19=137438691328, Р31=2305843008139952128. Для всех остальных чисел Мерсенна числа Рр ... |
|
| 2206. |
Производная и ее применение в алгебре, геометрии, физике ... ; Для доказательства неравенств. Рассмотрю некоторые примеры применения производной в алгебре, геометрии и физике. Задача 1. Найти сумму 1+2*1/3+3(1/3)2+…+100(1/3)99; Решение. Найду сумму g(x)=1+2x+3x2+…+100x99 и подставлю в нее ... |
|
| 2207. |
Проективная геометрия ... гармонические. Как и свойство взаимной раздельности пар, свойство гармонической сопряжённости инвариантно относительно проектирования (это инвариант проективной геометрии) (рис.14). Т. e. если P, Q и S, T гармонически сопряжённые пары, то после проектирования из некоторого центра O на прямую и ... |
|
| 2208. |
Программа государственного экзамена по математике для студентов математического факультета Московского городского педагогического университета ... ; . . . . . . . . . . . . . rn-2 = rn-1 qn-1 + rn . Докажем, что каждое из чисел rk линейно выражается через a и b с целыми коэффициентами. Для r1 утверждение тривиально: r1 = a - bq1 . Считая, что каждое из чисел r1 , r2 , . . . , rn-1 является целочисленной линейной ... |
|
| 2209. |
Принятие решений в условиях неопределенности ...
i3
= 17.5, i4
= -1.
Теперь из чисел
3, 12, 17.5, -1 берем максимальное.
Это — 17.5. Значит,
правило Гурвица
рекомендует
3-е решение.
Принятие
решений в условиях
частичной
неопределенности.
Предположим,
что в рассматриваемой
схеме известны
вероятности
pj
того, что
реальная ситуация
развивается
по ... |
|
| 2210. |
Примеры решения ... из исходного делением обеих частей на . Ответ: Составляем характеристическое уравнение тогда Ответ: 83 Исследовать сходимость числового ряда. Решение: . В этом задании и Применим признак Даламбера. Найдем , так то ряд расходится по признаку Даламбера. Ответ: ряд расходится. ... |
|
| 2211. |
Разностные аппроксимации ... сетки, а именно в точках (x1i, x2j), (x1i± 1, x2j), (x1i, x2 j± 1). Указанное множество точек называется шаблоном разностного оператора. Возможны разностные аппроксимации оператора Лапласа и на шаблонах, содержащих большее число точек. 2. Исследование аппроксимации и сходимости 2.1. Аппроксимация ... |
|
| 2212. |
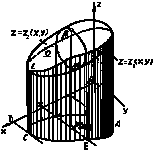
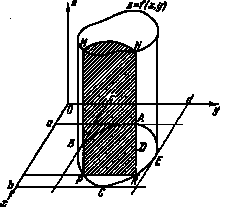
Тройные и кратные интегралы ... интегрировать сначала по направлению оси Oy, а затем по области плоскости Oxz), то это приведёт к изменению порядка интегрирования в тройном интеграле и к изменению пределов интегрирования по каждой переменной. Рис.3 Рис.4 А) Пример. Вычислим тройной интеграл где - ... |
|
| 2213. |
Применение информатики, математических моделей и методов в управлении ... широкого
перечня алгоритмов,
применяющихся
в планировании
и других экономических
расчетах. IV. Заключение
Как видно из
всего вышесказанного,
значение
математических
моделей и информатики
в управлении
велико. В ближайшие
10 лет мир изменится
сильнее, чем
за предыдущие
50. И от того, насколько
... |
|
| 2214. |
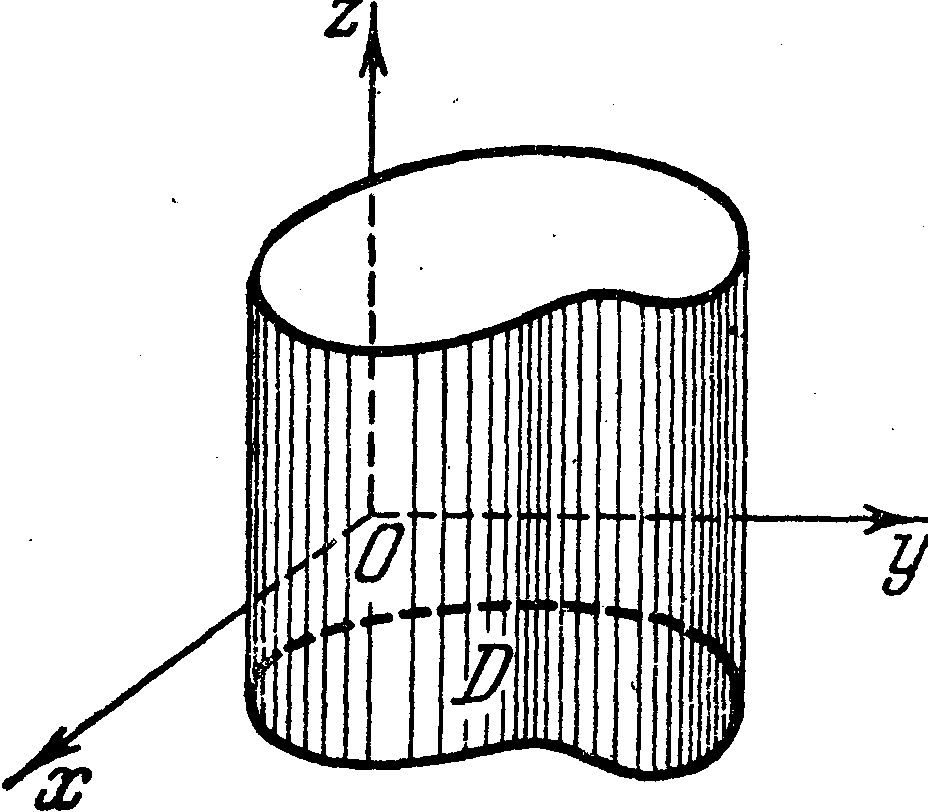
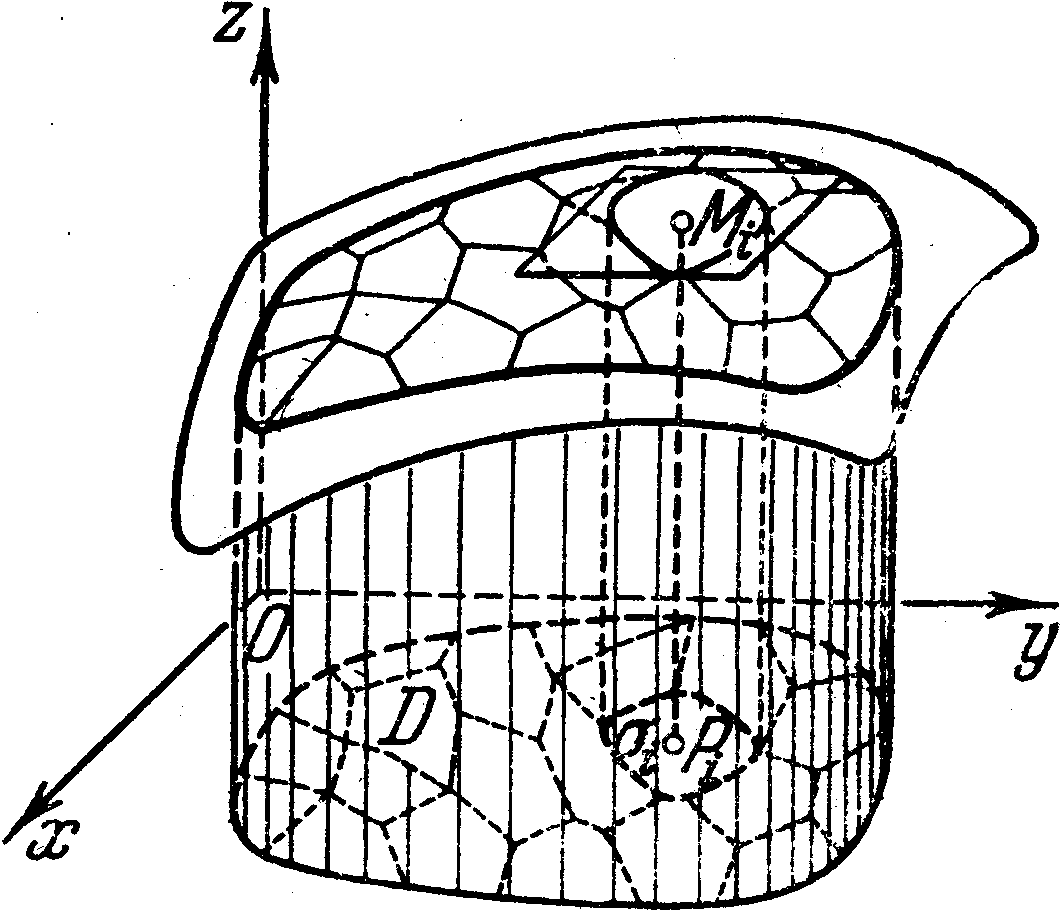
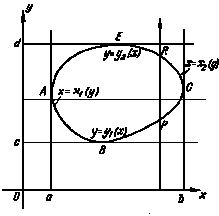
Двойной интеграл в механике и геометрии ... интегрировании считается величиной постоянной. Интегрируя затем Q(у) в пределах изменения у, т. е. от c до d, мы придем ко второму выражению для двойного интеграла (Б) Здесь интегрирование совершается сначала по х, а потом по у. .Формулы (А) и (Б) показывают, что вычисление двойного интеграла ... |
|
| 2215. |
Применение алгоритма RSA для шифрования потоков данных ...
проектирования
перед студентом
Малышевым А.А.
была поставлена
задача: на основе
алгоритма RSA
для шифрования
блоков данных,
построить
алгоритм и
реализовать
программный
продукт для
шифрования
потоков данных.
В результате
выполнения
дипломного
проектирования
был составлен
принципиальный
алгоритм ... |
|
| 2216. |
Приложения производной ... .
Такие уравнения,
содержащие
производные,
называются
дифференциальными.
В своей
же работе я
хочу подробнее
остановится
на приложениях
производной.
1. Понятие
производной
При
решении различных
задач геометрии,
механики, физики
и других отраслей
знания возникла
необходимость
с помощью одного
и ... |
|
| 2217. |
Прикладная математика ... объяснить при защите курсовой работы!) и найдите по ней худшую и лучшую операции. 18. Произвести математико-статистический анализ за T лет Xt, Kt, Lt
(t = 1, …, T) о выпуске продукции (в стоимостном виде), ОПФ и числе занятых исследуемого производственного экономического ... |
|
| 2218. |
Приближенный метод решения интегралов. Метод прямоугольников (правых, средних, левых) ... f(x) задана графически или таблицей, то для вычисления определенного интеграла применяют приближенные формулы. Для приближенного вычисления интеграла можно использовать метод прямоугольников (правых, левых, средних). При вычислении интеграла следует помнить, каков геометрический смысл определенного ... |
|
| 2219. |
Приближенное решение уравнений методом хорд и касательных ... . Следует отметить, что обе функции непрерывны и дважды дифференцируемы на всей области определения (–¥ ; ¥). Необходимо найти приближенные решения уравнений с заданной точностью (0,001). С целью упростить работу (в частности, избавить человека от однотипных арифметических и логических ... |
|
| 2220. |
Приближенное решение уравнений ...
простого по
виду уравнения,
как: х^5-4х-2=0 Сказанное,
однако, не означает
отсутствия
в науке методов
решения уравнения
высших степеней.
Имеется много
способов
приближенного
решения уравнений
- алгебраических
и неалгебраических
(или, как их
называют,
трансцендентных),
позволяющих
вычислять их
... |
|
| 2221. |
Приближенное вычисление определенных интегралов труднительно, и применяются различные способы вычисления определенных интегралов. Один из них приведен ниже. Формула парабол (формула Симпсона) Разделим отрезок [a,b] на четное число равных частей n = 2m. Площадь криволинейной трапеции, соответствующей первым двум отрезкам [x0,x1] и [x1,x2] и ... |
|
| 2222. |
Приближенное вычисление определенного интеграла при помощи квадратурной формулы Чебышева ... и выводы.
Таким образом
очевидно, что
при вычислении
определенных
интегралов
с помощью квадратурных
формул, а в частности
по формуле
Чебышева не
дает нам точного
значения, а
только приближенное.
Чтобы максимально
приблизиться
к достоверному
значению интеграла
нужно уметь
правильно
выбрать метод
и ... |
|
| 2223. |
Приближённые методы решения алгебраического уравнения ... . 5. Метод касательных (метод Ньютона)
Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f & ... |
|
| 2224. |
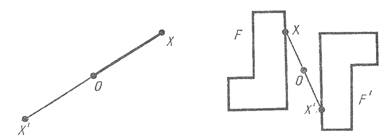
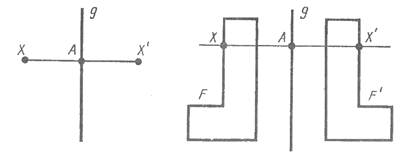
Преобразования фигур ... O. Точка, симметричная точке O, есть сама точка O. Очевидно, что точка, симметричная точке X', есть точка X. Преобразование фигуры F в фигуру F', при котором каждая ее точка X переходит в точку X', симметричную относительно данной точке O, называется преобразованием симметрии относительно ... |
|
| 2225. |
Преобразования плоскости, движение ... X перешла в X'. Тогда угол XOX'=180 градусов, как развернутый, и XO=OX', следовтельно такое преобразование является поворотом на 180 градусов. Отсюда также следует, что центральная симметрия является движением. Центральная симметрия является движением, изменяющим направления на противоположные.То ... |
|
| 2226. |
Преобразование Фурье ...
4) функция (1+x2)S(R)
и, следовательно,
ограничена,
а (1+x2)-1L1(R).
Поэтому функция
(1+x2)(1+x2)-1L1(R).§3.
Свойства
преобразований
Фурье функций
из S(R).
1)
Доказательство
получается
дифференцированием
в (1) под знаком
интеграла. Это
законно, так
как ... |
|
| 2227. |
Представление чисел в виде суммы двух квадратов и ... ... натуральное число (r0, ибо иначе пары были бы одинаковы). С другой стороны, a2+b2 2[]2<2p, т. е. r=1, и значит, a2+b2=p. Теорема
доказана. Вопрос о представлении чисел в виде суммы двух квадратов исчерпывается следующим утверждением: Натуральное число представимо в виде суммы двух квадратов ... |
|
| 2228. |
Пределы ... N0,
n>N0 |Xn|>M
=>n>N0.
|Yn|=1/|Xn|Yn – б.м. => lim Yn=0 (n).
3.Сумма
б.б величины
и ограниченной
есть б.б. величина.
Основные
теоремы о пределах: lim Xn=a, lim Yn=b => lim (XnYn)=ab (n)
Док-во:
lim Xn=a => Xn=a+n;
... |
|
| 2229. |
Практикум по предмету Математические методы и модели ... конструктивной безопасности строящихся зданий и сооружений // Известия ВУЗов. Строительство.–2000.–№ 2-3.–С. 114 – 117. Шепелев И.Г. Математические методы и модели управления в строительстве.–М.:Высшая школа, 1980. Приложение
1Таблица
П1. F-распределение
Фишера
Значения F ... |
|
| 2230. |
Практика перевода числа из одной системы счисления в другую + блок-схема алгоритма определения наименьшего числа ... 27816 = 11708 984,65210=1111011000,10011110002=3D8, 27816=1730,11708 23674,56677510=57CA,8A5F716=56172,21227678 = = 101110001111010,100010100101111101112 Задание №1, вопрос №5: Перевести заданные в одной системе счисления числа в другую указанную в скобках систему счисления. А) 333,13 8 (8 - 2 |
|
| 2231. |
Правильные многогранники или тела Платона ... в диалоге "Пир" выдвигается понятие
предела; идея выступает здесь как предел становления вещи. ТЕЛА ПЛАТОНА. Тела Платона-это выпуклые многогранники, все грани которых правильные многоугольники. Все многогранные углы правильного многогранника конгруэнтны. Как это следует уже из подсчета ... |
|
| 2232. |
Правильные многогранники ... куб), правильный октаэдр, правильный додекаэдр и правильный икосаэдр. К этому заключению можно прийти несколько иначе. Действительно, если грань правильного многогранника – правильный треугольник, и в одной вершине сходятся k ребер, т.е. все плоский углы выпуклого k-гранного угла равны , то . ... |
|
| 2233. |
Правила по отношению к аргументам и ошибки, с ними связанные ... области положения. 4. Роль аргументов могут выполнять определения основных понятий конкретной области знаний. ПРАВИЛА И ОШИБКИ ПО ОТНОШЕНИЮ К АРГУМЕНТАМ. Логическая состоятельность и доказательное значение рассуждения во многом зависит от качества исходного фактического и теоретического ... |
|
| 2234. |
Похідна функції, правила диференціювання ... похідну y’ для функції y=y(x),заданої параметрично. Вправа №19(6) Знайти похідну для функції, заданої параметрично. Вправа №20(4) Знайти похідну для диференційованої функції, заданої неявно рівнянням: Розв”язок: Вправа №21(1) Знайти для функції ліву і праву похідні в точці х0. Вправа №21(3) Зн |
|
| 2235. |
Похідна та її застосування ... ї монотонності застосовується похідна. Використовують і такий факт: якщо многочлен k-го степеня має k дійсних коренів, то його похідна має їх k –1 . Розглянемо застосування похідної до розв’язування рівнянь на конкретних прикладах. Приклад 1. Яким умовам повинні задовольняти параметри p та q, щоб ... |
|
| 2236. |
Построение решения задачи Гурса для телеграфного уравнения методом Римана ератор, формула Гріна, функція Рімана. Мета роботи: в даній роботі необхідно ознайомитись з методом отримання розв’язку задачі Гурса для телеграфного рівняння (1.1) з початковими умовами (1.2); довести існування та єдиність цього розв’язку; навести приклади та вказати області вживання цього ... |
|
| 2237. |
Построение приближенного решения нелинейного уравнения методом Ван-дер-Поля ... использовать малые нелинейности, однако даже при малых нелинейностях получившаяся задача не допускала интегрирования колебаний в квадратурах. Ван-дер-Поль разработал приближенный асимптотический метод интегрирования дифференциальных уравнений второго порядка подобного рода. 1.1. Метод усреднения ... |
|
| 2238. |
Построение линии пересечения 2-х конусов и цилиндра ...
луча j=0;
ветвь, соответствующая
знаку «-»
в формуле
(IX),
посторонняя. Описание линии пересечения конусов на выкройке первого конусаПодставляя
параметризацию
первого конуса
(IX),
в уравнение
второго конуса(V),
получаем
уравнение:
(rsinbcos+7.7)2tg2b=(-7.7+rcosb)2+r2sin2bsin2 квадратное
... |
|
| 2239. |
Построение кубического сплайна функции ... [index]; delete [] tmp; for (i = 1; i <= n; i++) { d(i) = y[i-1]; a(i) = (b(i+1)- b(i))/(-3*step); c(i) = (y[i] - d(i) - pow(step,2)*b(i) + pow(step,3)*a(i) )/(-step); } i=0; //построение графика сплайна при помощи полученный коэф-тов (см. выше) for (i=0; i < n; i++) for (int ... |
|
| 2240. |
Построение графика функции различными методами (самостоятельная работа учащихся) ... все методы обучения, воспитывать в учениках потребность самостоятельно добывать знания, умение творчески пользоваться объяснениями учителя, помощью товарищей, книгами, конспектами одна из важнейших целей нашей работы.ГЛАВА 2. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИЙ
ПРИЁМЫ И МЕТОДЫ §1. ... |
|
| 2241. |
Постановка задачи линейного программирования и двойственная задача линейного программирования. ... с любым другим допустимым вектором , т.е. , называется решением задачи, или оптимальным планом. Максимальное значение целевой функции называется значением задачи. Двойственная задача линейного программирования. Рассмотрим задачу ЛП (1) или, в матричной записи, (2) Задачей, двойственной к ... |
|
| 2242. |
Пособие по планиметрии за 9-й класс льник, параллелограмм, трапеция, правильный n-уг |
|
| 2243. |
Понятие величины и её измерения в начальном курсе математики ... ГЛАВА 2.Методика формирования понятия величины и её измерения у младших школьников. 2.1 Современные подходы к изучению величин в начальном курсе математики. В начальных классах рассматриваются такие величины, как: длина, площадь, масса, объём ... |
|
| 2244. |
Полный курс лекций по математике ... комплексные числа, вводящие в рассмотрение «мнимое число» . История развития числа от целого числа до иррационального знакома нам по школьному курсу. С эпохи Возрождения математики стали использовать числа вида z = x+iy для решения квадратных уравнений, дискриминант у которых отрицателен, где i ... |
|
| 2245. |
Поиск клик в графах ... ; {конец пеpебоpа возможных мест в стpоке} end; {конец пpохода по стpокам} close(fileklics); end; Выше представлена процедура нахождения клик в графе. Описание переменных: StolbecSravn: номер сравниваемого столбца. StringSravn: номер текущей строки. Num ,i1,i: счетчики. lenStolb: размер множества ... |
|
| 2246. |
Поверхности второго порядка ... (19) которое является уравнением параболического цилиндра с образующими, параллельными новой оси Ох. § 3. Исследование формы поверхностей второго порядка по их каноническим уравнениям 1. Эллипсоид. Из уравнения (3) вытекает, что координатные плоскости являются плоскостями симметрии ... |
|
| 2247. |
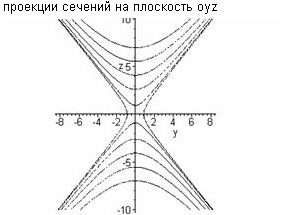
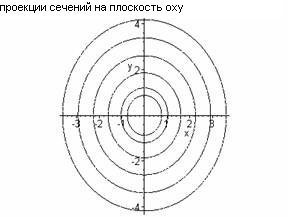
Поверхности второго порядка ... – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых и точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами. 6. Конус второго порядка. Конусом второго порядка называется поверхность, которая в некоторой |
|
| 2248. |
Определенный интеграл ... неопределенным интегралом. Это понятие выделил Лейбниц, который заметил, что все первообразные функции отличаются на произвольную постоянную. А называют определенным интегралом (обозначение ввел К. Фурье (1768-1830), но пределы интегрирования указывал уже Эйлер). Самое важное из истории ... |
|
| 2249. |
Математическое моделирование при решении экологических задач ... роль в решении проблемы сохранения жизни на Земле играет математика с ее методом математического моделирования. Итак, при объяснении метода математического моделирования и его применения к решению экологических задач реализуется практическая направленность обучения, поскольку математический метод ... |
|
| 2250. |
План чтения лекции по учебной дисциплине «Математические методы» ... «опорной точкой», а вытекающее из неё решение «опорным решением». Отсюда вытекает идея, лежащая в основе большинства рабочих методов решения ОЗЛП, - идея «последовательных проб». Действительно, попробуем разрешить уравнения (7.1.) относительно каких–нибудь m базисных переменных и выразим ... |
|
| 2251. |
Плёночные и гибридные интегральные схемы ... катушки диэлектрическую пленку, а затем поверх этой пленки наносить металлическую пленку — вывод. III. Гибридные ИС. Широкое распространение получили гибридные ИС – интегральные схемы, в которых применяются плёночные пассивные элементы и навесные элементы (резисторы, конденсаторы, диоды, оптроны, ... |
|
| 2252. |
Пирамида и призма ... Вершины Рёбра Тетраэдр 4 4 6 Куб 6 8 12 Октаэдр 8 6 12 Додекаэдр 12 20 30 Икосаэдр 20 12 30 Призма n-угольная 2n 3n n+2 Пирамида n-угольная n+1 2n n+1 Теорема Эйлера. Для числа граней Г, числа ... |
|
| 2253. |
Пирамида ... спектру частот, часть которых идентична частотам колебаний здоровых клеточных структур биологических объектов, излучением пирамиды оказывается гармонизирующее, натраивающее на оптимальное функционирование воздействие. Французскими радиэстезистами Л.Шомери и А. де Белизалом(1976) впервые было ... |
|
| 2254. |
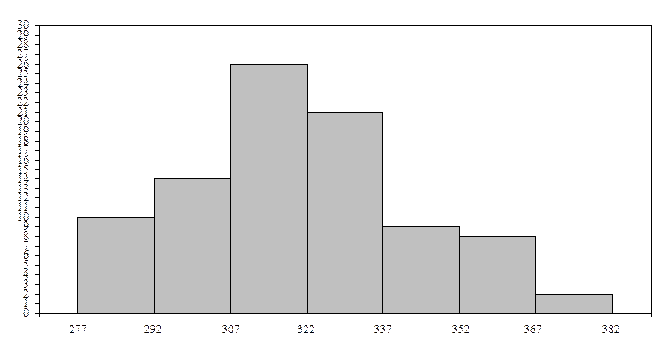
Первичная статистическая обработка информации ... 280 395 Путем статической обработки результатов измерений выполнить следующие пункты задания: Задание 1. Первичная статистическая обработка информации. 1. Построить вариационный статистический ряд. 2. Определить размах колебаний вариант. 3. & ... |
|
| 2255. |
Первая краевая задача для уравнения теплопроводности в нецилиндрической неограниченной области ...
0.
t
x Требуется
привести пример
оценки решения задачи (З) в
области
, и исследовать
полученную
оценку при 2. Оценочный
анализ решения
задачи.
Оценка решения
задачи (З) основывается
на принципе
максимума для
уравнения
теплопроводности
: «Всякое решение
уравнения
в прямоугольнике
, непрерывное
... |
|
| 2256. |
Пафнутий Львович Чебышев ... в университет, Чебышевы в 1832 году переехали в Москву. Для занятий с детьми были приглашены лучшие учителя. В 1837 году шестнадцатилетний Пафнутий Чебышев становится студентом физико-математического отделения философского факультета Московского университета, отлично учился, в 1847 году с отличием ... |
|
| 2257. |
Оценочный и сравнительный эксперимент ... и находятся в пределах интервала (; ), следовательно резко выделяющихся значений в выборке нет. 2. Обработка сравнительного технологического эксперимента. Подготовка данных: сформировать из исходного массива В1 методом рандомизации две выборки малого объёма В2 и В3 для ... |
|
| 2258. |
Оценка вероятности безотказной работы по критериям остаточного ресурса ... в области D[l,t,l*]: (16) Другую эквивалентную форму получим, взяв в качестве независимой переменной l*: (17) Рассмотренная схема оценки вероятности отказов по критерию остаточного ресурса учитывает рост одиночного дефекта. При наличии множества начальных дефектов с различными размерами ... |
|
| 2259. |
Оценивание параметров и проверка гипотез о нормальном распределении (WinWord, Excel) ... : Построенные графики находятся в приложениях к работе. 6* Проверить гипотезу о нормальном законе распределения по критерию согласи яПирсона f^2). Проверка гипотез о нормальном законе распределения Частоты для проверки соответствия эмпирического ряда распределения нормальному закону ... |
|
| 2260. |
Остроградский ... и интеграл по ограничивающей ее сверхповерхности S с уравнением L(x,y,z,…)=0. Если придерживаться прежних обозначений, то формула имеет вид (3) Впрочем, Остроградский не применял геометрических образов и терминов, которыми пользуемся мы: геометрия многомерных пространств в то время еще не ... |
|
| 2261. |
Основные понятия и решения моделирования ... Учебные вопросы и расчет времени №п/п Учебные вопросы Время, мин Методические указания 1. 2. 3. 4. Введение. Оптимальное решение. Основные понятия и определения оптимизации. Постановка задачи оптимизации в общей форме. 1. Вводная часть. ... |
|
| 2262. |
Основные понятия дифференциального исчисления и история их развития (Бакалавр) ... [х ln х] – [х] = 2 ln2 – 1 = ln4 – 1 3.Исторические сведения о возникновении и развитии основных понятий. В математике XVII в. самым большим достижением справедливо считается изобретение дифференциального и интегрального исчисления. Сформировалось оно в ряде сочинений Ньютона и Лейбница и их ... |
|
| 2263. |
Основные определения и теоремы к зачету по функциональному анализу ... : Компактный
(вполне непрерывный)
оператор –
замкнутый шар
пространства
X переводит
в замкнутый
шар пространства
Y.
Определение: (X,Y) –
подпространство
компактных
операторов
Теорема: Шаудера. A(X,Y)
A*(X*,Y*)
Линейные
нормированные
пространства ... |
|
| 2264. |
Организация познавательной деятельности учащихся на факультативных занятиях по теме Иррациональные неравенства ... форм,
разработана
методика применения
самостоятельной
работы вместе
с иными формами
организации
познавательной
деятельности
на факультативных
занятиях в
выпускных
классах средней
школы, изучены
учебные возможности
учащихся в
экспериментальной
группе, проведена
опытно- экспериментальная
работа по ... |
|
| 2265. |
Построение математических моделей при решении задач оптимизации ... котором задаются математические соотношения, связывающие исходные данные и результат. В этом случае говорят о построении математической модели задачи. Обычно модель возникает как необходимый этап решения конкретной задачи. Однако в дельнейшем может происходить обособление модели от задачи, и модель ... |
|
| 2266. |
Определение рационального варианта размещения производственно-хозяйственных предприятий (на примере АБЗ) и выбор оптимального маршрута поездки коммивояжера ... последний разрешающий элемент. В итоге искомый маршрут будет проходить через пункты: А – Б – Г – Д – В – А min z = 16+21+16+12+13 = 78 Раздел 2. Определение рационального варианта размещения производственных предприятий (на примере АБЗ). Постановка задачи: В 2000г планируется ... |
|
| 2267. |
Определение законов распределения случайных величин и их числовых характеристик на основе опытных данных. Проверка статистических гипотез ... значимости =0,05 и числу степеней свободы 8-3=5 находим Т.к. , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины . Для случайной величины : Используя предполагаемый закон распределения, вычислим теоретические частоты по формуле , где - ... |
|
| 2268. |
Операторы в вейвлетном базисе ... вычислением следующих выражений: (4.1) (4.2) (4.3) 4.1 Оператор d/dx в вейвлетном базисе Нестандартные формы некоторых часто используемых операторов могут быть вычислены явно. ... |
|
| 2269. |
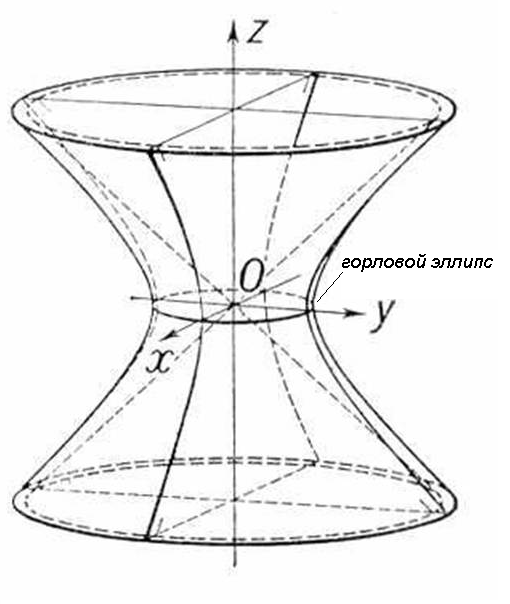
Однополостный гиперболоид ... определяется уравнением (1) Из уравнения (1) вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат — центром симметрии однополостного гиперболоида. Уравнение (1) называется каноническим уравнением однополосного гиперболоида. ... |
|
| 2270. |
Обработка результатов экспериментов и наблюдений ... результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы 1. Цель математической обработки результатов эксперимента; 2. Виды измерений; 3. Типы ошибок измерения; 4. Свойства случайных ошибок; 5. Почему среднеарифметическое ... |
|
| 2271. |
Обеспечение надежности функционирования КС ...
опасные и жизненно
важные технологические
процессы
автоматизированы
с использованием
вычислительной
техники. Это
приводит к
необходимости
обеспечения
высокой надежности
и эффективности
таких систем.
В данной
работе отражаются
основные принципы
и методы расчета
надежности
автоматизированных
систем ... |
|
| 2272. |
Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам Дирихле ... получим две интегральные формулы Пуассона для кругового кольца: ,
(82) ,
(83) где (74) и (75) – реальные и мнимые части компактной интегральной формулы Вилля-Шварца для кругового кольца [2], - функция Вейерштрасса, - угол наклона касательной к в точке , , - периоды, с – произвольная ... |
|
| 2273. |
Об алгебраических уравнениях высших степеней ... Лагранж (1736-1819) публикует в Мемуарах Берлинской Академии свой мемуар «Мысли над решением алгебраических уравнений», в котором делает критический пересмотр всех решений уравнений 3-й и 4-й степеней, данных его предшественниками, и замечает, что все они в сущности основаны на следующем принципе. ... |
|
| 2274. |
О неопределенных бинарных квадратичных формах ... Перейдем теперь к элементарному доказательству следующего результата. Теорема (Зигель). Для числа всех приведенных неопределенных бинарных квадратичных форм дискриминанта справедливо неравенство , где - произвольное положительное число, - постоянная, зависящая только ... |
|
| 2275. |
О некоторых применениях алгебры матриц ... из известных способов. §2. Применение циркулянтов малых порядков в теории чисел. Матрица вида: - называется циклической матрицей или циркулянтом (третьего порядка), а ее определитель – циклическим определителем. Циклическим определителем некоторые авторы называют также ... |
|
| 2276. |
Николай Иванович Лобачевский (1792 - 1856) ... меньше двух прямых, рано или поздно найдет своих ценителей. Многолетние плодотворные труды Лобачевского не могли получить положительной оценки у правительства Николая I. В 1846 г. Лобачевский оказался фактически отстраненным от работы в университете. Внешне он получил повышение - был назначен ... |
|
| 2277. |
Нечетко-логические модели и алгоритмы ... , как переход в другое пространство. В новом пространстве производится обработка нечетких переменных с использованием логических операций. В теории управления наиболее часто используется принцип максимина (алгоритм Мамдани). Затем полученный результат логической обработки с использованием обратного ... |
|
| 2278. |
Нестандартный анализ ...
переменного,
к теории групп
Ли, к гидродинамике
и теории упругости.
В 1966 г.
появилась
статья А.Р.
Бернстейна
и А. Робинсона,
в которой впервые
методами
нестандартного
анализа было
получено решение
проблемы инвариантных
пространств
для полиномиально
компактных
операторов.
В очерке П.Р.
Халмоша & ... |
|
| 2279. |
Некоторые дополнительные вычислительные методы ... приращения Dy: где Метод четвертого порядка для q = 3, имеет вид где Особо широко известно другое вычислительное правило Рунге-Кутта четвертого порядка точности: где Метод Рунге-Кутта имеет погрешность четвертого порядка (~ h4 ). Правило Рунге. Если приближенный метод имеет порядок ... |
|
| 2280. |
Некоторые Теоремы Штурма ... при каком t из отрезка , то при некотором t имеет место (3.32), и потому (3.32) справедливо на некотором подинтервале из . Но тогда на этом интервале и потому . Однако это противоречит условию . Доказательство закончено. Следствие 3.1 (теорема Штурма о разделении нулей). Пусть уравнение (3.12) ... |
|
| 2281. |
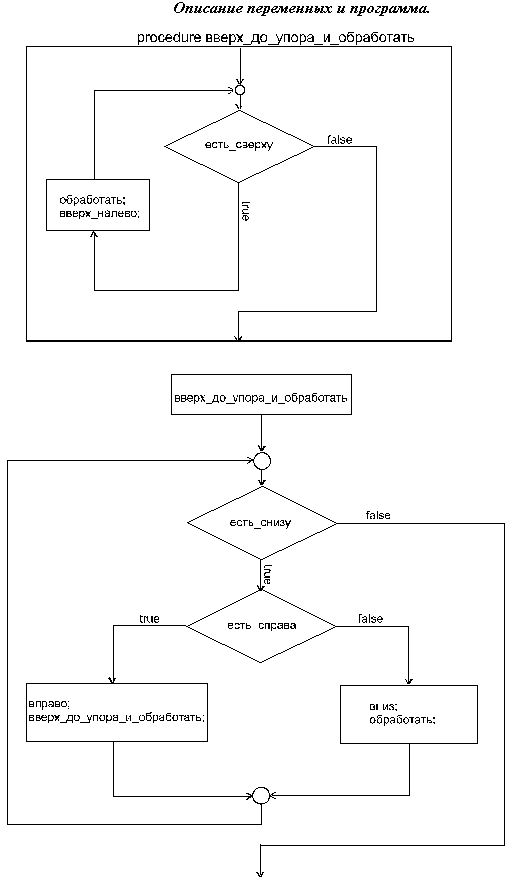
Математическая логика и теория алгоритмов ... есть_справа, есть_снизу} вниз; обработать; end; end; {ОНЛН, Робот в корне => все вершины обработаны полностью} Доказательство правильности алгоритма. Докажем, что приведенная программа завершает работу (на любом конечном дереве). Доказательство. Процедура вверх_налево завершает работу (высота ... |
|
| 2282. |
НАХОЖДЕНИЕ ВСЕХ ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ АЛГЕБРАИЧЕСКОГО МНОГОЧЛЕНА МЕТОДОМ ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ (БИСЕКЦИИ) И МЕТОДОМ ХОРД И КАСАТЕЛЬНЫХ С УКАЗАННОЙ ТОЧНОСТЬЮ И УЧЕТОМ ВОЗМОЖНОЙ КРАТНОСТИ КОРНЕЙ ... выполнения задания на курсовую работу была создана программа VI Function 2.0 , находящая корни алгебраического многочлена вида (1) с указываемой точностью посредством следующих методов: · метод деления отрезка пополам; · метод хорд и касательных ( ... |
|
| 2283. |
Морфологический анализ цветных (спектрозональных) изображений ... изображения несет информацию о свойствах поверхности объекта, о ее форме, а яркость в значительной степени зависит и от условий “освещения”. Поэтому на практике в задачах морфологического анализа цветных изображений сцен важное значение имеет понятие формы изображения, имеющего постоянный цвет и ... |
|
| 2284. |
Методы Хука-Дживса ... (x1,x2) = 3x12+4x1x2+5x22 , при ограничениях x1 x2 x1+x2. Текст программы
program HuDjMody; (*** Модифицированный метод Хука-Дживса ***) (*** (при наличии ограничений) ***) uses crt; label 0,1,2,3,4,5,6,7; var k,h,z,ps,bs,fb,fi :real; i,j,n,fe :integer; x,y,b,p ... |
|
| 2285. |
Множина комплексних чисел ... . Последнее равенство перепишем в следующем виде: u2 + 2uvi + v2i2 = a + bi, u2 – v2 + 2uvi = a + bi. Учитывая определение равенства комплексных чисел (см. (10)), получаем u2 – v2 = a, 2uv = b. (15) Возведем в квадрат обе части каждого из этих равенств, сложим ... |
|
| 2286. |
Многогранники ... : многогранник Г В Р тетраэдр 4-4-6 гексаэдр 6-8-12 октаэдр 8-6-12 додекаэдр 12-20-30 икосаэдр 20-12-30 И еще один вопрос возникает в связи с правильными многогранниками: можно ли ими заполнить пространство так, чтобы между ними не было просветов? Он возникает по аналогии с правильными ... |
|
| 2287. |
Минимизация функций нескольких переменных. Метод спуска ... программы Программа предназначена для нахождения точек минимума функций нескольких переменных – другими словами для минимизации этих функций. В программе реализован один из методов спуска – Градиентный метод спуска с выбором шага. Начальный шаг задается. Изменение шага осуществляется по ... |
|
| 2288. |
Минимизация функций алгебры логики ... а для КСНФ – наоборот. Диаграмма для двух логических переменных (для ДСНФ): Для трех переменных: Карты Карно используются для ручной минимизации функций алгебры логики при небольшом количестве переменных. Правило минимизации: склеиванию подвергаются 2,4,8,16, клеток и клетки, лежащие ... |
|
| 2289. |
Механические колебания в дифференциальных уравнениях ... k2, (1) Полученное уравнение определяет так называемые свободные колебания груза. Оно называется уравнением гармонического осциллятора. Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение: имеет мнимые ... |
|
| 2290. |
Методы численного моделирования МДП-структур ...
его экономичности
обуславливают
применение
регулярных
сеток, расположение
узлов в которых
подчиняется
определённым
закономерностям.
В практике
численного
моделирования
микроэлектронных
структур примеяются
как непрерывные
прямоугольные
(неравномерные),
так и треугольные
сетки (рис.2.).
Треугольная
... |
|
| 2291. |
Методы решения уравнений в странах древнего мира ... того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, • в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений. . Как составлял и решал Диофант квадратные уравнения , В “Арифметике” Диофанта нет ... |
|
| 2292. |
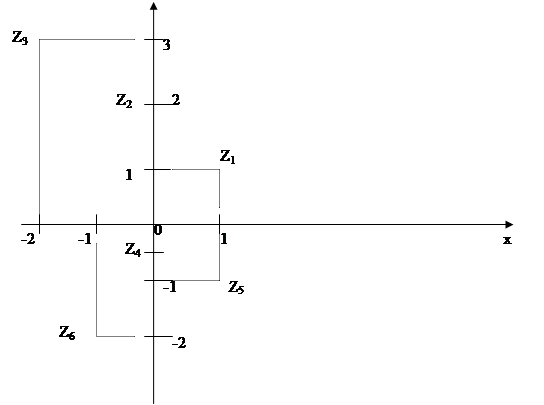
Методы решения систем линейных неравенств ... max/min целевой функции. В связи с ограниченными возможностями наглядного графического представления данный метод применяется только для систем линейных неравенств с двумя неизвестными и систем, которые могут быть приведены к данному виду. Для того чтобы наглядно продемонстрировать ... |
|
| 2293. |
Методы решения некорректно поставленных задач ... , будем называть операторным уравнением первого рода, или, короче,— уравнением первого рода. 2.1. Метод подбора решения некорректно поставленных задач 2.1.1. Широко распространенным в вычислительной практике способом приближенного решения уравнения (2; 0,1) является метод подбора ... |
|
| 2294. |
Методы обучения математике в 10 -11 класах ...
аналізаторів:
слуху, зору та
підтримання
постійного
контакту з
учнями під час
уроку.
ЛІТЕРАТУРА Махмутов М. Й. Проблемноє обучение. -М.: Педагогика, 1975. – 240 с. Методи обучения математике / Под ред. А. А. Столяра. –Минск.: Висш. шк.,1981. – 398 с. Г.П.Бевз. Методика викладання математики. 3- ... |
|
| 2295. |
Методы корреляционного и регрессионного анализа в экономических исследованиях ... потерь от брака (%); х6 – фактор, определяющий результативный признак – непроизводственные расходы (тыс./руб.). Построение регрессионной модели. Исходные данные требуется проверить на мультиколлинеарность (т.е. линейную зависимость между компонентами матрицы). ... |
|
| 2296. |
Методы и приемы решения задач ... максимальное
количество
острых углов
выпуклого
n-угольника
– три.
Доказательство
выдвинутой
гипотезы завершает
решение задачи.
4. Метод
доказательства
«от противного»
– 2
Характеристика
метода.
Имеем для
доказательства
утверждения
вида
A
B (*)
(A
– условие, B
– ... |
|
| 2297. |
Методы и алгоритмы построения элементов систем статистического моделирования ... в зависимости от класса объекта моделирования, вида оцениваемых характеристик, необходимой точности и достоверности результатов моделирования. Для метода статистического моделирования на ЭВМ характерно, что большое число операций, а соответственно большая доля машинного времени расходуются на ... |
|
| 2298. |
Методические указания по курсу Математика для студентов I курса исторического факультета ... и других периодических
изданий, а также
энциклопедические
словари.
Приложение
3.
Вопросы к зачету
по курсу “Математика”
для студентов
I курса
исторического
факультета
СГУЧасть
1. Математика. Понятие множества; элементы множества; мощность множества; отношения принадлежности и включения ... |
|
| 2299. |
Методика обучения по курсу математики за 3 года ... с тем, что математика, способная столь сильно влиять на эмоциональную сферу человека, содержит значительную эстетическую компоненту. Наконец, курс математики содержит практическую, утилитарную составляющую. Для ориентации в современном мире каждому совершенно необходим некий набор знаний и ... |
|
| 2300. |
Методика изучения числовых систем ... дроби? При этом можно рассмотреть и сокращение дроби, когда числитель и знаменатель представляют произведение. Перейдем теперь к изложению той методики преподавания умножения на дробь, которая получила в настоящее время признание в педагогической практике и в учебно-методической литературе. Можно ... |