Навигация
Физика как источник теорем дифференциального исчисления
А.В.Ястребов
В статье показано, что житейские, донаучные представления студентов о физическом мире представляет собой педагогически значимую величину, которую целесообразно использовать в процессе преподавания математики. Выявлено физическое происхождение условий некоторых математических теорем. Предложены элементы методики изложения основных теорем дифференциального исчисления, основанные на их взаимосвязи с физикой. Статья написана в рамках авторской концепции моделирования базовых свойств научных исследований в учебном процессе. 1. Об уровне физической интуиции студентов
Для определения уровня физической интуиции студентов автором был поставлен эксперимент, проводившийся 1987-88 годах на базе Ярославского государственного педагогического университета (ЯГПУ) и Ярославского государственного университета (ЯрГУ) [4, 5].
В основу эксперимента были положены следующие соображения. Во-первых, математику естественно рассматривать как составную часть естествознания. По этому поводу знаменитый математик нашего века Дж. фон Нейман пишет следующее: "Некоторые из наиболее ярких идей современной математики (я убежден, что это - ее лучшие идеи) отчетливо прослеживаются до своих истоков в естественных науках" [2]. Сужая объект рассмотрения и говоря о математическом анализе, мы можем сказать, что он был создан для описания механических движений тел. Известный российский математик А.Н.Крылов пишет: "Ньютон открыл и дал основы исчисления бесконечно малых, исходя из понятий механических и геометрических". (Цит. по книге А.Н.Колмогорова [1. С. 95].) Во-вторых, создатели математического анализа - Ньютон, Эйлер, братья Бернулли и другие - не были "чистыми" математиками, а имели серьезные труды в области механики, физики, астрономии и других наук. Естественно, что в их сознании не было перегородки, отделяющей математику от физики. Изучение движений тел давало материал для введения математических понятий, а математические теоремы позволяли описывать движения тел и находить физические законы. Преподаватель, приступающий к изложению дифференциального исчисления, может попытаться так организовать его изучение, чтобы студенты получили и усвоили информацию примерно тем же путем, каким усвоили ее создатели математического анализа.
Обращаясь к опыту детей, следует сказать, что они наблюдают движения тел с самого раннего возраста. Они легко могут сравнить скорость движения качелей в верхней и нижней точке, достаточно хорошо описывают движение поезда в момент смены направления движения и т.п. Преподаватель, приступающий к изложению дифференциального исчисления, должен уметь активизировать представления детей о физическом мире и направить их в нужное русло.
Все вышесказанное привело к той гипотезе, которая высказана в резюме в качестве утверждения. Для ее проверки был проведен эксперимент со студентами первых двух курсов упомянутых вузов. В нем участвовали 374 человека, обучающихся на разных факультетах и приобретающих разные специальности:
| ЯГПУ | ЯрГУ | Всего | ||
| Математика | Физика | Экономика | Физика | |
| 102 | 89 | 117 | 66 | 374 |
Важной характеристикой эксперимента является момент его проведения: первая неделя обучения, т.е. момент, когда математический анализ еще не развернут в сколько-нибудь стройную теорию.
Эксперимент протекал следующим образом. Аудитории объяснялось, что экспериментаторы имеют своей целью выяснить, насколько хорошо первокурсники знают школьную физику, а затем предлагалось несколько вопросов, касающихся движения тел. На первые два вопроса студенты отвечали так, как они считали нужным. Для двух других были приведены априорные ответы, из которых студенту предлагалось выбрать один. Вопрос I. Тело движется по прямой в течение некоторого отрезка времени. Сравните минимальную скорость vmin, максимальную скорость v^ и среднюю скорость vav.
Вопрос II. Тело движется по прямой в течение некоторого отрезка времени. Сравните минимальную скорость vmin, максимальную скорость v^ и мгновенную скорость v(t) в произвольный момент времени t.
Вопрос III. Тело движется по прямой в течение некоторого отрезка времени. Справедливо ли следующее утверждение: существует момент времени, такой, что скорость тела в этот момент равна средней скорости тела? Ответы: 1) Да. 2) Нет. 3) Не знаю.
Вопрос IV. Тело движется по прямой в течение некоторого отрезка времени, причем в конечный момент времени оно возвращается в исходное положение. Какова скорость тела в момент наибольшего удаления?
Ответы: 1) Больше нуля. 2) Меньше нуля. 3) Равна нулю. 4) Не знаю. Результаты ответов на первые два вопроса содержатся в следующей таблице:
| "Почти правильный" ответ | Правильный ответ | Всего | |
| Вопрос I | 13% | 70% | 83% |
| Вопрос II | 39% | 35% | 74% |
Правильные ответы на вопросы I и II представляют собой неравенства vmin ≤ vav ≤ vmax и vmin ≤ v(t - vmax соответственно. Их дают 70% и 35% респондентов (третий столбец таблицы). В то же время существуют ответы на эти вопросы, которые, будучи формально неверными, тем не менее свидетельствуют о достаточной интуиции. Имеются в виду неравенства vmin < vav < v^ и vmin < v(t) < vmax, которые получены из правильных ответов заменой знака нестрогого неравенства ≤ на знак строгого неравенства <. Они названы нами "почти правильными", т.к. не учитывают всего лишь один частный случай -случай прямолинейного равномерного движения для вопроса I и случай совпадения момента времени t с моментом экстремальной скорости для вопроса II. Результаты показывают, что существует достаточно большая группа студентов, которые правильно решают физическую задачу.
Сформулированные вопросы выполняют в данном эксперименте различные функции. Первые два играют вспомогательную роль. Они восстанавливают в аудитории атмосферу школьного урока физики, заставляют респондентов мыслить в уже освоенных категориях: скорость, средняя скорость, мгновенная скорость и т.д. На два других ложится основная смысловая нагрузка, т.к. именно они вскрывают уровень физической интуиции студентов.
Результаты эксперимента приведены в нижеследующей таблице. Полученные данные выражены в абсолютных единицах, а для правильных ответов также и в процентах, которые округлены до целых. Наиболее важные результаты выделены жирным шрифтом.
| ЯГПУ | ЯрГУ | ВСЕГО | ||||
| Математика | Физика | Экономика | Физика | |||
| Число респондентов | 102 | 89 | 117 | 66 | 374 | |
| о о & о PQ | Да | 58 (57%) | 56 (63%) | 106 (90%) | 60 (91%) | 280 (75%) |
| Нет | 34 | 22 | 8 | 4 | 68 | |
| Не знаю | 10 | 11 | 3 | 2 | 26 | |
| v = 0 | 82 (80%) | 64 (72%) | 88 (75%) | 54 (82%) | 288 (77%) | |
| > о о PQ | v>0 | 8 | 16 | 16 | 4 | 44 |
| v<0 | 6 | 5 | 6 | 3 | 20 | |
| Не знаю | 6 | 4 | 7 | 5 | 22 | |
| на оба вопроса | 50 (49%) | 38 (43%) | 76 (65%) | 50 (76%) | 214 (57%) | |
| Верно | по крайней мере на один вопрос | 90 (88%) | 84 (94%) | 115 (98%) | 64 (97%) | 353 (94%) |
Разъясним математическую и физическую сущности вопросов и дадим комментарии к эксперименту. Пусть [a, b] - промежуток времени, в течение которого движется тело, s(t) - закон движения тела, а v(t) - его мгновенная скорость. Утвердительный (и верный) ответ на вопрос III означает, что существует момент времени t0, такой, что
![]()
(1)
Скорость является производной от пути по времени:
![]()
Средняя скорость по
определению равна
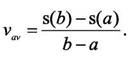
Подставляя эти выражения в равенство (1), полу-
чим формулу
![]()
(2)
которая представляет собой формулу Лагранжа.
Результаты эксперимента показывают, что на интуитивном, физическом уровне 75% респондентов могут самостоятельно сформулировать теорему Лагранжа, являющуюся одной из основных теорем дифференциального исчисления (последний столбец таблицы, строка с ответом "да").
Для выяснения сущности вопроса IV воспользуемся теми же обозначениями. Верный ответ состоит в том, что скорость тела в момент наибольшего удаления равна нулю. Если t0 - момент наибольшего удаления, то v(t0) = 0, или s'(O = 0. Получается, что если s(b) = s(a) (тело возвращается в исходное положение), то существует момент времени t0, такой, что s′(t0) = 0. Это утверждение является теоремой Ролля. Результаты эксперимента показывают, что на интуитивном, физическом уровне 77% респондентов могут самостоятельно сформулировать теорему Ролля, являющуюся одной из основных теорем дифференциального исчисления (последний столбец таблицы, строка с ответом v = 0).
Особого внимания заслуживают две последние клетки последнего столбца таблицы. Дело в том, что теоремы Ролля и Лагранжа занимают центральное место в курсе дифференциального исчисления, поскольку именно из них выводятся основные утверждения, применяемые при исследовании функций и построении их графиков: критерий постоянства функции, достаточное условие монотонности, достаточное условие экстремума. Тот факт, что 57% респондентов в состоянии самостоятельно сформулировать на интуитивном уровне две серьезные математические теоремы, говорит о достаточно хорошей физической интуиции студентов и о том, что эту интуицию следует активно использовать в преподавании дифференциального исчисления. Теоремы Ролля и Лагранжа выводятся чисто логически одна из другой, поэтому оказывается весьма важным тот факт, что 94% респондентов могут на интуитивном уровне самостоятельно сформулировать по крайней мере одну из них. Он говорит о том, что стимулирование физической интуиции при изучении математики встретит достаточно адекватную реакцию практически всей студенческой аудитории.
Данные эксперимента говорят о том, что нет прямой зависимости между ориентацией на физико-математические науки и физической интуицией в исследуемой области и на исследуемом уровне. Так, данные для экономистов (специальность "бухгалтерский учет") показывают, что они сопоставимы с результатами математиков и даже физиков (см. строки с правильными ответами и две последние строки).
Интересно, что респонденты не связывали задаваемые им физические вопросы с математическим материалом, о чем свидетельствовали собеседования, проводимые с аудитори-ей.
Достоверность полученных результатов оценивалась с помощью критерия "хи-квадрат". Подсчет показал следующее: вероятность того, что данные цифры получены в результате случайного (равновероятного) выбора одного из возможных априорных ответов, много меньше 0,001.
Итак, данные эксперимента говорят о том, что физическая интуиция студентов представляет собой значимую величину, активное использование которой в процессе преподавания является вполне естественным. Ниже мы покажем, что ее использование не только естественно, но и весьма эффективно.
Похожие работы
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
... анализа генезиса теоретических схем технических наук в процессе модификации теоретических схем соответствующей базовой физической теории (электродинамики). Экспериментальное доказательство Герцем теории Максвелла и его технические следствия Заимствованная из механики и акустики теоретическая схема естественного волнового процесса позволяла транслировать для случая электромагнитных волн и ...
... формулы Ньютона — Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научиться находить первообразные многих функций, дать логические основы нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано. Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summa). Само слово ...
... коэффициенты an (x1), bn (x1), an (x2), bn (x2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а2. Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. §3.1. Дифракция излучения на сферической частице. Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в ...



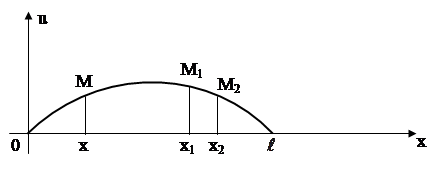
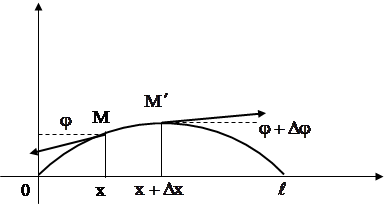
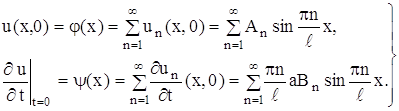

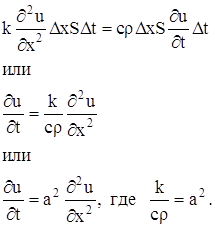
0 комментариев