Навигация
Теоретические основы таблично алгоритмического метода
4. Теоретические основы таблично алгоритмического метода
В основе методов, основанных на применении таблиц, лежит разбиение интервала аппроксимации на промежутки h (шаг таблицы), длина которых выбирается пропорционально основанию используемой системы счисления. Значения функций, подлежащей реализации, предварительно вычисляются для концов промежутков и заносятся в таблицу, роль которой выполняет ПЗУ. Однако данный подход кроме значительной емкости ПЗУ трудно реализовать вследствие значительности объема предварительных вычислений.
В связи с этим широкое применение в настоящее время нашли таблично алгоритмические методы вычислений, сочетающие поиск по таблице с грубым значением аргумента и введением поправок на точное значение. При определении поправки, характерной для данных методов, может использоваться следующая формула:
![]() F(x)=F(xs+D xn-s)= F(xs)+Ф(D xn-s, xs),
F(x)=F(xs+D xn-s)= F(xs)+Ф(D xn-s, xs),
где xs – s-разрядный код старшей части аргумента Х,
0£D xn-s<2-s – (n-s)-разрядный код младшей части аргумента Х,
F(xs) – табличное значение функции F(x) для точки xs,
Ф(D xn-s, xs) – поправка.
В данном случае величина s, являясь разрядностью аргумента xs , задает значение шага таблицы h=2-s, а также количество табличных значений функции F(xs), равное 2s. Поправки Ф(D xn-s, xs) определяются в процессе работы микроЭВМ. Их находят с помощью различных методов, к которым, прежде всего, относятся: разложение в степенные ряды, цепные дроби, дробно рациональные приближения, интерполирование, численное интегрирование, итерационные процессы.
Принципы использования частных методов вычисления поправок, основанных на применении известных тождеств для каждой конкретной элементарной функции. Этот подход характеризуется точностью базовой формулы, зависимостью поправки для большинства элементарных функций только от младшей части аргумента. Чаще всего данный метод является нерациональным из-за значительного числа дополнительных операций.
Формула для вычисления значения F(x) на интервале (xs, xs+h) с использованием ряда Тейлора имеет следующий вид:
F(x)= F(xs) + ![]() D xn-s/k!)*F(k)( xs),
D xn-s/k!)*F(k)( xs),
где m – количество членов ряда , D xn-s=x - xs,
F(k)( xs) – значение k-ой производной функции F(x) в точке xs.
Методическая погрешность приведенного алгоритма можно оценить по формуле:
eм£((D xn-s)m+1/(m+1)!)*F(m+1)max
где F(m+1)max – максимальное значение (m+1)-ой производной функции F(x) на интервале (xs, xs+h).
Формула для вычисления значения F(x) на интервале (xs, xs+h) с помощью линейной интерполяции имеет следующий вид:
F(x)= F(xs) + (D xn-s/h)*(F(xs, xs+h) - F(xs))
Методическая погрешность приведенного алгоритма можно оценить по формуле:
eм£(D xn-s(D xn-s – h)/2)*F(2)max
Формулы для вычисления погрешностей:
- полной e = Fэт(х) - Fm(xm)/Mf
- методической eм £ ((D xn-s)m-1/(m+1)!)*F(m+1)max
- вычислительной eв = Fэт* - Fm(xm)/Mf
5. Расчет параметров алгоритма
Одной из задач проектирования алгоритмов таблично алгоритмических методов является удовлетворение требований по времени вычисления элементарной функции в микроЭВМ и точности вычислений, которая обусловлена заданной разрядностью представления аргумента.
Требование по времени tдоп можно выполнить, ограничивая такие параметры численных методов как число членов ряда, полинома, цепной дроби, шагов итераций и т. п. При этом учитывается время выполнения в микро-ЭВМ арифметических, логических и других используемых операций.
Необходимая точность вычислений обеспечивается путем выполнения баланса методической и вычислительной погрешностей алгоритма в виде условия eм = eв где в качестве eв выступает ее минимальное значение 2-(n+1).
В случае разложения в ряд Тейлора баланс погрешностей имеет вид:
((D xn-s)m+1/(m+1)!)*|F(m+1)max| = 2-(n+1)
Учитывая что D xn-s = 2-s имеем:
S ³ (n + 1 - log2((m+1)!)/|F(m+1)max|)/(m+1)
Для большинства элементарных функций зависимость s(m) хорошо аппроксимируется соотношением:
S ³ (n + 1 – 2m*log2e)/(m+1)
Следовательно, по известной разрядности аргумента n и количеству членов ряда m можно оценить минимальную разрядность s старшей части аргумента X, обеспечивающую требуемый баланс методической и вычислительной погрешностей.
В случае использования кусочно-линейной интерполяции баланс погрешностей имеет вид:
(D xn-s|D xn-s – h|/2)*|F(2)max| = 2-(n+1)
Поскольку h=2-s, то левая часть этого неравенства достигает максимального абсолютного значения при D xn-s = 2-(s+1).Тогда
2-2s *|F(2)max|/8 = 2-(n+1)
Отсюда окончательно получаем:
S ³ (n + log2|F(2)max| - 2)/2
Величина s является тем параметром, который обеспечивает баланс методической и вычислительной погрешностей, а также определяет не только разрядность старшей части аргумента Х, но и значение шага таблицы h = 2-s и количество табличных значений функции F(xs) равное 2s.
Похожие работы
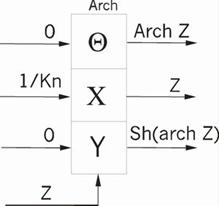
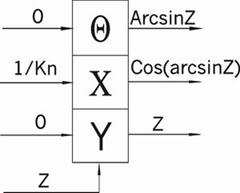
ть специализированный математический процессор для вычисления элементарных функций arcSin(Z) и arCth(Z). Эти функции можно реализовать методом Волдера «Цифра за цифрой», метод Меджита и др. Оба эти метода основаны на ряде итерационных формул, которые приведены в таблице 1.1. Основное их различие заключается в том, что в методе Меджита на первом этапе сразу рассчитываются все направляющие ...
... к гамма-функции с положительным целым параметром, гамма-функции с положительным параметром, гамма-функции для множества точек. Созданная функциональная модель реализации основных способов вычисления гамма функции и ее программная реализация могут служить органической частью решения более сложных задач. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы 1. Бронштейн, И.Н. Справочник по ...
... что знак конъюнкции, как правило, опускается). Предыдущая формула приводит к важной теореме. Теорема. Всякая логическая функция может быть представлена булевой формулой, то есть как суперпозиция конъюнкции, дизъюнкции и отрицания. Действительно, для всякой функции, кроме константы 0, таким представлением может служить её СДНФ. Константу 0 можно представить булевой формулой Ø xx. А почему ...
... , которые содержат неизвестную функцию, её производные и аргументы. Обыкновенным называется дифференциальное уравнение, в котором неизвестная функция является функцией одной переменной. Если неизвестная функция является функцией многих переменных, то соответствующее уравнение называется дифференциальным уравнением в частных производных. Порядком дифференциального уравнения называется наивысший ...
0 комментариев