Навигация
Геометрическая интерпретация ЗЛП и графический метод решения (при двух неизвестных)
5. Геометрическая интерпретация ЗЛП и графический метод решения (при двух неизвестных)
![]() Система ограничений ЗЛП геометрически представляет собой многоугольник или многоугольную область как пересечение полуплоскостей - геометрических образов неравенств системы. Целевая функция f = c1x1 + c2x2 геометрически изображает семейство параллельных прямых, перпендикулярных вектору n (с1,с2).
Система ограничений ЗЛП геометрически представляет собой многоугольник или многоугольную область как пересечение полуплоскостей - геометрических образов неравенств системы. Целевая функция f = c1x1 + c2x2 геометрически изображает семейство параллельных прямых, перпендикулярных вектору n (с1,с2).
![]() Теорема. При перемещении прямой целевой функции направлении вектора n значения целевой функции возрастают, в противоположном направлении - убывают.
Теорема. При перемещении прямой целевой функции направлении вектора n значения целевой функции возрастают, в противоположном направлении - убывают.
На этих утверждениях основан графический метод решения ЗЛП.
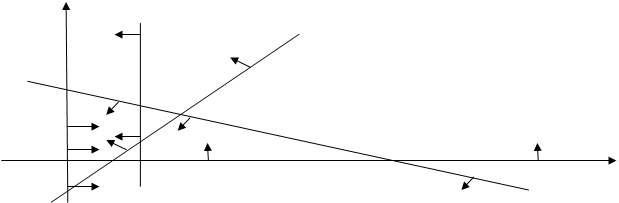
Алгоритм графического метода решения ЗЛП.
· В системе координат построить прямые по уравнениям, соответствующим каждому неравенству системы ограничений;
· найти полуплоскости решения каждого неравенства системы (обозначить стрелками);
· найти многоугольник (многоугольную область) решений системы ограничений как пересечение полуплоскостей;
· ![]() построить вектор n (с1,с2) по коэффициентам целевой функции f = c1x1 + c2x2;
построить вектор n (с1,с2) по коэффициентам целевой функции f = c1x1 + c2x2;
· в семействе параллельных прямых целевой функции выделить одну, например, через начало координат;
· перемещать прямую целевой функции параллельно самой себе по области решения, достигая max f при движении вектора n и min f при движении в противоположном направлении.
· найти координаты точек max и min по чертежу и вычислить значения функции в этих точках (ответы).
Постановка транспортной задачи.
Приведем экономическую формулировку транспортной задачи по критерию стоимости:
Однородный груз, имеющийся в m пунктах отправления (производства) А1, А2, ..., Аm соответственно в количествах а1, а2, ..., аmединиц, требуется доставить в каждый из n пунктов назначения (потребления) В1, В2, ..., Вn соответственно в количествах b1, b2, ..., bn единиц. Стоимость перевозки (тариф) единицы продукта из Ai в Bj известна для всех маршрутов AiBj и равна Cij (i=1,m; j=1,n). Требуется составить такой план перевозок, при котором весь груз из пунктов отправления вывозиться и запросы всех пунктов потребления удовлетворяются (закрытая модель), а суммарные транспортные расходы минимальны.
Условия задачи удобно располагать в таблицу, вписывая в клетки количество перевозимого груза из Ai в Bjгруза Xij > 0, а в маленькие клетки - соответствующие тарифы Cij:
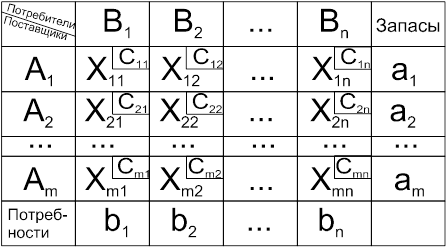
Математическая модель транспортной задачи.
Из предыдущей таблицы легко усматривается и составляется математическая модель транспортной задачи для закрытой модели
![]()
Число r = m + n - 1, равное рангу системы (1), называется рангом транспортной задачи. Если число заполненных клеток (Xij <>0) в таблице равно r, то план называется невырожденным, а если это число меньше r, то план вырожденный - в этом случае в некоторые клетки вписывается столько нулей (условно заполненные клетки), чтобы общее число заполненных клеток было равно r.
Случай открытой модели легко сводится к закрытой модели путем введения фиктивного потребителя Bn+1 c потребностью bn+1=Σai-Σbj, либо - фиктивного поставщика Аm+1 c запасом am+1=Σbj-Σai ; при этом тарифы фиктивных участников принимаются равными 0.
Способы составления 1-таблицы (опорного плана).
Способ северо-западного угла (диагональный). Сущность способа заключается в том, что на каждом шаге заполняется левая верхняя клетка (северо-западная) оставшейся части таблицы, причем максимально возможным числом: либо полностью вывозиться груз из Аi, либо полностью удовлетворяется потребность Bj. Процедура продолжается до тех пор, пока на каком-то шаге не исчерпаются запасы ai и не удовлетворяются потребности bj. В заключение проверяют, что найденные компоненты плана Xij удовлетворяют горизонтальным и вертикальным уравнениям и что выполняется условие невырожденности плана.
Способ наименьшего тарифа. Сущность способа в том, что на каждом шаге заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф; в случае наличия нескольких таких равных тарифов заполняется любая из них. В остальном действуют аналогично предыдущему способу.
Метод потенциалов решения транспортной задачи.
Определение: потенциалами решения называются числа iAi, jBj, удовлетворяющие условию i+j=Cij (*) для всех заполненных клеток (i,j).
Соотношения (*) определяют систему из m+n-1 линейных уравнений с m+n неизвестными, имеющую бесчисленное множество решений; для ее определенности одному неизвестному придают любое число (обычно 1=0), тогда все остальные неизвестные определяются однозначно.
Критерий оптимальности. Если известны потенциалы решения X0 транспортной задачи и для всех незаполненных клеток выполняются условияi+j Ci j, то X0 является оптимальным планом транспортной задачи.
Если план не оптимален, то необходимо перейти к следующему плану (таблице) так, чтобы транспортные расходы не увеличились.
Определение: циклом пересчета таблицы называется последовательность клеток, удовлетворяющая условиям:
· одна клетка пустая, все остальные занятые;
· любые две соседние клетки находятся в одной строке или в одном столбце;
· никакие 3 соседние клетки не могут быть в одной строке или в одном столбце .
Пустой клетке присваивают знак “ + ”, остальным - поочередно знаки “ - ” и “ + ”.
Для перераспределения плана перевозок с помощью цикла перерасчета сначала находят незаполненную клетку (r, s), в которой r+sCrs, и строят соответствующий цикл; затем в минусовых клетках находят число X=min{Xij}.Далее составляют новую таблицу по следующему правилу:
· в плюсовые клетки добавляем X;
· из минусовых клеток отнимаем Х;
· все остальные клетки вне цикла остаются без изменения.
Получим новую таблицу, дающее новое решение X, такое, что f(X1) f(X0); оно снова проверяется на оптимальность через конечное число шагов обязательно найдем оптимальный план транспортной задачи, ибо он всегда существует.
Алгоритм метода потенциалов.
· проверяем тип модели транспортной задачи и в случае открытой модели сводим ее к закрытой;
· находим опорный план перевозок путем составления 1-й таблицы одним из способов - северо-западного угла или наименьшего тарифа;
· проверяем план (таблицу) на удовлетворение системе уравнений и на не вырожденность; в случае вырождения плана добавляем условно заполненные клетки с помощью “ 0 ”;
· проверяем опорный план на оптимальность, для чего:
· а) составляем систему уравнений потенциалов по заполненным клеткам;
· б) находим одно из ее решений при 1=0;
· в) находим суммыi+j=Cij (“косвенные тарифы”) для всех пустых клеток;
· г) сравниваем косвенные тарифы с истинными: если косвенные тарифы не превосходят соответствующих истинных(Cij Cij) во всех пустых клетках, то план оптимален (критерий оптимальности). Решение закончено: ответ дается в виде плана перевозок последней таблицы и значения min f.
Если критерий оптимальности не выполняется, то переходим к следующему шагу.
Для перехода к следующей таблице (плану):
· а) выбираем одну из пустых клеток, где косвенный тариф больше истинного (Cij=i+j > Cij );
· б) составляем цикл пересчета для этой клетки и расставляем знаки “ + ”, “ - ” в вершинах цикла путем их чередования, приписывая пустой клетке “ + ”;
· в) находим число перерасчета по циклу: число X=min{Xij}, где Xij- числа в заполненных клетках со знаком “ - ”;
· г) составляем новую таблицу, добавляя X в плюсовые клетки и отнимая X из минусовых клеток цикла
· См. п. 3 и т.д.
Через конечное число шагов (циклов) обязательно приходим к ответу, ибо транспортная задача всегда имеет решение.
Похожие работы
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...
... рулонов, при котором все поступающие специальные заявки будут выполнены при минимальных затратах бумаги. Графический метод решения задач линейного программирования 1. Область решений линейных неравенств. Пусть задано линейное неравенство с двумя переменными и (1) Если величины и рассматривать как координаты точки плоскости, то совокупность точек ...
... вторым способом, тогда мы получим 600 заготовок первого вида, 200 – второго, 400 – третьего, 400 – четвёртого, при минимальных отходах, равных 56 м2.Экономическая сущность и математическое моделирование транспортных задач.Известны: пункты производства (А1, А2 … Ai … Аm); m – пунктов, производящих конкретную продукцию; аi – мощность i-поставщика (сколько необходимо реализовать продукции, т. е. ...
... 175 * 8 + 25 * 4 = 8085. По сравнению с исходным решением, транспортные расходы уменьшились на 175 усл.ед. (8260 – 8085 = 175). Задачи 41–50. Составить экономико-математическую модель. Найти решение задачи линейного программирования при помощи средств Excel на ПК. 48. В суточном рационе кормления крупного рогатого скота должно быть не менее 20 кормовых единиц, не менее 2000 г белков и не ...

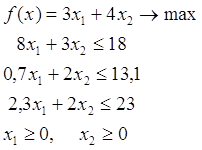

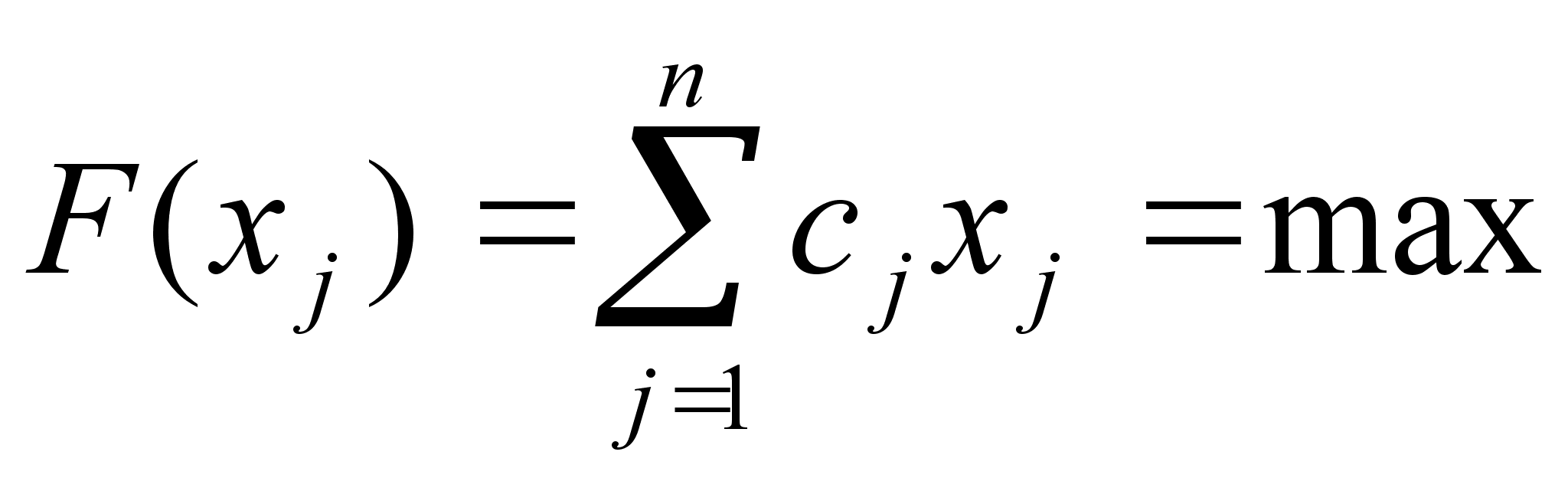
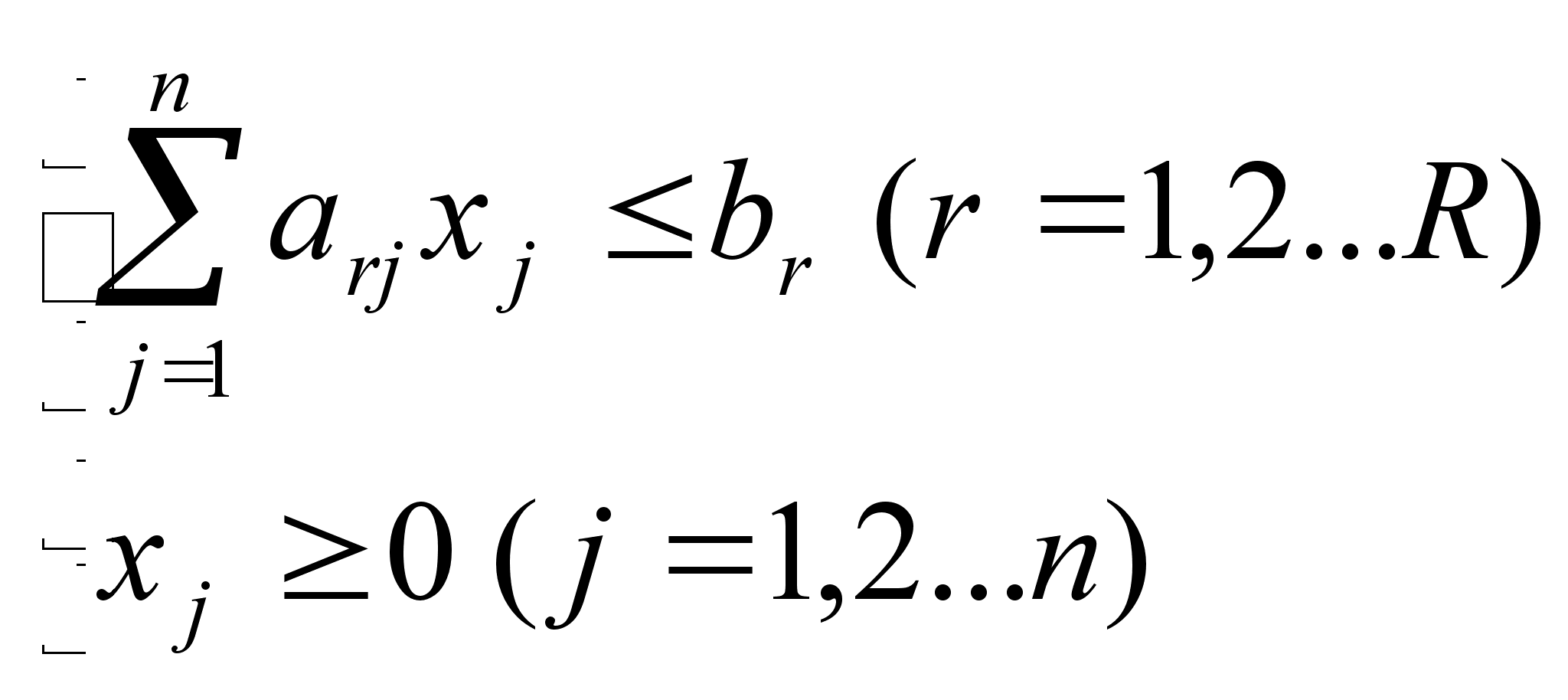
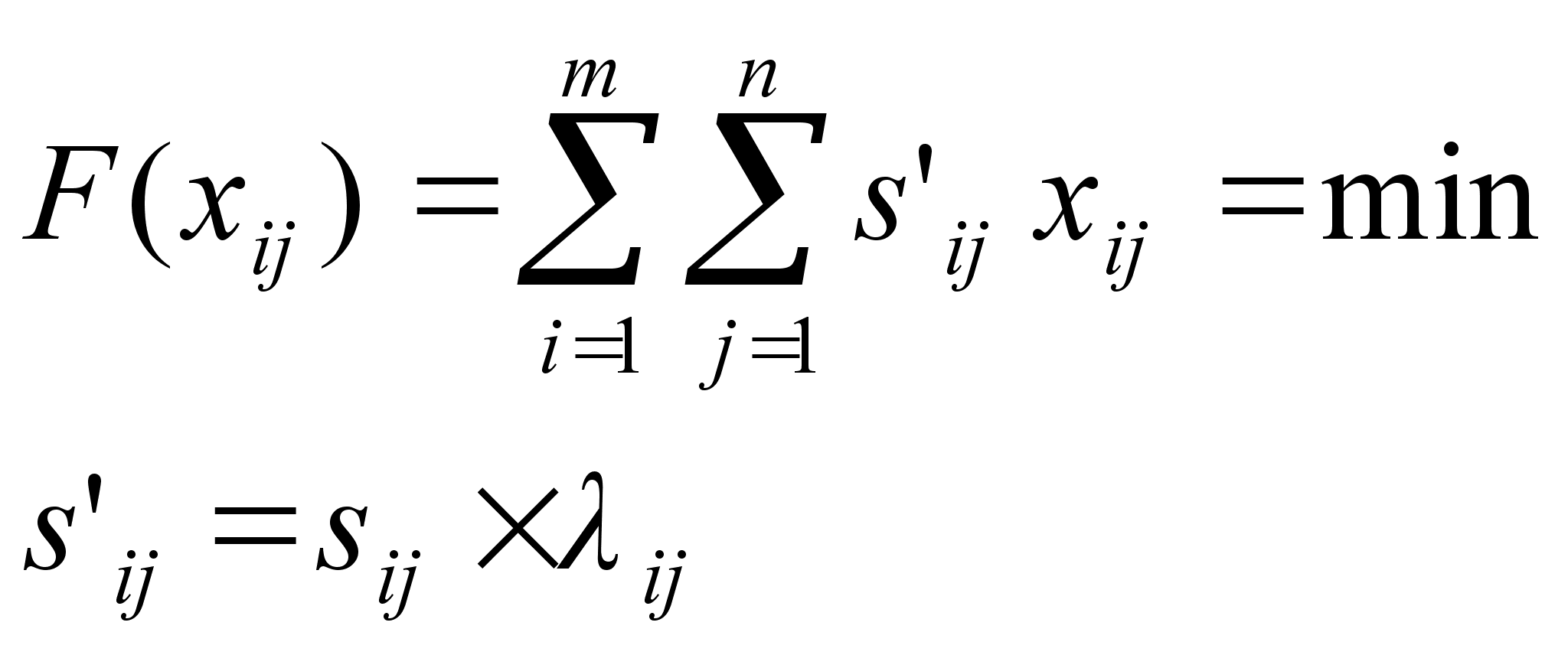
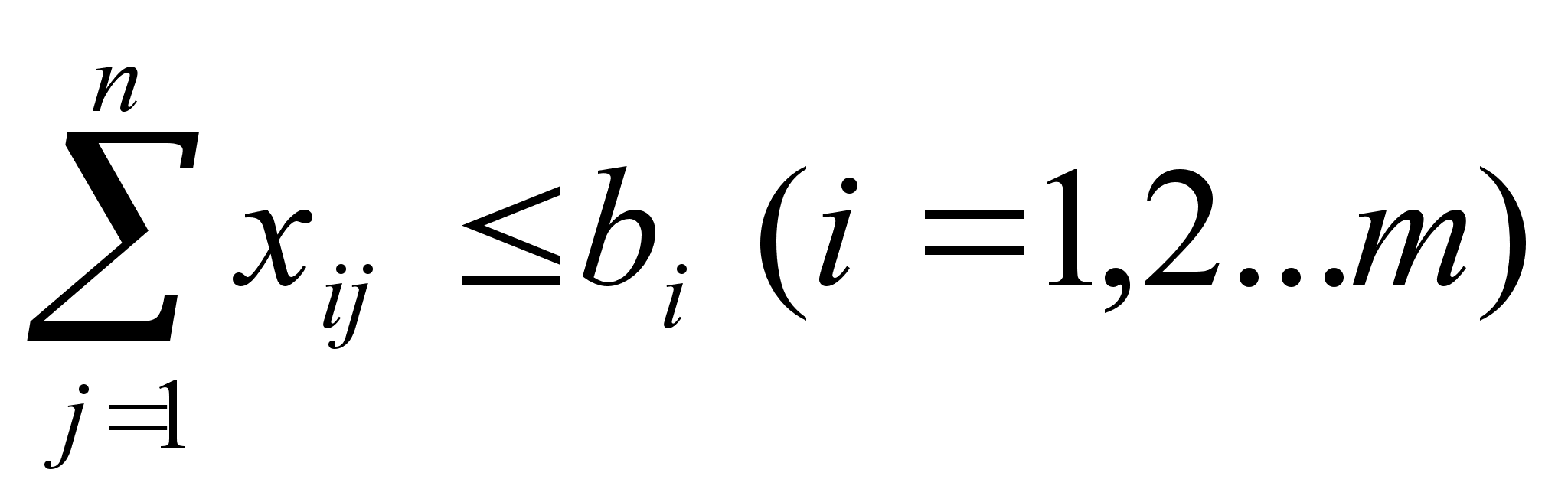
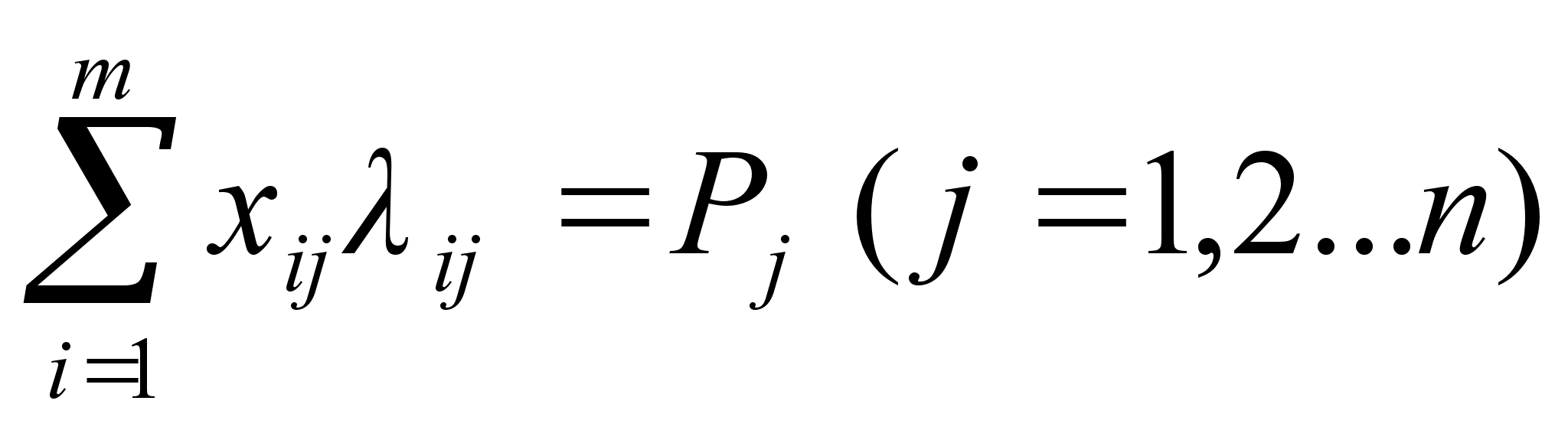
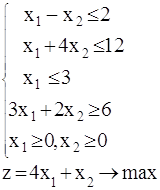

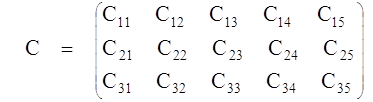
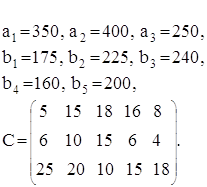
0 комментариев