Навигация
Математическое программирование
Общая задача линейного программирования (ЗЛП):
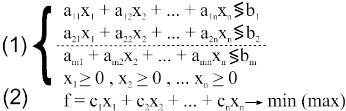
Здесь (1) называется системой ограничений , ее матрица имеет ранг r £ n, (2) - функцией цели (целевой функцией). Неотрицательное решение (х10, x20, ... , xn0) системы (1) называется допустимым решением (планом) ЗЛП. Допустимое решение называется оптимальным, если оно обращает целевую функцию (2) в min или max (оптимум).
Симплексная форма ЗЛП. Для решения ЗЛП симплекс - методом необходимо ее привести к определенной (симплексной) форме:
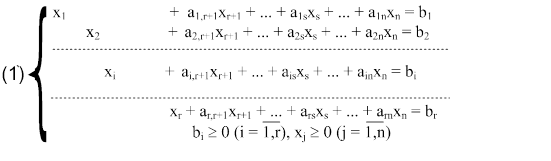 (2`) f+cr+1xr+1 + ... + csxs + ... + cnxn = b0 ® min
(2`) f+cr+1xr+1 + ... + csxs + ... + cnxn = b0 ® min
Здесь считаем r < n (система имеет бесчисленное множество решений), случай r = n неинтересен: в этом случае система имеет единственное решение и если оно допустимое, то автоматически становится оптимальным.
В системе (1`) неизвестные х1, х2, ... , хr называются базисными (каждое из них входит в одно и только одно уравнение с коэффициентом +1), остальные хr+1, ... , xn - свободными. Допустимое решение (1`) называется базисным (опорным планом), если все свободные неизвестные равны 0, а соответствующее ему значение целевой функции f(x10, ... , xr0,0, ... ,0) называется базисным.
В силу важности особенностей симплексной формы выразим их и словами:
а) система (1`) удовлетворяет условиям :
все ограничения - в виде уравнений;
все свободные члены неотрицательны, т.е. bi ³ 0;
имеет базисные неизвестные;
б) целевая функция (2`) удовлетворяет условиям :
содержит только свободные неизвестные;
все члены перенесены влево, кроме свободного члена b0;
обязательна минимизация (случай max сводится к min по формуле max f = - min(-f)).
Матричная форма симплекс-метода. Симплексной форме ЗЛП соответствует симплекс - матрица :
Заметим, что каждому базису (системе базисных неизвестных ) соответствует своя симплекс - матрица , базисное решение х = (b1,b2, ... ,br, 0, ... ,0) и базисное значение целевой функции f(b1,b2, ... ,br, 0, ... ,0) = b0 (см. Последний столбец !).
Критерий оптимальности плана . Если в последней (целевой) строке симплекс-матрицы все элементы неположительны, без учета последнего b0, то соответствующий этой матрице план оптимален,
![]() т.е. сj £ 0 (j = r+1, n) => min f (b1, ... ,b2,0, ... ,0) = b0.
т.е. сj £ 0 (j = r+1, n) => min f (b1, ... ,b2,0, ... ,0) = b0.
![]() Критерий отсутствия оптимальности. Если в симплекс-матрице имеется столбец (S-й), в котором последний элемент сs > 0, a все остальные элементы неположительны, то ЗЛП не имеет оптимального плана, т.е. сs > 0, ais £ 0 ( i= 1,r ) => min f = -¥.
Критерий отсутствия оптимальности. Если в симплекс-матрице имеется столбец (S-й), в котором последний элемент сs > 0, a все остальные элементы неположительны, то ЗЛП не имеет оптимального плана, т.е. сs > 0, ais £ 0 ( i= 1,r ) => min f = -¥.
Если в симплекс-матрице не выполняются оба критерия, то в поисках оптимума надо переходить к следующей матрице с помощью некоторого элемента ais > 0 и следующих преобразований (симплексных):
все элементы i-й строки делим на элемент a+is;
все элементы S-го столбца, кроме ais=1, заменяем нулями;
все остальные элементы матрицы преобразуем по правилу прямоугольника, что схематично показано на фрагменте матрицы и дано в формулах:
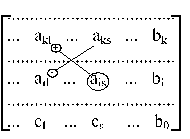
akl` = akbais - ailaks = akl - ailaks;
ais ais
bk` = bkais - biaks; cl` = clais - csail
ais ais
Определение. Элемент ais+ называется разрешающим, если преобразование матрицы с его помощью обеспечивает уменьшение (невозрастание) значения, целевой функции; строка и столбец, на пересечении которых находится разрешающий элемент, также называются разрешающими.
Критерий выбора разрешающего элемента. Если элемент ais+удовлетворяет условию
bi = min bk
ais0 aks0+
где s0 - номер выбранного разрешающего столбца, то он является разрешающим.
Алгоритм симплекс-метода (по минимизации).
систему ограничений и целевую функцию ЗЛП приводим к симплексной форме;
составим симплекс-матрицу из коэффициентов системы и целевой функции в симплексной форме;
проверка матрицы на выполнение критерия оптимальности; если он выполняется, то решение закончено;
при невыполнении критерия оптимальности проверяем выполнение критерия отсутствия оптимальности; в случае выполнения последнего решение закончено - нет оптимального плана;
в случае невыполнения обоих критериев находим разрешающий элемент для перехода к следующей матрице, для чего :
а) выбираем разрешающий столбец по наибольшему из положи тельных элементов целевой строки;
б) выбираем разрешающую строку по критерию выбора разрешающего элемента; на их пересечении находится разрешающий элемент;
c помощью разрешающего элемента и симплекс-преобразований переходим к следующей матрице;
вновь полученную симплекс-матрицу проверяем описанным выше способом (см. п. 3)
Через конечное число шагов, как правило получаем оптимальный план ЗЛП или его отсутствие
Замечания.
Если в разрешающей строке (столбце) имеется нуль, то в соответствующем ему столбце (строке) элементы остаются без изменения при симплекс-преобразованиях.
· преобразования - вычисления удобно начинать с целевой строки; если при этом окажется, что выполняется критерий оптимальности, то можно ограничиться вычислением элементов последнего столбца.
· при переходе от одной матрицы к другой свободные члены уравнений остаются неотрицательными; появление отрицательного члена сигнализирует о допущенной ошибке в предыдущих вычислениях.
· правильность полученного ответа - оптимального плана - проверяется путем подстановки значений базисных неизвестных в целевую функцию; ответы должны совпасть.
Похожие работы
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...
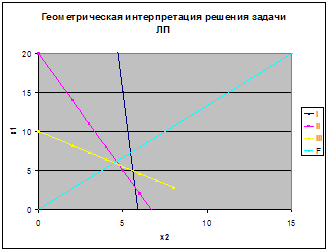
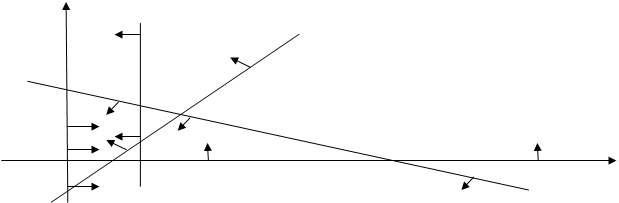
... рулонов, при котором все поступающие специальные заявки будут выполнены при минимальных затратах бумаги. Графический метод решения задач линейного программирования 1. Область решений линейных неравенств. Пусть задано линейное неравенство с двумя переменными и (1) Если величины и рассматривать как координаты точки плоскости, то совокупность точек ...
... вторым способом, тогда мы получим 600 заготовок первого вида, 200 – второго, 400 – третьего, 400 – четвёртого, при минимальных отходах, равных 56 м2.Экономическая сущность и математическое моделирование транспортных задач.Известны: пункты производства (А1, А2 … Ai … Аm); m – пунктов, производящих конкретную продукцию; аi – мощность i-поставщика (сколько необходимо реализовать продукции, т. е. ...
... 175 * 8 + 25 * 4 = 8085. По сравнению с исходным решением, транспортные расходы уменьшились на 175 усл.ед. (8260 – 8085 = 175). Задачи 41–50. Составить экономико-математическую модель. Найти решение задачи линейного программирования при помощи средств Excel на ПК. 48. В суточном рационе кормления крупного рогатого скота должно быть не менее 20 кормовых единиц, не менее 2000 г белков и не ...


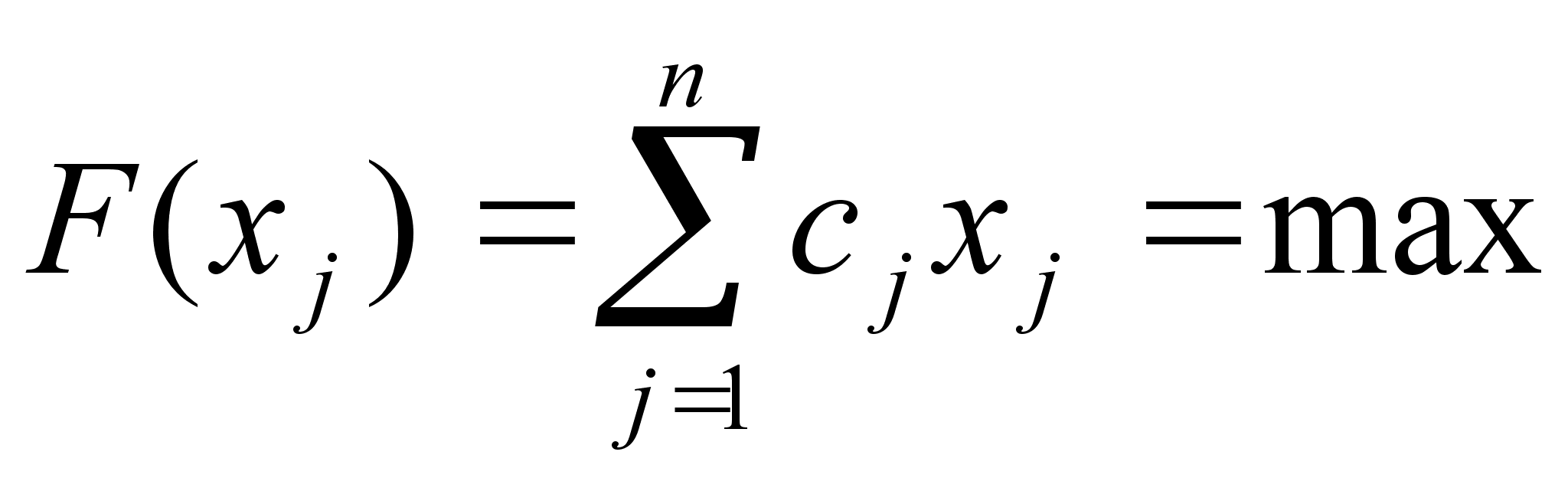
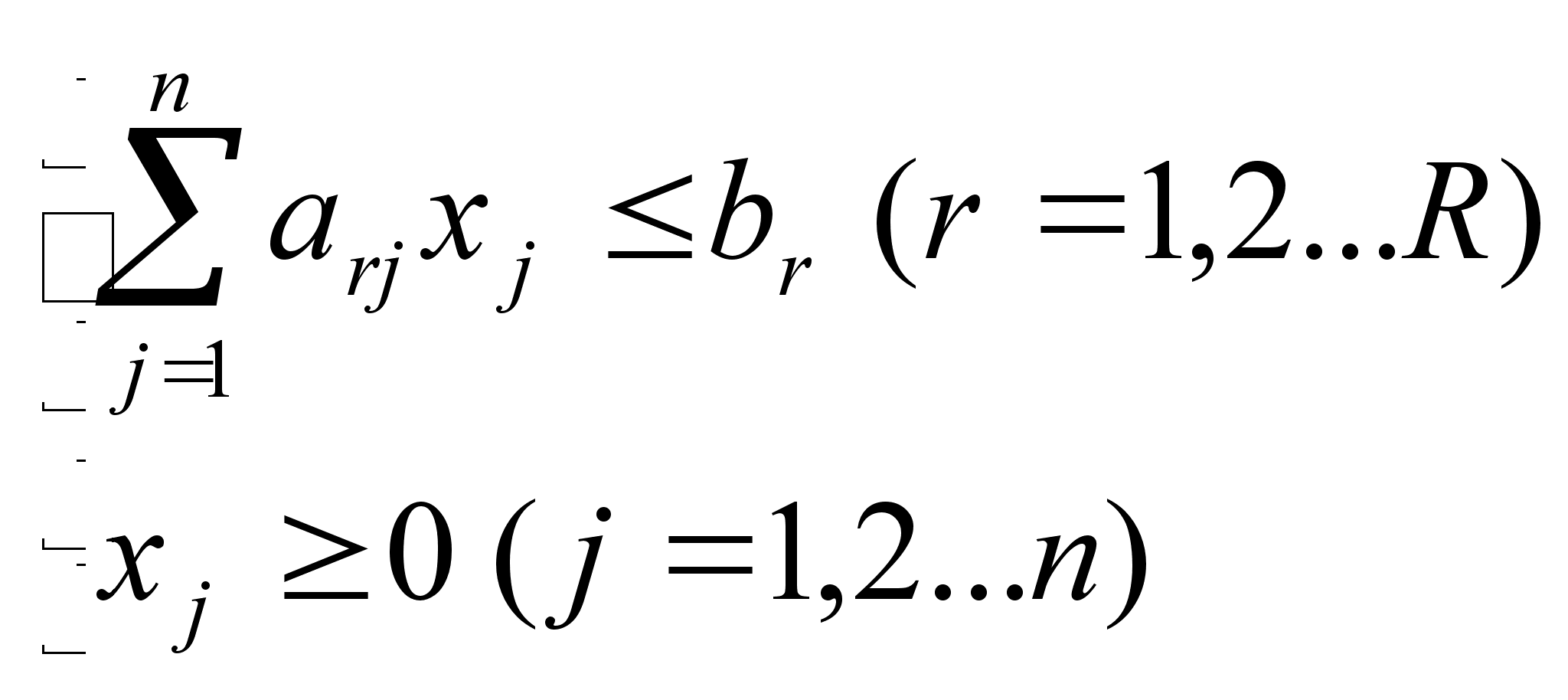
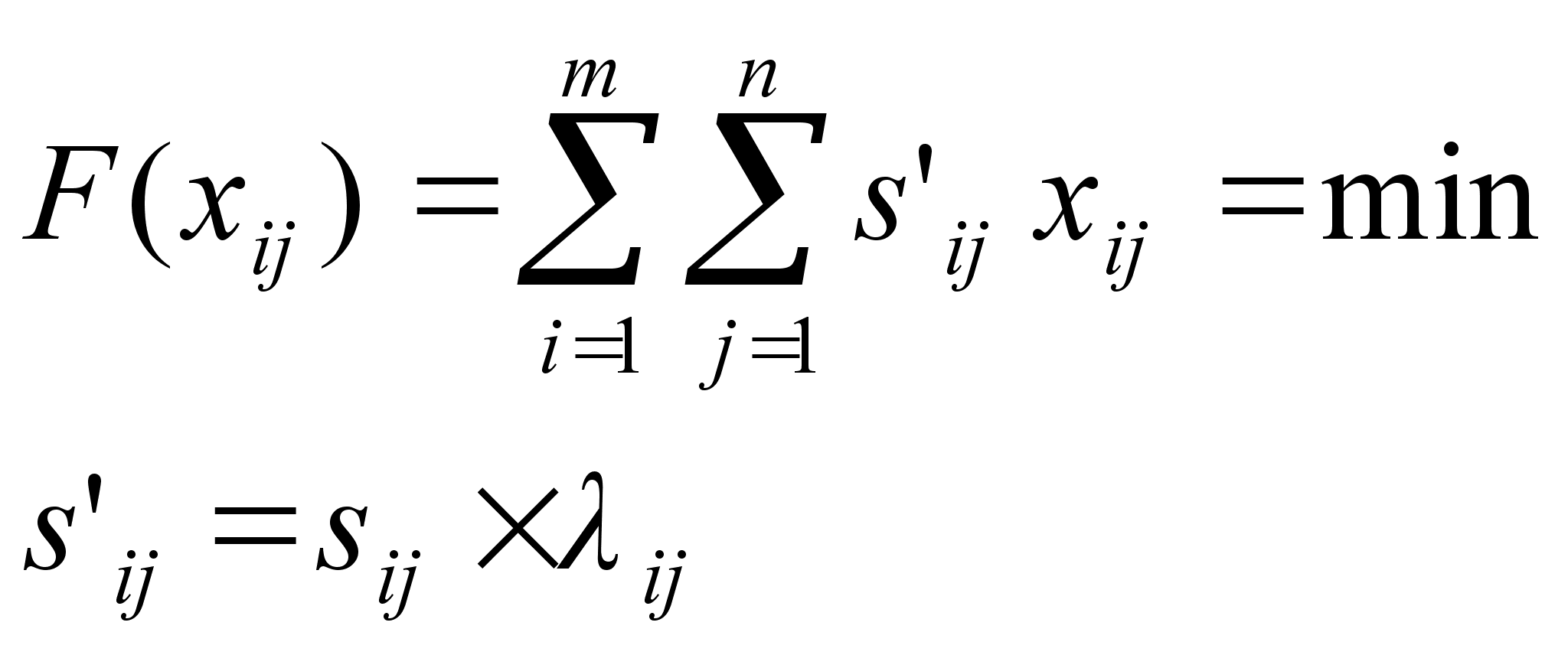
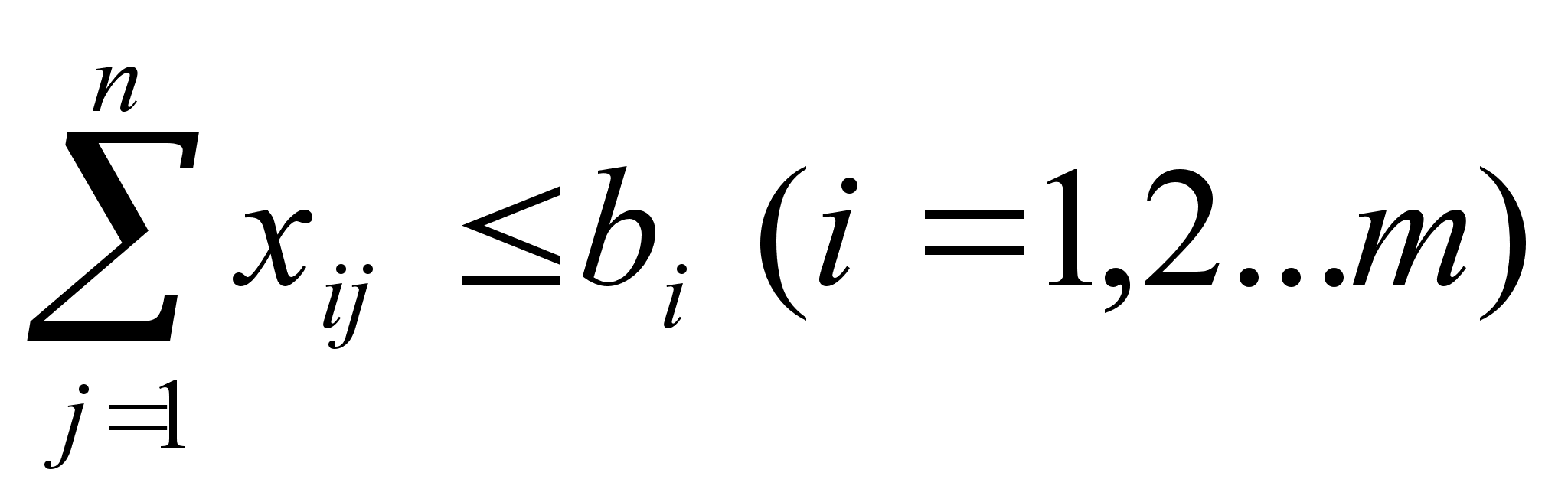
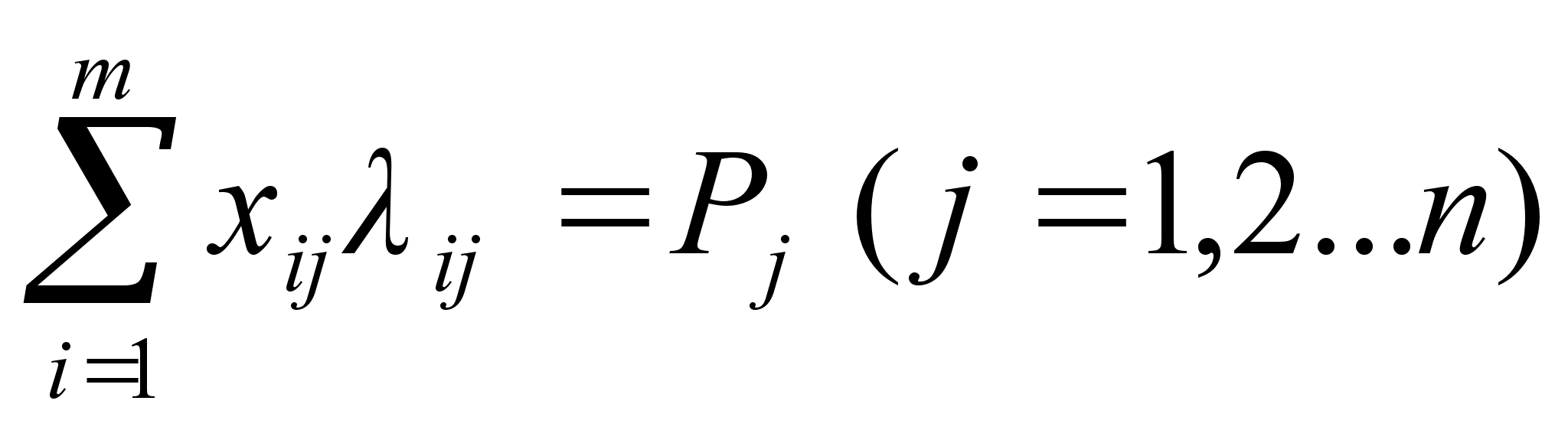
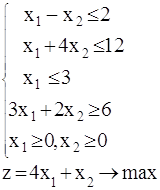

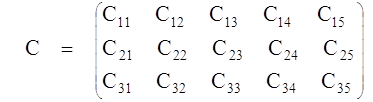
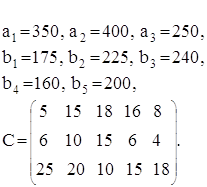
0 комментариев