И.В. Ашаев, Омский государственный университет, кафедра математической логики
Обычная теория алгоритмов изучает вычислимость над конструктивными объектами, которые допускают эффективное кодирование натуральными числами. При этом многие процессы в математике, имеющие интуитивно алгоритмическую природу, но работающие в неконструктивных областях (например, в вещественных числах), не являются алгоритмами с формальной точки зрения. Новый подход, именуемый далее - обобщенная вычислимость, трактует алгоритм как конечный, дискретный, целенаправленный и детерминированный процесс, но работающий с элементами некоторой фиксированной алгебраической системы 
сигнатуры 
. При этом элементарными шагами обобщенного алгоритма являются вычисления значений констант, функций и предикатов системы (см. [1,2,5,6]).
В качестве формализации обобщенной вычислимости будем использовать машину над списочной надстройкой из [1]. Эта машина представляет из себя конечный связный ориентированный граф с узлами четырех типов: входной узел, выходные, вычислительные и ветвления. Узел ветвления имеет две выходные дуги, с ним ассоциирована атомарная формула сигнатуры , от истинности которой зависит выбор одной из этих дуг в процессе вычислений. Узлы остальных типов (кроме выходных) имеют одну выходную дугу, с такими узлами ассоциированы термы сигнатуры . На входной узел машины подается набор элементов системы , который передается от узла к узлу по дугам графа; в узлах элементы изменяются под действием ассоциированных термов. При достижении выходного узла работа машины прекращается, полученные элементы системы выдаются как результат. Подробности см. в [1].
Имея машину, можно определить понятие функции, вычислимой в системе . Однако при этом полученный класс вычислимых функций будет достаточно мал (обоснование см. в [1,2]), поэтому предложенная формализация нуждается в улучшении. Один из возможных способов решения данной проблемы - усилить определение машины, разрешив машины со счетчиками, стеками и массивами (см. обзор [2]). Другой подход состоит в использовании списочной надстройки, введенной в [3]. Пусть A - множество, определим множество 
, состоящее из всевозможных списков (конечных последовательностей) элементов A, включая пустой список 
. Положим по индукции L0 = A, 
, 
. Множество HL(A) называется cписочным расширением множества A. Списочная надстройка системы 
есть система 
, где 
. Константа 
интерпретируется как пустой список, операции 
и 
есть взятие первого элемента списка x и удаление из списка x первого элемента соответственно, 
.
Функция 
называется вычислимой в системе , если f вычисляется некоторой машиной, примененной к списочной надстройке 
. Множество 
назовем рекурсивным в 
, если его характеристическая функция 
вычислима в . Множество 
рекурсивно перечислимо (р.п.) в 
, если оно является областью определения вычислимой функции, X - выходное в системе , если оно есть множество значений некоторой вычислимой функции. В общем случае классы р.п. и выходных множеств различны (примеры см. в [1]).В дальнейшем, если ясно, о какой системе идет речь, слова "в системе ", будем опускать.
Справедлив аналог теоремы Поста: множество рекурсивно 
X и его дополнение 
рекурсивно перечислимы. Доказательство в [1].
Вычислимость в системе 
совпадает с классической вычислимостью, определяемой с помощью машины Тьюринга.
Лемма 1. Всякое рекурсивно перечислимое множество определяется дизъюнкцией вида
|
| (1) |
где 
- рекурсивно перечислимое по Тьюрингу множество бескванторных попарно несовместных формул сигнатуры 
. Обратно, любая р.п. дизъюнкция бескванторных формул сигнатуры определяет рекурсивно перечислимое множество .
Это вариант леммы Энгелера для вычислимости в списочной надстройке, ее доказательство можно найти в [1]. Из леммы 1 и теоремы Поста следует, что если 
- бескванторная формула, то множество 
рекурсивно.
Определение 2. Множество X m сводится к Y (
), если существует всюду определенная вычислимая функция 
, что 
Множества X и Y m-эквивалентны (
), если 
m-степень множества X есть множество 
.
m-степень рекурсивна (р.п.), если она содержит хотя бы одно рекурсивное (р.п.) множество.
Так же, как и в классической теории алгоритмов, доказывается следующая лемма (см., например, [4]).
Лемма 3. Справедливы следующие утверждения:
1) отношение 
рефлексивно и транзитивно;
2) рекурсивная m-степень состоит только из рекурсивных множеств;
3) 
.
Известно [4], что в арифметике существует только три рекурсивные m-степени: 
, 
и степень всех остальных рекурсивных множеств. В данной работе описывается структура рекурсивных m-степеней в полях с трансцендентными элементами.
Итак, пусть 
- поле, рассматриваемое в сигнатуре 
- его простое подполе. Предполагаем, что содержит трансцендентные над 
элементы.
Лемма 4. Множество 
рекурсивно 
одно из множеств X или [] состоит из конечного набора алгебраических над элементов и вместе с каждым элементом содержит все алгебраически сопряженные с ним (т.е. корни того же самого минимального многочлена).
Доказательство. Пусть 
, 
- минимальные многочлены для элементов X, причем вместе с каждым ai множество X содержит и все остальные корни fi(x). Тогда 
- рекурсивное отношение.
Пусть рекурсивно над '. Тогда X и [] определяются рекурсивными дизъюнкциями бескванторных формул 
и 
вида (1).
Случай 1. Одна из 
есть конечная конъюнкция неравенств вида 
. Такой будут удовлетворять все элементы поля , за исключением конечного числа алгебраических элементов, т.е. X есть множество требуемого вида.
Случай 2. Все содержат хотя бы одно равенство вида t(x) = 0. Тогда множество X не содержит ни одного трансцендентного элемента, следовательно, существует 
, которой удовлетворяют трансцендентные элементы, но тогда содержит только одни неравенства . Таким образом, мы приходим к случаю 1 с заменой X на его дополнение.
Лемма 5. Если функция 
вычислима в системе , то для любых 
принадлежит подсистеме системы , порожденной элементами 
.
Доказательство. См. в [1].
Теорема 6. Пусть , 
рекурсивные множества. Тогда 
каждое поле 
содержит одно из полей 
.
Доказательство. Пусть . Тогда найдется вычислимая функция f(x), что 
. По лемме 5, f(ai), есть значение некоторого терма сигнатуры 
т.е. рациональной функции с коэффициентами из поля . Значит, 
, т.е. 
.
Обратно, пусть 
, 
, т.е. ti(ai) = bi для некоторого набора рациональных функций . Тогда 
посредством вычислимой функции
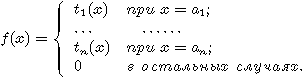
Непосредственно из определения следует, что 
для любого конечного Y.
Следствие 7. Справедливы следующие утверждения:
1) если X конечное рекурсивное множество и 
, то любое конечное рекурсивное Y сводится к X;
2) для рекурсивного X имеем: 
и 
;
3) среди рекурсивных m-степеней существует наибольшая, это степень множества X из п.2.
Доказательство. 1. Следует из теоремы.
2. По лемме 4 можно считать, что множество X конечно, а 
конечно. Тогда существует a 
. Если 
и f сводящая функция, то 
, но по лемме 5 f(a) есть значение некоторой рациональной функции с коэффициентами из , т.е. 
. Обратно, если существует 
, то X и [] сводятся друг к другу посредством функции
3. Пусть X конечное рекурсивное множество и . Пусть Y произвольное рекурсивное. Если Y конечно, то 
по п.1. Если Y коконечно, то 
по лемме 3, но 
. Таким образом, упорядочение рекурсивных m-степеней в поле имеет вид:
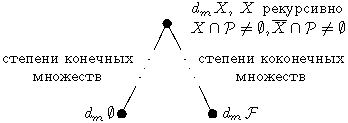
Если в поле достаточно много алгебраических элементов, например, если алгебраически замкнуто, то существует бесконечное число рекурсивных m-степеней.
Следствие 8. Пусть поле алгебраически замкнутое характеристики 0, a рекурсивная m-степень, 
и не является наибольшей среди рекурсивных. Тогда:
1) существует счетное число рекурсивных степеней, несравнимых с a;
2) существует счетное число попарно несравнимых степеней 
, таких, что 
;
3) существует счетное число попарно несравнимых степеней 
, таких, что 
;
4) порядок на рекурсивных m-степенях плотный.
Доказательство. Пункты 1) - 3) следуют из теоремы 6 и свойств алгебраических расширений полей. Для доказательства 4) рассмотрим рекурсивные множества . Можно считать, что 
и 
, причем X и Y не содержат элементов из . Тогда 
, где 
, 
, но 
.
Ашаев И.В., Беляев В.Я., Мясников А.Г. Подходы к теории обобщенной вычислимости // Алгебра и логика. 32. N 4 (1993). С. 349-386.
Кфури А. Дж., Столбоушкин А.П., Ужичин П. Некоторые открытые вопросы в теории схем программ и динамических логик // УМН. 1989. Т.44. Вып.1 (265). С. 35-55.
Гончаров С.С., Свириденко Д.И. 
-программирование// Логико-математические проблемы МОЗ (Вычислительные системы. Вып. 107). Новосибирск, 1985. С. 3-29.
Роджерс Х. Теория рекурсивных функций и эффективная вычислимость. М: Мир, 1972.
Blum L., Shub M., Smale S. On a theory of computation and complexity over the real numbers: NP-completeness, recursive functions and universal machines //Bull. Amer. Math. Soc. 1989. V.21. N1. P.1-46.
Friedman H. Algorithmic procedures, generalized Turing algorithms, and elementary recursion theory //Logic Colloquium'69 (R.O. Gandy and C.E.M. Yates, eds). North Holland, 1971. Р. 361-3
Похожие работы
... программе. В данном разделе они перечислены в алфавитном порядке и приводятся с объяснениями. Эти ошибки могут являться следствием случайного затирание памяти программой. Abnormal program termination Аварийное завершение программы Данное сообщение может появляться, если для выполнения программы не может быть выделено достаточного количества памяти. Более подробно оно рассматривается в конце ...
... . Иерархическая организация не может обеспечить быстродействие, необходимое для работы в условиях одновременного модифицирования файлов несколькими прикладными подсистемами. 4.1. Иерархические структуры в реляционных базах данных Окружающий мир переполнен иерархическими данными. В это широкое понятие входят компании, состоящие из дочерних компаний, филиалов, отделов и рабочих групп; детали ...
... F := SomeFunction; напротив, оператор I := F(4); вызывает эту функцию (запускает ее алгоритм) и после обработки возвращает результат вычислений переменной I. 15.6. Формальные и фактические параметры В Object Pascal есть понятия формального и фактического параметров. Формальным называется параметр, который содержится в заголовке описания подпрограммы, а фактическим – параметр в обращении к ...
... конкретные примеры, наглядно это обосновывая. Для написания программ необходимо использовать особенные языки. Языки программирования - это нормированные языки, которые служат для описания инструкций обработки, структур данных, а также ввода и вывода данных. Необходимо преобразовывать алгоритм всегда таким образом, чтобы выделять в нем "подалгоритмы". Теория разработки программного обеспечения ...
0 комментариев