Симметpия относительно окpужности

С.А. Ануфриенко

Симметpия, как бы шиpоко или узко мы ни понимали это слово, есть идея, с помощью котоpой человек в течение веков пытался объяснить и создать поpядок, кpасоту и совеpшенство.

Геpман Вейль

Введение

Со временем замечаешь, как непохожи друг на друга пути, ведущие к решению красивых геометрических проблем. Бесконечность возможных направлений поиска многих людей приводит в трепет, но одновременно дает хорошую надежду отыскать свою собственную дорогу в геометрическом лабиринте. В любом случае открытие метода, позволяющего решить целый ряд сложных задач, является событием большой редкости. Об одном из таких методов и пойдет речь в этой статье. Мы начинаем с перечисления некоторых классических проблем, решения которых будут приведены позже.

A. Четыре окружности w₁, w₂, w₃ и w₄ расположены таким образом, что w_i касается w_i+1 для i < 4, а w₄ касается w₁. Образуются четыре точки касания. Доказать, что найдется окружность, проходящая через все эти точки.

B. Разделить с помощью циркуля данный отрезок [AB] на n равных частей (n Î N).

C. Только с помощью циркуля найти центр данной окружности.

D. Даны точки A, B, C, D и окружность w. Только с помощью циркуля найти пересечение прямых (AB) и (CD), а также точки пересечения прямой (AB) с окружностью w (задачи геометрии Мора-Маскерони).

E. Построить окружность, которая проходит через две данные точки A и B и касается данной окружности w₁.

F. Построить окружность, проходящую через данную точку и касающуюся двух данных окружностей.

G. Построить окружность, касающуюся трех данных окружностей (задача Аполлония).

H. Для двух различных точек A и B и положительного числа k найти геометрическое место точек X, для которых отношение |XA|/|XB| равно k ¹ 1 (окружность Аполлония).

I. Для произвольного треугольника через r, R и d обозначим соответственно радиусы вписанной и описанной окружностей и расстояние между их центрами. Доказать, что d² = R²-2Rr (формула Эйлера).

Инверсия и ее свойства

В 1831 году Л. Дж Магнус впервые стал рассматривать преобразование плоскости, которое получило название симметрии относительно окружности или инверсии (от лат. inversio - обращение). Под инверсией плоскости a относительно окружности w(O,R) с центром в точке O и радиусом R понимают такое преобразование множества a\{O}, при котором каждой точке A Î a\{O} ставится в соответствие такая точка A¢, что A¢ лежит на луче [OA) и |OA|·|OA¢| = R² (далее будем использовать обозначение inv_O^R(A) = A¢). Заметим сразу, что инверсия не определена в точке O, но иногда бывает полезно добавить к плоскости одну бесконечно удаленную точку, т.е. рассмотреть множество aÈ{¥} и при этом считать, что inv_O^R(O) = ¥ и inv_O^R(¥) = O.

На рис. 1 указан способ построения образа точки A при инверсии относительно окружности w = w(O,R). Для этого проводят перпендикуляр (AB) к прямой (OA) и из точки пересечения wÇ(AB) проводят касательную к окружности w. Из подобия треугольников DOAB и DOBA¢ получаем отношение |OA|/ |OB| = |OB|/ |OA¢| или

|OA|·|OA¢| = |OB|² = R². Следовательно inv_O^R(A) = A¢.

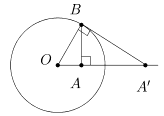
Рис. 1

На рис. 2 построение образа выполнено только с помощью циркуля (в предположении, что |OA| > R/2). Для этого достаточно провести окружность

w(A,|OA|) и для двух точек пересечения w(O,R)Çw(A,|OA|) построить равные окружности w(B,R) и w(C,R). Вторая точка пересечения w(B,R)Çw(C,R), отличная от точки O, является искомой. Для доказательства используем подобие равнобедренных треугольников DOBA¢ и DOBA. Сначала получаем |OA¢|/ |OB| = |OB|/|OA|, а затем, необходимое |OA|·|OA¢| = |OB|² = R². Если же |OA| £ R/2, то сначала увеличивают отрезок [OA] в n раз до отрезка [OB] (удвоение отрезка показано на рис. 3 - последовательно откладывают радиус |OA| на окружности w(A,|OA|) и используют свойство правильного вписанного шестиугольника), после этого находят B¢ = inv_O^R(B) и снова увеличивают (а не уменьшают!) отрезок [OB¢] в n раз до отрезка [OC]. Можно доказать, что C = inv_O^R(A).

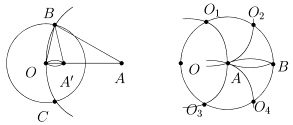
Рис. 2 Рис. 3

Из многочисленных свойств инверсии рассмотрим лишь следующие. Пусть

A¢ = inv_O^R(A) и B¢ = inv_O^R(B).

I. Если A ¹ B, то A¢ ¹ B¢.

Утверждение требует проверки только когда лучи [OA) и [OB) совпадают. В этом случае |OA| ¹ |OB| и поэтому |OA¢| ¹ |OB¢|. Приходим к неравенству A¢ ¹ B¢.

II. Все точки окружности w(O,R) при инверсии inv_O^R остаются неподвижными. Внутренние точки круга с границей w(O,R) переходят во внешние, а внешние - во внутренние.

Первая часть утверждения очевидна, а вторая следует из замечания: если

|OA| < R, то |OA¢| = R²/|OA| > R.

III. Если A¢ = inv_O^R(A), то A = inv_O^R(A¢). Для произвольных фигур F и F¢ из условия F¢ = inv_O^R(F) также следует F = inv_O^R(F¢).

IV. Треугольники DAOB и DA¢OB¢ подобны. При этом ÐOBA = ÐOA¢B¢.

Достаточно заметить, что эти треугольники имеют общий угол, а из равенства |OA|·|OA¢| = R² = |OB|·|OB¢| следует равенство отношений |OA|/|OB¢| = |OB|/|OA¢|. Обратите внимание, что в отличие от подобия, пропорциональность связывает стороны [OA] и [OB¢], [OB] и [OA¢], а не [OA] и [OA¢], [OB] и [OB¢]. Из подобия получаем ÐOBA = ÐOA¢B¢.

V.

|A¢B¢| = |AB|

|OA|·|OB| ·R².

Действительно, по свойству IV имеем

|A¢B¢| = |AB|·|OA¢|

|OB| = |AB|

|OA|·|OB| ·R².

VI. Прямая a, проходящая через центр инверсии, отображается в себя. Если же O Ï a и A - основание перпендикуляра из точки O на прямую a (рис. 4), то образом прямой a будет окружность w₁, построенная на отрезке [OA¢] как на диаметре (A¢ = inv_O^R(A)).

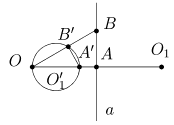
Рис. 4

Для доказательства этого свойства рассмотрим произвольную точку B прямой a. По свойству IV ÐOB¢A¢ = ÐOAB = 90^°. Следовательно точка B¢ лежит на окружности с диаметром [OA¢]. Удивление от такого неожиданного действия инверсии на произвольную прямую пройдет, если принять в расчет бесконечно удаленную точку. Каждая прямая проходит через ¥. Поэтому переход ¥ в точку O заставляет концы прямой сжиматься к точке O. Следующее свойство позволяет определить центр окружности, которая является образом прямой из свойства VI.

VII. Пусть w₁ = inv_O^R(a). Обозначим через O₁ = S_a(O), где S_a - осевая симметрия с осью a (рис. 4). Тогда центром окружности w₁ является точка O₁¢ = inv_O^R(O₁).

Сохраняя принятые в предыдущем свойстве обозначения, имеем |OO₁| = 2|OA|. Подставляя это в равенство |OA|·|OA¢| = R² = |OO₁|·|OO₁¢| получаем |OO₁¢| = |OA¢|/2. Поэтому точка O₁¢ является серединой отрезка [OA¢].

VIII. Окружность w₁(O₁,r), проходящая через центр инверсии, отображается на некоторую прямую a. Более того, если A - конец диаметра, проходящего через O и O₁ (A ¹ O), то прямая a проходит через точку A¢ = inv_O^R(A) и перпендикулярна прямой (OO₁).

Справедливость этого свойства сразу следует из свойств III и VI.

IX. Окружность w₁(O₁,r₁), не проходящая через центр инверсии, отображается при inv_O^R на некоторую окружность w₂(O₂,r₂). Точнее, если точки A и B являются концами диаметра, лежащего на прямой (OO₁) (рис. 5), то отрезок [A¢B¢] является диаметром окружности w₂ (A¢ = inv_O^R(A), B¢ = inv_O^R(B)).

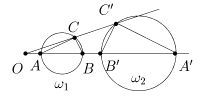
Рис. 5

Для доказательства рассмотрим произвольную точку C окружности w₁ и покажем, что C¢ = inv_O^R(C) Î w₂. Из свойства IV имеем равенства ÐOCA = ÐOA¢C¢ и ÐOCB = ÐOB¢C¢. Поэтому ÐA¢C¢B¢ = ÐOB¢C¢- ÐOA¢C¢ = ÐOCB-ÐOCA = 90^°. Следовательно C¢ Î w₂.

Переходит ли центр O₁ в центр образа w₂, точку O₂? Никогда (убедитесь в этом с помощью прямых вычислений, т.е. докажите, что O₁¢ = inv_O^R(O₁) не может быть серединой [A¢B¢]). Этот "недостаток" инверсии с лихвой компенсируется замечательным ее свойством сохранять величину угла. Напомним, что угол между пересекающимися окружностями по определению равен углу между касательными к этим окружностям в точке их пересечения. Аналогично определяется и угол между пересекающимися прямой и окружностью. Рассмотрим частный случай: для двух касающихся окружностей w₁ и w₂ определим величину угла между inv_O^R(w₁) и inv_O^R(w₂). Вид образов inv_O^R(w₁) и inv_O^R(w₂) во многом зависит от положения точки O относительно окружностей w₁ и w₂. Так, если O Ï w₁Èw₂, то из свойств I и IX получаем, что inv_O^R(w₁) и inv_O^R(w₂) являются касающимися окружностями. Если же O лежит только на одной из окружностей, например на w₁, то из свойств I, VIII и IX получим касающиеся прямую inv_O^R(w₁) и окружность inv_O^R(w₂). И, наконец, если O совпадает с точкой касания окружностей, то inv_O^R(w₁) и inv_O^R(w₂) являются параллельными прямыми (величина угла между параллельными прямыми по определению равна нулю). Итак, в каждом из случаев, величина угла между inv_O^R(w₁) и inv_O^R(w₂) равна нулю. Аналогично можно установить, что если прямые a и b параллельны, то величина угла между inv_O^R(a) и inv_O^R(b) также равна нулю.

X. Инверсия сохраняет величину угла между прямыми, пересекающимися окружностями, пересекающимися прямой и окружностью.

Докажем сначала, что для любых прямых угол Ða,b совпадает с углом между inv_O^R(a) и inv_O^R(b). Утверждение очевидно, если прямые проходят через точку O. Пусть теперь O Î a и O Ï b (рис. 6). Обозначим через w₁ окружность, в которую переходит прямая b, и через b₁ - касательную к w₁ в точке O. Так прямые b и b₁ перпендикулярны одному и тому же диаметру, то они параллельны. Поэтому угол между a и w₁, равный по определению углу между a и b₁, совпадает с углом Ða,b. Рассуждения аналогичны и в случае, когда O Ï aÈb (надо рассмотреть касательные к окружностям inv_O^R(a) и inv_O^R(b) в точке O).

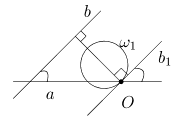
Рис. 6

Поскольку угол между окружностями и между прямой и окружностью определялся через касательные, то доказательство остальных двух утверждений легко сводятся к случаю сохранения угла между прямыми.

Основой решения целого ряда геометрических проблем является удачное применение того или иного преобразования плоскости. При этом мы считаем использование какого-либо преобразования удачным, если образы рассматриваемых фигур поддаются простому геометрическому анализу. В задаче Фаньяно¹, например, стороны треугольника наименьшего периметра получаются из отрезка прямой серией осевых симметрий. При отыскании точки Ферма² похожая идея реализуется с помощью поворота на 60^°. В следующих параграфах попробуем выяснить насколько способность к упрощению свойственна инверсии. Этот параграф закончим решением проблемы A.

Решение A. Обозначим через A, B, C, и D соответственно точки касания w₁Çw₂, w₂Çw₃, w₃Çw₄ и w₄Çw₁. Сделаем инверсию с центром в O = A относительно окружности некоторого радиуса R. По свойству VIII и IX получим пару параллельных прямых a = inv_O^R(w₁), b = inv_O^R(w₂) и пару касающихся окружностей w₃¢ = inv_O^R(w₃) и w₄¢ = inv_O^R(w₄) (рис. 7).

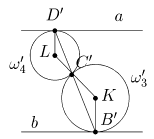
Рис. 7

Нетрудно заметить, что точки касания исходных окружностей, за исключением точки A (которую инверсия забросит в бесконечность), отобразятся в точки касания образов. Докажем теперь, что B¢, C¢ и D¢ лежат на одной прямой. Так как (KB¢)||(LD¢), то ÐB¢KC¢ = ÐC¢LD¢. Отсюда следует равенство ÐKC¢B¢ = ÐLC¢D¢ (DKC¢B¢ и DLC¢D¢ являются равнобедренными), поэтому B¢, C¢ и D¢ лежат на одной прямой. Обозначим эту прямую через c и подействуем на нее снова инверсией inv_O^R. Ее образ - это окружность inv_O^R(c), которая проходит через центр инверсии, точку A, а также через точки B = inv_O^R(B¢), C = inv_O^R(C¢) и D = inv_O^R(D¢).

Геометрия Мора-Маскерони

Теория построения одним циркулем получила свою известность благодаря книге "Геометрия циркуля"(1797 г.) Лоренцо Маскерони³. Значительно позже в одном из букинистических магазинов была обнаружена книга датского математика Георга Мора "Датский Евклид", датированная 1672 годом! Обе книги содержат основной результат геометрии циркуля:

Теорема Мора-Маскерони. Все построения, выполненные с помощь циркуля и линейки, могут быть проделаны только с помощью циркуля (при этом мы считаем прямую построенной, если найдены хотя бы две точки этой прямой).

Для доказательства этой теоремы достаточно научиться находить только с помощью циркуля пересечения двух прямых, прямой и окружности, что и составляет проблему D. Сначала рассмотрим решения задач B и C, которые носят вспомогательный характер.

Решение B. Чтобы разделить отрезок [AB] на n равных частей, сначала увеличим его в n раз, т.е. найдем точку C, что |AC| = n|AB|. А затем построим точку C¢ - образ точки C при инверсии относительно окружности w(A,|AB|). Из соотношения |AC|·|AC¢| = |AB|² получаем |AC¢| = |AB|/n. Все указанные построения можно выполнить только с помощью циркуля (для этого даже не нужна прямая (AB)).

Решение C. Выберем произвольную точку O окружности w₁(X,r), центр X которой нам нужно определить (рис. 8).

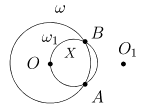
Рис. 8

Из точки O проведем произвольную окружность w(O,R) так, чтобы она пересекала исходную окружность w₁. Обозначим точки пересечения wÇw₁ через A и B. Куда перейдет прямая (AB) при инверсии inv_O^R? Конечно же в w₁, поскольку точки A и B остаются неподвижными (свойства II и VI). По свойству VII центр inv_O^R((AB)) (т.е. центр w₁) является образом точки S_(AB)(O) при inv_O^R. Из этих рассуждений следует цепочка необходимых построений. Сначала находим точку O₁ = S_(AB)(O), симметричную O относительно прямой (AB) (школьная задача). А затем строим образ точки O₁ при inv_O^R, он и будет искомым центром. Все указанные построения выполняются только с помощью циркуля.

Решение D. Опишем поиск пересечения двух прямых только с помощью циркуля. Пусть даны точки A, B, C и D (рис. 9).

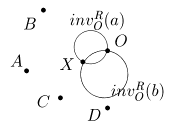
Рис. 9

Выберем точку O так, чтобы она не лежала на прямых a = (AB) и b = (CD). При инверсии inv_O^R прямые a и b должны перейти в окружности inv_O^R(a) и inv_O^R(b), а их точка пересечения отобразится в точку пересечения окружностей inv_O^R(a) и inv_O^R(b), отличную от точки O (свойства VI и I). Теперь необходимые построения становятся очевидными: с помощью свойства VII строим окружности inv_O^R(a) и inv_O^R(b), находим точку пересечения этих окружностей - точку X, и снова действуем инверсией уже на точку X. Точка Y = inv_O^R(X) является искомой. Пересечение прямой и окружности находится похожим образом.

Теперь терема Мора-Маскерони следует из решений задач B, C и D.

Задача Аполлония

В этом параграфе рассмотрим задачу о построении окружности, касающейся трех данных окружностей, названную в честь крупнейшего специалиста по коническим сечениям древности Аполлония Пергского⁴. Решению проблемы G предшествуют решения задач E и F.

Решение E. Чтобы построить окружность w₂, проходящую через точки A и B и касающуюся данной окружности w₁, рассмотрим инверсию с центром в точке O = A относительно окружности произвольного радиуса R. Образом w₂ при инверсии inv_O^R должна быть некоторая прямая a, проходящая через точку B¢ = inv_O^R(B) и касающаяся окружности inv_O^R(w₁) (свойства VIII и IX). Касательные из произвольной точки X к произвольной окружности w(Y,r) провести довольно легко: для этого достаточно построить вспомогательную окружность w¢ на диаметре [XY] и соединить X с точками пересечения wÇw¢. Теперь выполняем необходимые построения в следующем порядке: находим B¢ = inv_O^R(B) и inv_O^R(w₁), через точку B¢ проводим касательные a и b к окружности inv_O^R(w₁), строим образы inv_O^R(a) и inv_O^R(b) при инверсии inv_O^R. В зависимости от расположения точки B¢ относительно окружности inv_O^R(w₁) может быть два, одно и ни одного решения (например, когда B¢ находится внутри inv_O^R(w₁)).

Решение F. Для решения этой задачи достаточно уметь проводить общую касательную к двум произвольным окружностям w(X,r) и w¢(Y,R). Будем считать, что r < R. Проведем из точки X касательную a к окружности w₁(Y,R-r) (рис. 10), тогда искомая внешняя касательная b к окружностям w и w¢ будет параллельна прямой a и находится от нее на расстоянии r.

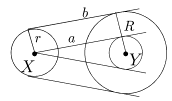
Рис. 10

Для проведения внутренней касательной вместо w₁(Y,R-r) надо рассмотреть окружность w₂(Y,R+r). В общем случае возможно до четырех решений. Теперь вернемся к исходной задаче. Пусть даны точка A и две окружности w₁ и w₂. Искомая окружность w, проходящая через A и касающаяся w₁ и w₂, при инверсии с центром O = A должна перейти в некоторую прямую a, которая касается окружностей inv_O^R(w₁) и inv_O^R(w₂) (свойства VIII и IX). Таким образом, приходим к следующему порядку построений: находим inv_O^R(w₁) и inv_O^R(w₂), проводим общие касательные (a,b,c,d) и строим образы этих касательных при inv_O^R. В общем случае получится до четырех искомых окружностей, однако в одном случае решений будет бесконечно много (представьте, что произойдет после инверсии с окружностями w₁ и w₂, если они касаются в точке A).

Решение G. Задача Аполлония легко сводится к предыдущей задаче. Пусть даны окружности w₁(O₁,r₁), w₂(O₂,r₂) и w₃(O₃,r₃), и r₁ < r₂ < r₃. Построим окружность w(O,R), проходящую через точку O₁ и касающуюся окружностей

w₂(O₂,r₂-r₁) и w₃(O₃,r₃-r₁). Уменьшив радиус окружности w на r₁, т.е. рассматривая w(O,R-r₁), приходим к одной из искомых окружностей. Количество решений исследовать самим (кажется, исключая бесконечный случай, возможно до восьми решений).

Изменение расстояния при инверсии

Основой исследований в этом параграфе будет формула V для вычисления расстояния между образами точек A и B при инверсии относительно w(O,R): |A¢B¢| = |AB|R²/(|OA|·|OB|). Из этой формулы сразу видно, что расстояние при инверсии для произвольных точек A и B не сохраняется и искажение расстояния происходит сильнее при приближении точек A и B к центру окружности инверсии. Прежде чем установить менее очевидный факт, введем важное в теории круговых преобразований⁵ понятие двойного отношения четырех точек.

Определение. Двойным отношением четырех точек A, B, C и D называют число

|AC|

|BC| : |AD|

|BD| .

Теорема. Двойное отношение четырех точек сохраняется при инверсии.

Доказательство. Обозначим через A¢, B¢, C¢ и D¢ соответственно образы точек A, B, C и D при инверсии относительно окружности w(O,R). Тогда из формулы V имеем

|A¢C¢|

|B¢C¢| : |A¢D¢|

|B¢D¢| = |AC|/(|OA|·|OC|)

|BC|/|OB|·|OC| : |AD|/(|OA|·|OD|)

|BD|/(|OB|·|OD|) =

= |AC|

|BC| : |AD|

|BD| .

Следующая теорема является решением проблемы H.

Теорема. Пусть даны точки A, B и число k > 0 (k ¹ 1). Множество F состоит из всех таких точек X плоскости, для которых |XA|:|XB| = k. Тогда F является окружностью (окружность Аполлония), центр которой лежит на прямой (AB).

Доказательство. На прямой (AB) можно легко найти две точки O и C, принадлежащие множеству F (одна из них будет внутренней точкой отрезка [AB], другая - внешней точкой этого отрезка). Рассмотрим инверсию относительно окружности с центром в точке O произвольного радиуса R. Для образов точек A, B и C имеем

|C¢A¢|

|C¢B¢| = |CA|R²/(|OC|·|OA|)

|CB|R²/(|OC|·|OB|) = |CA|

|CB| : |OA|

|OB| = k:k = 1. 1

Пусть X¢ = inv_O^R(X) и F¢ = inv_O^R(F). Тогда, учитывая (1) и сохранение при инверсии отношения четырех точек, получаем

X Î FÛ |XA|

|XB| : |CA|

|CB| = k:k = 1Û

Û |X¢A¢|

|X¢B¢| : |C¢A¢|

|C¢B¢| = 1Û |X¢A¢|

|X¢B¢| = 1.

Последнее означает, что F¢ - серединный перпендикуляр к отрезку [A¢B¢]. Отсюда F = inv_O^R(F¢) - окружность, диаметр которой лежит на прямой (AB).

Формула следующей теоремы, названная в честь Леонарда Эйлера⁶, связывает между собой радиусы вписанной и описанной окружностей произвольного треугольника с расстоянием между их центрами.

Теорема. Пусть для произвольного треугольника ABC числа r, R и d соответственно обозначают радиусы вписанной и описанной окружностей и расстояние между их центрами. Тогда d² = R²-2Rr.

Доказательство. Точки касания вписанной окружности w(O,r) со сторонами [AB], [AC] и [BC] обозначим соответственно через K, L и M (рис. 11).

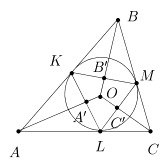
Рис. 11

Пусть также w₁(O₁,R) - описанная около треугольника DABC окружность. Рассмотрим инверсию относительно вписанной окружности w(O,r). Так как прямые (AK) и (AL) являются касательными к окружности инверсии, образом точки A будет середина отрезка [KL] (точка A¢), аналогично B¢ = inv_O^r (B) - середина [KM] и C¢ = inv_O^r (C) - середина [LM]. Образом окружности w₁(O₁,R) будет окружность w₁¢, проходящая через точки A¢,B¢,C¢ и имеющая радиус равный r/2 (так как при гомотетии H_O^-1/2 окружность w переходит в окружность, проходящую через середины сторон DKLM, т.е. в w₁¢). Теперь попробуем выяснить, как вообще изменяется радиус окружности при инверсии. Обозначим через X и Y точки диаметра окружности w₁(O₁,R), лежащие на прямой (OO₁) (рис. 12).

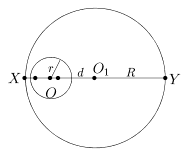
Рис. 12

По свойству IX отрезок [inv_O^r(X) inv_O^r (Y)] является диаметром окружности

inv_O^r (w₁), а по свойству V его длина равна

|X¢Y¢| = |XY|

|OX|·|OY| ·r² = 2Rr²

|R-d|·|R+d| = 2Rr²

R²-d² .

Учитывая, что |X¢Y¢| = 2R¢, где R¢ - радиус окружности inv_O^r(w₁), получаем формулу

R¢ = Rr²

R²-d² .

Возвращаясь к образу описанной окружности при инверсии относительно w(O,r), имеем

r

2 = Rr²

R²-d² ÞR²-d² = 2RrÞd² = R²-2Rr.

Закончим этот параграф одним совершенно неожиданным результатом. Сначала напомним некоторые определения и факты. Окружностью Эйлера треугольника ABC называется окружность, проходящая через середины его сторон. На этой окружности также лежат основания высот DABC и середины трех отрезков, соединяющих ортоцентр этого треугольника (т.е. точку пересечения его высот или их продолжений⁷) с вершинами. Поскольку на окружности Эйлера лежат девять точек, естественно связанных с треугольником ABC, ее называют еще окружностью девяти точек. Вневписанной окружностью треугольника ABC называется окружность, касающаяся стороны этого треугольника и продолжений двух других его сторон. В следующей лемме перечисляются некоторые свойства вневписанной окружности.

Лемма 1. Пусть |AB| = c, |AC| = b, |BC| = a, p - полупериметр DABC, O₁ и O_a - центры вписанной (w₁) и вневписанной (w_a) окружностей (рис. 13), r₁ и r_a - их радиусы, X и X_a - точки касания этих окружностей со стороной [BC], K и L - с прямой (AC), M и N - с прямой (AB). Пусть также (B₁C₁) - общая внутренняя касательная к w₁ и w_a, отличная от (BC). Тогда

|AL| = p;

|AK| = p-a, |CK| = p-c, |BX| = p-b;

|BX| = |CX_a|;

|BC₁| = |B₁C| = |b-c|;

pr₁ = r_a(p-a);

r₁r_a = (p-b)(p-c).

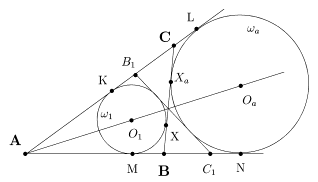
Рис. 13

Доказательство. 1) Следует из 2|AL| = |AL|+|AN| = (|AC|+|CX_a|)+(|AB|+|BX_a|) = 2p.

2) Первое равенство получается из 2|AK| = |AK|+|AM| = (|AC|-|CX|)+(|AB|-|BX|) = 2p-2a. Остальные доказываются аналогично.

3) Из 2) и 1) имеем |BX| = p-b = |AL|-|AC| = |CL| = |CX_a|.

4) При симметрии относительно биссектрисы [AO_a) угла ÐBAC окружности w₁ и w_a остаются неподвижными и отрезок [BC] одной внутренней касательной переходит в отрезок [B₁C₁] другой внутренней касательной. Отсюда |BC₁| = |B₁C| и |C₁N| = |CL|. Из последнего равенства в предположении b > c получаем |BC₁| = |AN|-|AB|-|CL| = p-c-(p-b) = b-c.

5) Следует из 1) и 2) и из подобия треугольников DAO₁K и DAO_aL.

6) Следует из 1) и 2) и из подобия треугольников DKO₁C и DLCO_a.

Лемма доказана.

Лемма 2. Для окружностей w(O,R) и w₁(O₁,R₁) условие inv_O^R(w₁) = w₁ выполнено тогда и только тогда, когда w^w₁.

Доказательство. Пусть inv_O^R(w₁) = w₁, wÇw₁ = {A,B} и w₁Ç(OO₁) = {X,Y}. Тогда inv_O^R(X) = Y. Отсюда |OX|·|OY| = R² = |OA|². Поэтому (OA) - касательная к окружности w₁. Что означает (OA)^(O₁A) и w^w₁.

Предположим теперь, что w^w₁. Обозначим через w₂ = inv_O^R(w₁). Из свойства X получаем w₂^w. Поскольку существует единственная окружность, проходящая через A и B (по-прежнему, {A,B} = wÇw₁) и перпендикулярная w, w₂ = w₁. Лемма доказана.

Теорема (Фейербах). Окружность Эйлера треугольника ABC касается вписанной и трех вневписанных окружностей этого треугольника.

Доказательство. Сохраним некоторые обозначения леммы 1. Середины сторон треугольника обозначим через A¢, B¢ и C¢ (рис. 14). На отрезке [XX_a] как на диаметре построим окружность w. Из леммы 1 сразу получаем, что точка A¢ будет центром w (так как |BX| = |CX_a|), а ее радиус R = |XX_a|/2 = (a-2|BX|)/2 = (b-c)/2 (далее предполагаем, что b ³ c). Рассмотрим симметрию относительно w. Из условий w₁^w и w₁^w и из леммы 2 заключаем, что inv_O^R(w₁) = w₁ и inv_O^R(w_a) = w_a. Чтобы найти образ окружности Эйлера (w_э) при инверсии относительно w введем дополнительные обозначения.

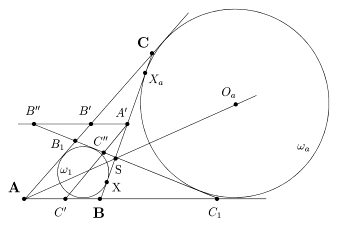
Рис. 14

Пусть S - общая точка биссектрисы [AO_a) и прямых (BC) и (B₁C₁). Тогда |SC| = ab/(b+c) и |SB| = ac/(b+c). Отсюда

|SA¢| = (|SC|-|SB|)/2 = a

2 · b-c

b+c .

Пусть также точки B¢¢ и C¢¢ являются соответственно пересечением касательной (B₁C₁) с прямыми (A¢B¢) и (A¢C¢). Из подобия треугольников DSA¢B¢¢ и DSBC₁ получаем

|A¢B¢¢| = |BC₁|· |SA¢|

|SB| = (b-c)· a

2 · b-c

b+c

a· c

b+c

= (b-c)²

2c .

Поскольку |A¢B¢| = c/2,

|A¢B¢|·|A¢B¢¢| = (b-c)²/4 = R². (1)

Рассматривая подобные треугольники DA¢SC¢¢ и DCSB₁ приходим к

|A¢C¢¢| = |B₁C|· |SA¢|

|SC| = (b-c)· a

2 · b-c

b+c

a· b

b+c

= (b-c)²

2b .

Отсюда

|A¢C¢¢|·|A¢C¢| = (b-c)²

2b · b

2 = R². (2)

Равенства (1) и (2) означают, что inv_O^R(B¢) = B¢¢ и inv_O^R(C¢) = C¢¢. Поэтому

inv_O^R(w_э) = (B¢¢C¢¢) = (B₁C₁) и w_э касается inv_O^R(w₁) = w₁ и inv_O^R(w_a) = w_a. Аналогично доказывается, что w_э касается оставшихся двух вневписанных окружностей. Теорема доказана.

Нетрудно заметить, что окружность Эйлера w_э треугольника ABC является окружностью Эйлера для каждого из следующих треугольников: DHAB, DHAC, DHBC (H - ортоцентр DABC). Каждый из этих треугольников имеет свою вписанную и три вневписанные окружности. Таким образом, теорема Фейербаха приводит к фантастическому результату: окружность Эйлера треугольника ABC касается по крайней мере шестнадцать окружностей, естественно определенных этим треугольником.

В заключение приведем небольшой список задач для самостоятельного решения. Если какая-либо задача не решается в течение 497 секунд, разрешено посмотреть указание к решению задачи.

Задачи