Навигация
![]() 18.10.2010
18.10.2010
Лекция 1
Волны
1. Введение
2. Что такое волна. Какие бывают волны
2.1. Синусоидальные волны. Распространение колебаний
2.2. Волна плоская, цилиндрическая, сферическая
2.3. Волны продольные и поперечные. Поляризация
Лекция 2
3.1. Возникновение волны. Группа волн
3.2. Точечный источник волн
3.3. Множество точечных источников
Лекция 3
3.4. Периодически расположенные точечные источники волн
3.5. “Точный” расчет углового распределения
потока энергии от системы источников
3.5.1. Непрерывное распределение источников
3.5.2. Излучение пары точечных источников
3.5.3. Излучение цепочки периодически
расположенных источников
Лекция 4
4. Законы геометрической оптики
4.1. Прямолинейность распространения света. Принцип Ферма
4.2. Отражение света. Плоское зеркало
4.3. Сложение гармонических колебаний
Лекция 5
4.4. Эллиптическое зеркало.
Уточненная формулировка принципа Ферма
4.5. Сферическое зеркало
4.6. Параболическое зеркало
4.7. Закон преломления света
4.7.1. Скорость света в веществе
Лекция 6
4.7.2. Преломление света
4.7.3. Дисперсия и поглощение света
4.7.4. Групповая и фазовая скорости света в веществе
4.7.5. Аномальная дисперсия
Лекция 7
5. Распространение (плоской) волны. Некоторые “тонкости”
6.1. Отражение света на границе раздела двух сред.
Угол Брюстера
6.2. Полное отражение
Лекция 8
7. Линза
7.1. Фокусные расстояние для сферической поверхности
7.2. Фокусное расстояние линзы
7.3. Фокусное расстояние линзы. Другой подход
7.4. Построение изображения предмета. Увеличение
Лекция 9
8. Интерференция
8.1. Двухлучевая интерференция. Точечные источники
8.2. Опыт Юнга. Когерентность волн
8.3. Длина когерентности
8.4. Линии равного наклона
Лекция 10
8.5. Линии равной толщины
8.6. Интерферометры
8.6.1. Интерферометр Линника
8.6.2. Интерферометр Рэлея
8.6.3. Звездный интерфероментр Майкельсона
8.6.4. Интерферометр Фабри-Перо
Лекция 11
8.6.5 Интерферометр Фабри-Перо.
Угловое распределение амплитуды проходящей волны
9. Дифракция Фраунгофера
9.1. Дифракция на щели
9.2. Дифракционная решетка
9.3. Дифракционная решетка как спектральный прибор
Лекция 12
10. Дифракция на круглом отверстии
10.1. Зоны Френеля
10.2. Обсуждение полученных результатов. Зонная пластинка
10.3. Линза как дифракционный прибор
10.4. Пятно Пуассона
Лекция 13
11.1. Свет поляризованный и неполяризованный. Закон Малюса
11.2. Одноосные кристаллы
11.3. Скрещенные поляризаторы
11.4. Двойное лучепреломление
11.5. Поляризаторы
Лекция 14
11.6. Анализ поляризованного света
11.7. Естественное вращенние плоскости поляризации
11.8. Эффект Зеемана и поляризация
11.9. Искусственное двойное лучепреломление
Лекция 15
12. Тепловое излучение
12.1. Основные понятия. Закон Кирхгофа
12.2. Плотность лучистой энергии
12.3. Лучистая энергия
12.4. Формула Планка
Лекция 16
12.5. Закон Стефана-Больцмана и закон Вина
12.7. Оптическая пирометрия
13.1. Теплоемкость кристаллической решетки
Лекция 17
13.2. Теплоемкость кристаллической решетки. Продолжение
14.1. Преобразования Лоренца
14.2. Эффект Допплера
14.3. Поперечный эфект Допплера. Аберрация
Лекция 18
15. Фотоны
16. Примеры использования понятия фотона
16.1. Опыт Боте
16.2. Энергетические соотношения
16.3. Эффект Комптона
Лекция 19
17. Гипотеза де Бройля
18.1. Дифракция электрона на двух щелях
18.2. Соотношения неопределенностей
18.3. Уравнение Шрёдингера
Лекция 20
18.4. Стоячая волна
18.5. Физический смысл волновой функции
19.1. Как нам это объясняют
Лекция 21
19.2. Как нам это понимать
19.3. Парадокс Больцмана
19.4. Химические элементы
19.5. Нормирование волновой функции
Лекция 22
20. Стоячие волны. Рефракция
21. “Внутреннее движение” квантового состояния
22. Квантование момента импульса
23. Классический гироскоп в магнитном поле
![]() Лекция 2 13
Лекция 2 13
Лекция 2
3.1. Возникновение волны. Группа волн





![]()
![]()
![]()
Пожалуй, самыми наглядными являются волны на поверхности воды. Их можно просто увидеть невооруженным взглядом. При каких условиях возникают такие волны? Проще всего бросить камень, скажем, в пруд со спокойной поверхностью воды. От места падения камня начнет распространяться волна, которую можно назвать кольцевой. Ее амплитуда в зависимости от расстояния до точки падения будет изменяться так же, как и у волны цилиндрической.
Однако, это не совсем такая волна, о которой мы говорили. Синусоидальная волна не должна иметь начала или конца, чего, конечно, нельзя сказать о волне, возникшей при падении камня в воду.
![]() x
x
0 r
![]()
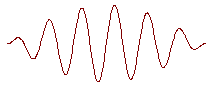
Совсем не обязательно, чтобы такая группа волн имела показанную на рисунке динамику увеличения и уменьшения амплитуды, показанный профиль. Для нас важнее понять, почему волна в этом случае имеет название “группы”. Для этого надо вспомнить возникновение биений, которые наблюдаются при сложении колебаний близких частот. Разность фаз таких колебаний
![]()
изменяется достаточно медленно. Между моментами, когда амплитуда суммарных колебаний
![]()
![]()
![]()
![]()
![]()
со средней
частотой ![]() обращается
в нуль, проходит
достаточно
много (по сравнению
с периодом
колебаний)
времени:
обращается
в нуль, проходит
достаточно
много (по сравнению
с периодом
колебаний)
времени:
![]() ;
;
![]() ;
;
![]() ,
,
поскольку
разность частот
колебаний много
меньше средней
частоты: ![]() .
Поэтому мы
наблюдаем
приблизительно
гармонические
колебания с
медленно изменяющейся
амплитудой.
Амплитудой
в этом случае
называется
произведение
подчеркнутых
сомножителей
в выписанных
выше выражениях.
.
Поэтому мы
наблюдаем
приблизительно
гармонические
колебания с
медленно изменяющейся
амплитудой.
Амплитудой
в этом случае
называется
произведение
подчеркнутых
сомножителей
в выписанных
выше выражениях.
Предположим теперь, что вдоль некоторого направления распространяются плоские волны с близкими длинами волн. Соответственно и частоты распространяющихся с ними колебаний будут близкими. В каждой точке, например, в точке x = 0 будут наблюдаться биения:
![]()
![]() .
.
С другой стороны, в фиксированный момент времени (пусть t = 0) мы получим такой профиль волны:
![]()
![]() .
.
В этом
выражении ![]() ,
k
- среднее значение
волнового
числа. Обратите
внимание на
сходство выражения,
описывающее
профиль нашей
волны, и выражения,
которое описывает
процесс биений.
,
k
- среднее значение
волнового
числа. Обратите
внимание на
сходство выражения,
описывающее
профиль нашей
волны, и выражения,
которое описывает
процесс биений.
Для произвольных значений времени и координаты мы получим такое выражение:
![]()
![]() .
.
В общем то, мы просто занимались некоторыми тригонометрическими преобразованиями. Но получили весьма любопытный и очень важный результат. Хотя его важность обнаружится еще нескоро.
Зададимся вновь вопросом: чему равна скорость распространения волны? Оказывается, ответ на этот вопрос неоднозначен. Для синусоидальной волны это скорость движения точки с постоянной фазой:
![]()
![]() .
.
Это так называемая фазовая скорость. Но предположим, мы хотим измерить скорость распространения волны. Вообще говоря, для этого создается некоторый импульс (группа волн, волновой пакет, цуг) и измеряется время прохождения им некоторого расстояния. Но тогда мы определим скорость волны как скорость перемещения не точки с постоянной фазой, а точки с постоянной амплитудой (подчеркнутая группа сомножителей в выписанном выражении):
![]() ;
;
![]() .
.
Посмотрим когда и почему эти скорости оказываются различными.
Продифференцируем фазовую скорость, например, по волновому числу k:
![]() .
.
![]() x
x
0 X
![]()
![]()
Волновые пакеты при распространении
двух синусоидальных волн с близкими
частотами (длинами волн).

![]()
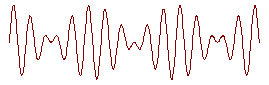
Собственно, при гидролокации, радиолокации и проч. мы имеем дело именно с групповой скоростью, мы измеряем именно групповую, а не фазовую скорость, так что это очень важное понятие.
Подведем некоторый итог этой части разговора о волнах. Если наблюдается сумма колебаний различных частот, то обнаруживается изменение амплитуды во времени. Справедливо и обратное утверждение: если амплитуда колебаний непостоянна, значит мы имеем дело с суммой нескольких колебаний. Применительно к волне это означает, что при распространении некоторого волнового импульса мы наблюдаем распространение нескольких волн, некоторой их группы. Скорость распространения импульса потому и называется групповой. Количество синусоидальных волн, образующих импульс (волновой пакет, группу волн, цуг) может быть как конечным (минимум - две), так и бесконечным.
Заметим еще, что фазовая скорость может оказаться больше скорости света в вакууме, что невозможно для групповой скорости. При определенных условиях эти скорости вообще могут быть разного знака.
Похожие работы
... основ и ясно поставленных целей, обучение зачастую сводится к передаче знаний посредством бессистемных методов и приемов. Перестройка школы, совершенствование учебно-воспитательного процесса требуют от учителя особое внимание уделять развитию критического мышления учащихся. [3] 1.3 Физика как основа для развития критического мышления Безусловно, этот процесс должен быть комплексным, т.е. ...
... приборы (рычажные весы, электроскоп и др.); -работы, выполняемые на приборах, выпускаемых промышленностью. Классификация взята из [1]. В своей книге [2] С.Ф. Покровский показал, что домашние опыты и наблюдения по физике, проводимые самими учащимися: 1)дают возможность нашей школе расширить область связи теории с практикой; 2)развивают у учащихся интерес к физике и технике; 3)будят ...
... пользователя: VI—XI классы. Платформа: Windows. Носитель: компакт-диск. Варианты построения уроков с использованием электронного учебника 1. Электронный учебник используется при изучении нового материала и его закреплении (20 мин. работы за компьютером). Учащихся сначала опрашивают по традиционной методике или с помощью печатных текстов. При переходе к изучению нового материала ...
... значениями этих параметров, чтобы определить предельные значения и шаг расчёта рассчитываемых параметров. Заключение Хочется выразить уверенность, что в следующих версиях курса "Открытая физика" количество компьютерных моделей будет расти, их функциональные возможности станут разнообразнее, а пределы изменения числовых значений параметров, описывающих эксперименты, будут расширены. Надеемся, что ...


0 комментариев