Навигация
Ошибка выборки
2. Ошибка выборки.
Возникает из-за различий в вариации значений изучаемого признака у единиц выборочной и генеральной совокупности. Поскольку при соблюдении требований случайного отбора все единицы генеральной совокупности имеют равные шансы попасть в выборку, состав выборки может значительно изменяться при повторении испытаний. Соответственно будут меняться параметры выборки, и возникать ошибки выборки. Ошибки выборки неизбежны, они вытекают из сути метода. Ошибки выборки не могут быть постоянными при повторении отбора.
Ошибка выборки в статистике это некоторая средняя величина или обобщающая характеристика, ошибок полученных при многократном повторении испытаний.
W - P
- ошибка выборки;
- выборочная средняя;
- генеральная средняя;
W – доля единиц, обладающих изучаемым признаком в выборочной совокупности (выборочная доля);
P - доля единиц, обладающих изучаемым признаком в генеральной совокупности.
Величина ошибок зависит от способа отбора. В математической статистике доказано, что средняя ошибка выборки (математическое ожидание средней ошибки выборки) – это среднеквадратическое отклонение распределения выборочной средней величины.
Ошибка выборки определяется:
В математической статистике доказано, что средняя ошибка собственно случайного повторного отбор рассчитывается: , где
- средняя ошибка выборки;
- дисперсия генеральной совокупности;
- численность выборки.
Если исследуется выборочная доля при повторном отборе , где - дисперсия биномиального распределения.
Результаты повторного отбора подчиняются закону биномиального распределения.
При бесповторном отборе результаты многократной выборки и распределения ошибок подчиняются гипергеометрическому распределению, и формула средней ошибки имеет вид: , соответственно для выборочной доли .
При выборках большой численности, когда из массовых генеральных совокупностей () для расчета ошибок выборки можно использовать формулу повторного отбора.
В формулах средней ошибки выборки присутствует генеральная дисперсия. Однако, она, как правило, неизвестна. Если мы проводим выборку для того, чтобы изучить только часть совокупности, мы не можем знать генеральную дисперсию. Исключение составляют только выборки, проводимые для контроля результата сплошного наблюдения.
Однако, математической статистикой доказано, что если выборка производится из нормального распределения совокупности генеральная и выборочная дисперсия связаны между собой следующим образом:
| |
| ||||
Из формулы видно, что достаточно большой выборке (n-1)®n, а , откуда s2» S2. Поэтому для расчета средних ошибок выборки на практике используют выборочные дисперсии.
| | | ||||
Если многократно проводить выборки из одной и той же генеральной совокупности, то конкретному размеру ошибки выборки будет соответствовать та или иная статистическая вероятность ее появления.
Вероятности конкретного размера ошибок подсчитать невозможно (нецелесообразно), гораздо важнее знать, что ошибка наблюдений не выйдет за определенные пределы.
|
| |
t=1, 2, 3
По формуле Чебышева, если
t=1 r³0
t=2 r³0,75
t=3 r³0,89
Эта формула для условий повторного отбора.
Академик Марков доказал, что предельная теорема справедлива и для бесповторного отбора.
Академик Ляпунов доказал, что вероятности предельных ошибок многочисленных выборок подчиняются закону нормального распределения, следовательно, для определения вероятностей нахождения ошибки выборки в заданных пределах можно использовать интегральную формулу Лапласа.
Площадь кривой ±s 0,6827
2s 0,9545
3s 0,9973
Отсюда, если доверительный коэффициент t=1, то вероятность того, что предельная ошибка выборки не будет больше, чем средняя ошибка, которая составляет 0,683.
Вероятный интервал изменения генеральной средней или доли в статистике принято называть доверительным интервалом.
Пример: Для анализа жирности молока из партии в 1000 фляг было отобрано и проверено 30. Средний процент жирности в проверенных флягах составил 3,51%, при среднеквадратическом отклонении 0,35. С вероятностью 0,954 определить доверительный интервал средней жирности партии молока (если выборка бесповторная).
| |
n=30
=3,51%
S=0,35%
Если мы расширим допустимые пределы точности, то вероятностная надежность результата будет выше, а точность ниже.
Если p=0,997 то t=3, а D=0,19 тогда ожидаемая жирность молока в генеральной совокупности должна составить .
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... распределения генеральной совокупности F(x) и – эмпирической функция распределения Fn(x) , построенной по выборке х1,…,хn, называется функция. Теорема. Если F(x) непрерывна, то распределения статистики Колмогорова Dn не зависит от F(x). Условные математические ожидания и условные распределения. Св-ва условных мат. ожиданий. Аналоги формул полной вероятности и формулы Байеса для мат. ожиданий ГММЕ ...
... дает возможность статистического моделирования, происходящих в населении процессов. Потребность в моделировании возникает в случае невозможности исследования самого объекта. Наибольшее число моделей, применяемых в статистике населения, разработано для характеристики его динамики. Среди них выделяются экспоненциальные и логистические. Особое значение в прогнозе населения на будущие периоды имеют ...
... на задний план традиционными постановками. Несколько лет назад при описании современного этапа развития статистических методов нами были выделены [29] пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять "точек роста": непараметрика, робастность, бутстреп, интервальная статистика, статистика объектов нечисловой природы. Обсудим их. 5. ...
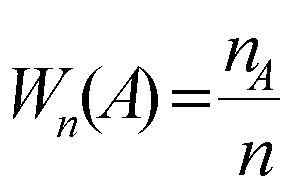
0 комментариев