Мазмұны
Кіріспе................................................................................................................3
1.1.Макро жүйелерге тән ерекшеліктер..........................................................5
1.2.Статистикалық таралу................................................................................7
1.3.Динамикалық шамалардың орта мәндерін есептеу................................11
1.4. Лиувилль теоремасы.................................................................................16
1.5. Статистикалық жүйенің энергиясы. Гиббстің микроканондық таралуы..............................................................................................................19
1.6. Кванттық жүйелердің ерекшеліктері.......................................................22
Қорытынды:
Пайдаланылған әдебиеттер:
Кіріспе
Мен "Статистикалық физиканың негіздері" тақырыбына курстық жұмыс жаздым. Бұл курстық жұмыста "Статистикалық таралу" , "Макро жүйелерге тән ерекшеліктер" , "Динамикалық шамалардың орта мәндерін есептеу" , "Лиувилль теоремасы" , "Статистикалық жүйенің энергиясы. Гиббстің микроканондық таралуы"Кванттық жүйелердің ерекшеліктері" тақырыптырна тоқталып өттім.
Кез келген макро дене өте көп атомдар мен молекулалардан және олар өзара өте күрделі заңдылықпен әсерлеседі.Бізді Қоршаан ортадаы макро денлердің және олардың бөліктерінің өзара әсерлесуінде тек электромагнитті күштерді ескеру жеткілікті.Себебі олардың арсындағы гравитациялық әсерлесу,шектен тыс аз болғандықтан ескеруге тұрмайды.Ал ядролық әсерлесулер ![]() см аралықта ғана, ядроның көлемінде білінетіндіктен және ядролар бөлінбейді деп есептесек,ядролық күштерді де ескермеуге болады.Сонымен, макро денелердің күйін электромагниттік күштер ғана анықтайды.Ал ол күштердің табиғаты классикалық электродинамикада жеткілікті зерттелген.
см аралықта ғана, ядроның көлемінде білінетіндіктен және ядролар бөлінбейді деп есептесек,ядролық күштерді де ескермеуге болады.Сонымен, макро денелердің күйін электромагниттік күштер ғана анықтайды.Ал ол күштердің табиғаты классикалық электродинамикада жеткілікті зерттелген.
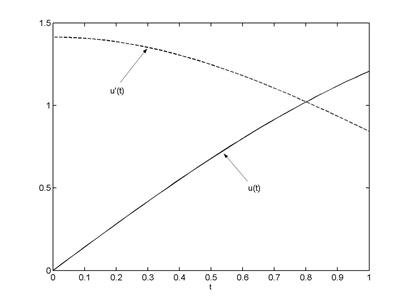
Фазалық кеңістік ұғымын жете түсіну үшін, бір еркіндік дәрежесі бар жүйе қарастырайық. Яғни кеңістіктегі Х осінің бойымен қозғалатын,массасы m бір бөлшекті алайық.Ондай жүйенің фазалық кеңістігі екі өлшемді (q,p) жазықтығы болады.Егер әрбір уақыт сәтіндегі координата мен импульстің уақытқа байланысты функциясы q(t),p(t) белгілі болса,олар фазалық жазықтықтағы траекторияның параметрлік теңдеуі болып табылады.Егер олардағы уақытты шығарып тастасақ,p=p(q) теңдеуі фазалық траекторияның канондық теңдеуін береді.
Лиувилль теоремасы бойынша, тепе – теңдіктегі жүйе үшін ықтималдық тығыздығы функциясы сақталу үшін, (1.20) Пуассон жақшасы нөлге тең болуы керек.Басқаша айтқанда, тұйық жүйенің таралу функциясы, сақталатын шамаларға ғана тәуелді болу керек. Механикада сақталатын негізгі инварианттар – жүйенің импульсі, импульс моменті және энергиясы екендігі белгілі.Бұлар,барлығы жеті қозғалыс интегралдарын береді.Таралу функциясы жалпылауыш координаталар мен импульске тікелей байланысты емес, қозғалыс интегралдары арқылы тәуелді болады.Таралу функциясы қозғалыс интегралдарына ғана байланысты болса, оның өзі де инвариантты шама болады.
Көп бөлшектен тұратын жүйенің статистикалық сипатын кванттық тұрғыдан зерттеу үшін оның құрамындағы бөлшектердің кванттық қасиеттері ескерілу керек.Көп бөлшектен тұратын жүйе ,үшін Шредингер теңдеуін шешу, қозғалыс теңдеулерін интегралдауға қарағанда, әлдеқайда күрделі. Тіпті Шредингер теңдеуін, қандай да бір жолмен шешкен күннің өзінде, оның белгілі бір шарттарды қанағаттандыратын толқындық функциясын жазу және одан пайдалы информация алу мүмкін емес.
Тығыздық матрицасы,немесе статистикалық матрица,кванттық статистикада таралу функциясының орнына жүреді.Өткен тақырыптарда көрсетілгендей,классикалық таралу функциясы жүйенің күйін қаншалықты дәл сипаттайтын болса,статистикалық матрица туралы да соны айтуға болады.Классикалық таралу функциясы p(q,p) ,жүйедегі бөлшектердің жалпылауыш координаталары мен импульстерінің берілген,нақты мәндерге ие болуының ықтималдығын көрсетсе,кванттық статистикадағы,![]() - жүйенің берілген кванттық күйде болу ықтималдығын көрсетеді.
- жүйенің берілген кванттық күйде болу ықтималдығын көрсетеді.
1.1.Статистикалық физиканың негізі
Макро жүйелерге тән ерекшеліктер
Классикалық механика бойынша,егер бөлшектерге әсер ететін сыртқы күштер мен олардың өзара әсерлесу заңдылықтары белгілі болса,онда дифференциялдық түрде жазылған қозғалыс теңдеулерін шешу арқылы берілген жүйенің ке келген уақыттағы күйін анықтауға болады дейміз.Ол үшін бөлшектердің бастапқы кездегі орындарымен олардың импульстері белгілі болу керек.Бірақ іс жүзінде бұл әдіс бойынша екі бөлшектен аспайтын жүйенің ғана күйңн дәл анықтауға болады.Ал өзара әсерлесетін бөлшектер саны үш немесе одан көп болған жағдайда берілген жүйенің қозғалыс теңдеулері дәл шешілмейді.
Кез келген макро денедегі атомдардың саны ![]() шамасында болады. Бұл өте үлкен сан.Мысалы, Қалыпты жағдайда 1
шамасында болады. Бұл өте үлкен сан.Мысалы, Қалыпты жағдайда 1![]() көлемдегі ауадағы молекулалардың шамамен
көлемдегі ауадағы молекулалардың шамамен ![]() болады.Егер осы молекулаларды әр секунд сайын бір милионнан шығарып отырсақ,оларды түгел шығару үшін 840 мың жыл қажет болар еді.Міне осындай орасан көп молекулалардың өзара әсерлесу заңдылығын анықтау мүмкін еместігі түсінікті. Жеке бөлшектердің өзара әсерлесу заңдылығы қаншалықты дәл анықталмағанмен, бөлшек саны өте көп болған жағдайда,олардың әсерлесуі,сапа жағынан мүлде жаңа сипатқа ие болады.Бұл жағдайда, классикалық тұрғыдан мүлде түсіндіруге түсіндіруге болмайтын,температура,энтропия деген сияқты,жаңа,ұжымдық түсініктерпайда болады.Мұндай күрделі жүйелердің көптеген қасиеттері мен құпияларын әлі күнге дейін толық біле алғымыз жоқ.Мысалы белгілі бір атомдар тобы, белгілі бір тәртіппен орналасып,тіршілік иесіне ғана тән,биологиялық объектінің кірпіші болып табылатын,клетка құрайды.Ондай клеткалар өзін-өзі жасау арқылы көбейе алады.Бұны материяның өзін-өзі ұйымдастыруы дейді.
болады.Егер осы молекулаларды әр секунд сайын бір милионнан шығарып отырсақ,оларды түгел шығару үшін 840 мың жыл қажет болар еді.Міне осындай орасан көп молекулалардың өзара әсерлесу заңдылығын анықтау мүмкін еместігі түсінікті. Жеке бөлшектердің өзара әсерлесу заңдылығы қаншалықты дәл анықталмағанмен, бөлшек саны өте көп болған жағдайда,олардың әсерлесуі,сапа жағынан мүлде жаңа сипатқа ие болады.Бұл жағдайда, классикалық тұрғыдан мүлде түсіндіруге түсіндіруге болмайтын,температура,энтропия деген сияқты,жаңа,ұжымдық түсініктерпайда болады.Мұндай күрделі жүйелердің көптеген қасиеттері мен құпияларын әлі күнге дейін толық біле алғымыз жоқ.Мысалы белгілі бір атомдар тобы, белгілі бір тәртіппен орналасып,тіршілік иесіне ғана тән,биологиялық объектінің кірпіші болып табылатын,клетка құрайды.Ондай клеткалар өзін-өзі жасау арқылы көбейе алады.Бұны материяның өзін-өзі ұйымдастыруы дейді.
Әлемдегі материяның өзін-өзі ұйымдастыруы, олардың өмір сүруінің жаңа формасын тудыруға әкеліп соғады.Бұл өз кезегінде,олардың арасындағы әсерлесу заңдылығын жаңа деңгейге,бұрынғыдан әлдеқайда күрделі,жоғары деңгейге көтереді.Осылайша материяның дамуының ең жоғары деңгейі,ұйымдасқан тіршілік иесін тудырады,және ең жоғары сатыда дамыған сана иесінің пайда болуына әкеледі.Әрине біз барлық даму сатысын зерттеп білдік дей аламыз.Бұл тұрғыдан алғанда біздің білетініміз өте аз. Материяның өзін-өзі ұйымдастыруын зерттеу,кейінгі кезде ғана қолға алына бастаған,жаңа ғылым саласы болып табылады.Біз бұл жерде табиғат заңдылығының өте күрделі екендігін көрсету үшін,мысал ретінде келтірдік.
Айналаны қоршаған өлі табиғаттағы макро денелер соншалықты жоғары дәрежеде ұйымдасқан деуге болмайды.Сондықтан олардың әсерлесу заңдылығы мен күйлерін зерттеп білуге болады.Бірақ,ол үшін жоғарыда айтылған классикалық механика әдісі жарамайтыны түсінікті.
Макро денелердің өзара әсерлесу заңдылығы,олардың құрамды бөліктері болып табылатын микро бөлшектердің әсерлесу заңдарына байланысты.Ал микро дүние үшін кванттық механиканың іргелі заңдары жұмыс істейді.Кванттық механика заңдарына сүйене отырып,көп бөлшектерден тұратын жұйелердің ұжымдық қасиеттерін анықтай аламыз.Бірақ,көп бөлшектер үшін Шредингер теңдеулерін шешу,Ньютондық механика бойынша қозғалыс теңдеулерін шешуден оңай емес.Олай болса,күрделі жүйелердің күйлерін анықтау үшін,бқл айтылған әдістерді тікелей қолдануға болмайды.Бірақ,күрделі жүйелердің күйлері,олардың ұүрамындағы бөлшектердің қозғалысын классикалық,немесе кванттық механика заңдары арқылы сипаттауға байланысты болмайды.Олай болса,қандай да бір механика заңдарына сүйене отырып,жүйенің берілген күйлерде болу ықтималдықтарын анықтауға болады.Бұл әдіс – статистикалық физканың негізі болып табылады.
Берілген жүйе классикалық механика заңдарына бағынады дейік.Жүйенің еркіндік дәрежесі s болсын.(Мысалы,өзара әсерлеспейтін,N бөлшектен тұратын жүйенің еркіндік дәрежесі 3N болады).Әрбір еркіндік дәрежесі үшін жазылған s дифференциялдық теңдеулер жүйесін шешу арқылы берілген жүйенің күйін анықтауға болар еді.Бірқ,бір-бірімен байланысқан,сонша көп теңдеулер жүйесін интегралдау мүмкін емес.Тіпті,қандай да бір жолын тауып,ол теңдеулерді шешкен күннің өзінде,сонша көп информацияны талдап,пайдалану мүмкін болмас еді.Дифференциалдық теңдеулерді интегралдау үшін бастапқы шарттар қажет,яғни жүйедегі әрбір бөлшектің алғашқы кездегі орындары мен импульстері белгілі болу керек.Осыншама көп бастапқы шарттарды пайдалану мүмкін емес. Осы айтылған қиындықтарға қарап,макро жүйелердің күйін анықтау,олардың заңдылықтарын білу мүмкін емес сияқты көрінеді.Дегенмен,бөлшектер саны көбейген сайын,жүйенің кейбір қасиеттері айқындала түсетінін көреміз.Мұндай қасиеттерін жүйенің статистикалық заңдылықтарымен байланыстырамыз.Мысалы дененің температурасы- оның статистикалық қасиеті.Бөлшек сандары азайған сайын статистикалық қасиеті жойыла бастайды.Бірнеше молекуланың температурасы деген түсінік болмайды.Олай болса,Бөлшек саны аз кезде біліне бермейтін,тек өте көп бөлшектер жиынтығына ғана тән,жаңа қасиеттер пайда болады.Статистикалық физиканың негізгі мәселесі,макро денелерге ғана тән,статистикалық заңдылықтарды анықтау болып табылады.
1.2.Статистикалық таралу
Классикалық статистиканың негізгі мәселелерін талқыламас бұрын,фазалық кеңістік ұғымын енгізу қажет. Механикалық жүйенің күйі,оның құрамындағы бөлшектердің координаталары мен импульстері арқылы анықталады.Егер жүйенің s еркіндік дәрежесі болса,әрбір еркіндік дәрежеге сәйкес,s координаталар жиыны берілу кере.Оларды жүйенің жалпылауыш координаталары дейміз және ![]() деп белгілейік.Жалпылауыш координаталардан уақыт бойынша алынған туынды,сол еркіндік дәрежеге сәйкес,жылдамдық болып табылады.Статистикада жүйенің күйін жалпылауыш координаталармен бірге жалпылауыш импульстер арқылы көрсету де қажет болады.Оларды тиісінше,
деп белгілейік.Жалпылауыш координаталардан уақыт бойынша алынған туынды,сол еркіндік дәрежеге сәйкес,жылдамдық болып табылады.Статистикада жүйенің күйін жалпылауыш координаталармен бірге жалпылауыш импульстер арқылы көрсету де қажет болады.Оларды тиісінше, ![]() деп белгілейік.Жалпылауыш координаталармен импульстерді біріктіретін,барлығы 2s айнымалыдан тұратын кеңістікті – фазалық кеңістік деп атайды.Фазалық кеңістікті (
деп белгілейік.Жалпылауыш координаталармен импульстерді біріктіретін,барлығы 2s айнымалыдан тұратын кеңістікті – фазалық кеңістік деп атайды.Фазалық кеңістікті (![]() ) түрінде жазуға болады.Мұндағы i=1,2,…s еркіндік дәрежелерін кқрсетеді.Әрине фазалық кеңістік шын кеңістік емес,математикалық абтракция екенін естен шығармау керек.Жүйенің әр түрлі күйлеріне фазалық кеңістіктегі әр түрлі нүктелер әйкес келеді,және керісінше әрбір нүкте жүйенің белгілі бір күйін білдіреді.Әр түрлі макро жүйелерге әр түрлі фазалық кеңістік сәйкес келеді.Оның өлшемі,жүйенің екі еселенген еркіндік дәрежесінің санына тең.Координаталар мен импульстердің белгілі бір жиынтығы фазалық кеңістіктегі бір нүктені көрсетеді.Жүйенің құрамындағы бөлшектердің координаталары мен импульстері үздіксіз өзгерісте болатындықтан,фазалық кеңістіктегі жүйенің күйін сипаттайтын нүкте де үздіксіз қозғалыста болады.Яғни жүйенің
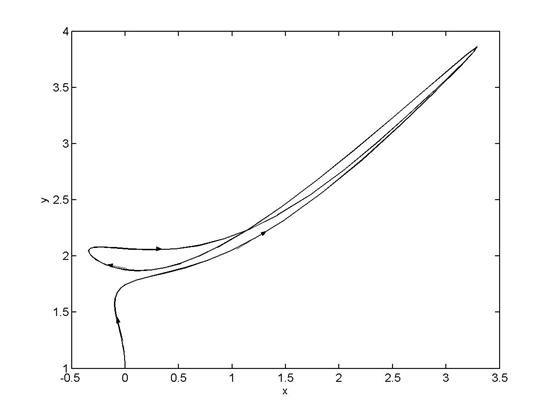
) түрінде жазуға болады.Мұндағы i=1,2,…s еркіндік дәрежелерін кқрсетеді.Әрине фазалық кеңістік шын кеңістік емес,математикалық абтракция екенін естен шығармау керек.Жүйенің әр түрлі күйлеріне фазалық кеңістіктегі әр түрлі нүктелер әйкес келеді,және керісінше әрбір нүкте жүйенің белгілі бір күйін білдіреді.Әр түрлі макро жүйелерге әр түрлі фазалық кеңістік сәйкес келеді.Оның өлшемі,жүйенің екі еселенген еркіндік дәрежесінің санына тең.Координаталар мен импульстердің белгілі бір жиынтығы фазалық кеңістіктегі бір нүктені көрсетеді.Жүйенің құрамындағы бөлшектердің координаталары мен импульстері үздіксіз өзгерісте болатындықтан,фазалық кеңістіктегі жүйенің күйін сипаттайтын нүкте де үздіксіз қозғалыста болады.Яғни жүйенің ![]() фазалық кеңістікте белгілі бір траекториямен жылжып отырады.Ондай сызықты – фазалық траектория деп атаймыз.Әрине, фазалық кеңістіктегі траектория мен, жүйенің реал кеңістіктегі траекториясын шатастыруға болмайды.
фазалық кеңістікте белгілі бір траекториямен жылжып отырады.Ондай сызықты – фазалық траектория деп атаймыз.Әрине, фазалық кеңістіктегі траектория мен, жүйенің реал кеңістіктегі траекториясын шатастыруға болмайды.
Нақты болу үшін,Х осінің бас нүктесінің төңірегінде тербеліп тұрған гармониялық осцилляторды қарастырайық.Оның қозғалыс теңдеуін мына түрде жазуға болады:
m![]() =-kq,немесе
=-kq,немесе ![]() q=0;мұндағы w=
q=0;мұндағы w=![]()
Бұл теңдеудің жалпы шешімін мына түрде жазамыз:q=![]() sin(ωt+α).
sin(ωt+α).
Координатадан уақыт бойынша туынды алып,материалдық нүктенің жылдамдығын және импульсін анықтай аламыз.Сонда фазалық траекторияның параметрдік теңдеуін мына түрде жазамыз:
q=![]() sin(ωt+α); p=mω
sin(ωt+α); p=mω![]() cos(ωt+α);
cos(ωt+α);
Бұл теңдеулер жүйесін уақытты шығарып тастап,траекторияның канондық теңдеуін аламыз:
![]() +
+![]() =1;
=1;
Бұл теңдеу,жарты осьтері q=![]() p=mω
p=mω![]() болатын эллипстің теңдеуі.Бұл жердегі
болатын эллипстің теңдеуі.Бұл жердегі ![]() - тербеліс амплитудасы, mω
- тербеліс амплитудасы, mω![]() импульстің максимал шамасы.Осциллятордың кез келген уақыттағы күйін осы эллипс сызығының үстінен көрсетуге болады.
импульстің максимал шамасы.Осциллятордың кез келген уақыттағы күйін осы эллипс сызығының үстінен көрсетуге болады.
Классикалық механика бойынша,материалдық нүктенің координата мен импульсін бір мезгілде дәл көрсетуге болады.Ол күйге фазалық кеңістіктегі нүкте сәйкес келеді.Сондықтан,классикалық бөлшектің фазалық кеңістіктегі траекториясын жіңішке сызық деп есептеуге болады.Ал кванттық бөлшек үшін координата мен импульсті бір мезгілде дәл көрсете алмаймыз.Олай болса,кванттық бөлшектің күйін фазалық кеңістіктегі нүкте арқылы көрсетуге болмайды.Бір еркіндік дәрежесі бар жүйе үшін координата мен импульс арасындағы анықталмағандық өатынас ![]() болады.Жоғарыда қарастырған осциллятор күйін,эллипс сызығының үстінде жатқан,ауданы
болады.Жоғарыда қарастырған осциллятор күйін,эллипс сызығының үстінде жатқан,ауданы ![]() - Планк тұрақтысынан кем болмайтын,кішкене ұя арқылы көрсету керек.
- Планк тұрақтысынан кем болмайтын,кішкене ұя арқылы көрсету керек.
Алдағы тақырыптарда фазалық кеңістіктің көлемі деген ұғымды пайдалануға тура келеді.Егер көп бөлшектерден тұратын жүйенің әрбір еркіндік дәрежесіне сәйкес координатасы мен импульсі ![]() ,
,![]() аралығында жататын болса,онда жүйенің фазалық кеңістіктегі күйі
аралығында жататын болса,онда жүйенің фазалық кеңістіктегі күйі
![]() ,
,![]() (1.1)
(1.1)
кішкене көлем ішінде жатады дейміз.Фазалық кеңістіктің жалпылауыш координаталарға сәйкес бөлігін – конфигурациялық кеңістік,ал импульстерге сәйкес бөлігін – импульстік кеңістік деп атайды.Оларға сәйкес кеңістіктердің көлемдерін бөлек есептеуге болады:
![]() =
=![]() ,
,![]()
![]() =
=![]() ;
;
Классикалық механика да, кванттық механика да көп бөлшектен тұратын жүйенің фазалық кеңістіктегі күйін дәл анықтай алмады.Сондықтан,осы жерден бастап,статистикалық әдісті қолдануға тура келеді.статистикалық әдіс бойынша жүйенің күйінің фазалық кеңістіктегі,кішкене dГ көлем ішінде жатуының ықтималдығын көрсетуге болады дейміз.Ол ықтималдықтың шамасы,сол dГ көлемге пропорционал болатындығы түсінікті.
Dω=p(![]() )
)![]() dГ (1.2)
dГ (1.2)
Бұл жердегі p(![]() ) – фазалық кеңістіктегі ықтималдықтың тығыздығы деп аталады.Ықтималдық тығыздығы,берілген dГ көлемді фазалық кеңістіктің қай бөлігінен таңдап алғанымызға ,яғни жалпылауыш координаталар мен импульстерге байланысты болады.Алдағы жерде жазуды жеңілдету үшін,жалпылауыш координаталар жиынын бір ғана q әрпімен,ал жалпылауыш импульстер жиынын p әрпімен белгілеуге келісейік.Сонда, статистикалық таралу функциясы деп аталатын,фазалық кеңістіктегі ықтималдық таралу функциясын p(q,p) түрінде жазамыз.Бұл функция белгілі нормалау шартын қанағаттандыру керек.
) – фазалық кеңістіктегі ықтималдықтың тығыздығы деп аталады.Ықтималдық тығыздығы,берілген dГ көлемді фазалық кеңістіктің қай бөлігінен таңдап алғанымызға ,яғни жалпылауыш координаталар мен импульстерге байланысты болады.Алдағы жерде жазуды жеңілдету үшін,жалпылауыш координаталар жиынын бір ғана q әрпімен,ал жалпылауыш импульстер жиынын p әрпімен белгілеуге келісейік.Сонда, статистикалық таралу функциясы деп аталатын,фазалық кеңістіктегі ықтималдық таралу функциясын p(q,p) түрінде жазамыз.Бұл функция белгілі нормалау шартын қанағаттандыру керек.
![]() dq
dq![]() dp
dp![]() 1 (1.3)
1 (1.3)
Яғни,жүйенің күйінің фазалық кеңістік ішінде жатуының толық ықтималдығы бірге тең болады.Бұл жердегі интеграл барлық фазалық кеңістік бойынша алынады және dq – конфигурациялық,ал dp - импульстік кеңістікті білдіреді.
Жүйенің берілген dГ=dq![]() dp көлем ішінде болу ықтималдығын анықтау үшін,жүйені ұзақ T уақыт
dp көлем ішінде болу ықтималдығын анықтау үшін,жүйені ұзақ T уақыт ![]() бақылайық
бақылайық ![]() .Жүйе сол уақыттың
.Жүйе сол уақыттың ![]() бөлігін берілген dГ көлем ішінде өткізейік дейік.Бұл жердегі
бөлігін берілген dГ көлем ішінде өткізейік дейік.Бұл жердегі ![]() бақылау
бақылау![]() - абстракциялық мағынада айтылып отыр.Жүйенің күйін шын бақылау мүмкін емес.Егер бақылау уақытын шексіз ұзартсақ, аталған ықтималдық былай анықталады:
- абстракциялық мағынада айтылып отыр.Жүйенің күйін шын бақылау мүмкін емес.Егер бақылау уақытын шексіз ұзартсақ, аталған ықтималдық былай анықталады:
ω=![]() (1.4)
(1.4)
Фазалық кеңістіктегі траектория өте күрделі және шатасқан болғандықтан, жүйенің күйі берілген көлем ішінде бірнеше қайтара кіріп және шығып жатуы мүмкін.Сондықтан ![]() бірнеше бөліктерден тұратын уақыттардың қосындысы болады.
бірнеше бөліктерден тұратын уақыттардың қосындысы болады.
Классикалық механикадағы себептілік принципі бойынша,егер жүенің бөлшектерінің алғашқы кездегі орындары мен жылдамдықтары белгілі болса және оларға әсер ететін барлық күштер берілсе,онда жүйенің болашақтағы кез келген уақыт сәтіндегі күйін бір мәнді анықтауға болады дейді.Бұны классикалық детерменизм принципідеп атайды.Бір сөзбен айтқанда, кез келген күрделі жүйенің күйі,оның алғашқы кездегі күйіне байланысты болу керек.Бұл принцип,механиканың заңдарының уақыттың таңбасын өзгертуге қарағанда инвариантты болуынан туындайды.Кез келген механикалық процесс қайтымды болады.Бірақ бұл принциптің көп бұлшектерден тұратын жүйелер үшін орындалмайтыны белгілі.Жүйенің фазалық кеңістіктегі траекториясы соншалықты күрделі және шатасып жатады.Сондықтан бөлшектер өзара бірнеше соқтығысулардан кейін, жүйенің алғашқы кездегі қандай күйде болғандығы мүде қажетсіз болып қалады.
Макро дене,немесе денелер жүйесі берілсін.Бұл жүйе тұйықталған болсын,яғни оған сырттан ешқандай денелер,немесе өрістер әсер етпейді дейік.Тұйықталған жүйені өзіне өзін беріп қойсақ біраз уақыттан кейін тепе-теңдік күйге келетіні белгілі.Тепе-теңдікті тұрған тұйық жүйенің ішіндегі әсерлесулер ол жүйені тепе-теңдік қалыптан шығара алмайды.Тепе-теңдікте тұрған тұйық жүйенің кішкене бұлігін қарастырайық.Өз кезегінде бұл кішкене бөліктің ішіндегі бөлшектер саны өте көп болсын.Жүйенің мұндай бөлігі үшін статистика заңдарын қолдануға болатын болса,оның ![]() кішкене жүйе
кішкене жүйе![]() ,немесе негізгі жүйенің бөлігі деп атаймыз.Таңдап алынған кішкене жүйені тұйық деп айта алмаймыз,ол негізгі жүйенің бөлшектерімен күрделі әсерлеседі.Алғашқы кезде кішкене жүйенің бөлшектерінің орындары мен жылдамдықтары белгілі болған дейік.Содан кейін кішкене жүйе,негізгі жүйенің бөлшектерімен әсерлесу нәтижесінде,өз күйін өзгертіп,негізгі жүйемен тепе-теңдікке келеді.Алғашқы кезде кішкене жүйе қандай күйде болса да,әсерлесу нәтижесінде,негізігі жүйемен бәрібір тепе-теңдікке келеді,яғни бастапқышарттың кішкене жүйе күйіне әсері болмайды.Бқл мысал,статистикалық жүйе күйін анықтау үшін механика заңдарының әлсіз екендігін көрсетеді.Кішкене жүйенің фазалық кеңістіктегі траекториясының күрделі болуы,оған механика заңдарын қолдануға кедергң келтіреді.Екінші жағынан,фазалық траекторияның күрделілігі,оған статистика заңын қолдануға мүмкіндік береді.
,немесе негізгі жүйенің бөлігі деп атаймыз.Таңдап алынған кішкене жүйені тұйық деп айта алмаймыз,ол негізгі жүйенің бөлшектерімен күрделі әсерлеседі.Алғашқы кезде кішкене жүйенің бөлшектерінің орындары мен жылдамдықтары белгілі болған дейік.Содан кейін кішкене жүйе,негізгі жүйенің бөлшектерімен әсерлесу нәтижесінде,өз күйін өзгертіп,негізгі жүйемен тепе-теңдікке келеді.Алғашқы кезде кішкене жүйе қандай күйде болса да,әсерлесу нәтижесінде,негізігі жүйемен бәрібір тепе-теңдікке келеді,яғни бастапқышарттың кішкене жүйе күйіне әсері болмайды.Бқл мысал,статистикалық жүйе күйін анықтау үшін механика заңдарының әлсіз екендігін көрсетеді.Кішкене жүйенің фазалық кеңістіктегі траекториясының күрделі болуы,оған механика заңдарын қолдануға кедергң келтіреді.Екінші жағынан,фазалық траекторияның күрделілігі,оған статистика заңын қолдануға мүмкіндік береді.
Кішкене жүйеге,оны қоршаған үлкен жүйе тарапынан әсер етуші күштердің күрделі болуы,ұзақ уақыт бақылау кезінде,кішкене жүйе Күйлерінің,фазалық кеңістікте берілген dГ көлем ішіндегі барлық нүктелерде жеткілікті уақыт болуына көмектеседі.Себебі, фазалық траектория соншалықты шатасқан болғандықтан,берілген көлемдітолық толтыруға тырысады дейміз.Олай болса,берілген dГ көлем ішінде қанша уақыт болғанын ![]() есептеп
есептеп![]() ,(1.4) бойынша іздеп отырған ықтималдықты анықтауға болар еді.Әрине,іс жүзінде ықтималдықты анықтаудың басқа,анағұрлым жеңіл жолын іздеу керек.Міне бұл проблема – статистикалық физиканың негізгі мәселесі болып саналады.
,(1.4) бойынша іздеп отырған ықтималдықты анықтауға болар еді.Әрине,іс жүзінде ықтималдықты анықтаудың басқа,анағұрлым жеңіл жолын іздеу керек.Міне бұл проблема – статистикалық физиканың негізгі мәселесі болып саналады.
1.3.Динамикалық шамалардың орта мәндерін есептеу
Егер берілген жүйе үшін статистикалық таралу функциясы белгілі болса,онда сол жүйенің күйін сипаттайтын кез келген физикалық шамаларды ңорта мәндерін есептеуге болады.Жүйенің жалпылауыш координаталары мен жалпылауыш импульстеріне тәуелді физикалық шамалар,сол жүйені сипаттайтын динамикалық шамалар болып табылады.Тепе-теңдікте тұрған жүйе үшін f(q,p) физикалық шамасының орта мәнін анықтайық.Ол үшін оның мүмкін болатын мәндерін,жүйенің фазалық кеңістіктегі (q,p) күйде болу ықтималдығына көбейтіп,барлық фазалық кеңістік бойынша интеграл алу керек.
![]() (q,p)
(q,p)![]() p(q,p)dq
p(q,p)dq![]() dp (1.5)
dp (1.5)
Бұл формула,динамикалық шамаларды статистикалық орталауды көрсетеді.Ықтималдық тығыздығының таралу функциясы бойынша орталау,динамикалық шаманың шын мәнінің уақыт бойынша өзгеруін бақылауды қажет етпейді. Динамикалық шама уақыттың күрделі функциясы болып табылады. Себебі, f(q,p) функциясындағы (q,p) айнымалылары уақытқа тәуелді. (1.5) интегралын есептеп,оның шектерін қойған соң шыққан шама (q,p) айнымалыларына тәуелді болмайтындықтан, (1.5) бойынша еептелген орта мен уақытқа байланысты емес,тұрақты шама болады.
Егер берілген динамикалық шаманың мәнінің өзгерісін ұзақ уақыт бойы қадағалап отырып, (1.4) формуласына сәйкес,уақыт бойынша орталасақ,берілген шаманың орта мәні анықталар еді.
![]() (1.6)
(1.6)
(1.4)ықтималдықтың анықтамасы бойынша,(1.5) және (1.6) формулалары арқылы анықталған динамикалық шаманың орта мәндері бір-біріне тең және толық эквивалентті болады.Бірақ, уақыт бойынша орталау іш жүзінде мүмкін еместегін айттық. Сондықтан статистикалық әдіс бойынша орталау әлде қайда тиімді.
Таралу функциясын анықтау үшін, үлкен жүйе ішіндегі бір ғана кіші жүйені бақылаудың орнына бірдей көп кіші жүйелер жиынтығын қарастыру ыңғайлы. Бірдей бөліктерден тұраиын жүйелер жиынтығын – статистикалық ансамбль деп атайды. Ансамблдегі барлық кііш жүйелер саны N болсын.Кездейсоқ өлшеу кезінде олардың dn – і фазалық кеңістіктің dГ көлемі ішінде болсын дейік.Олай болса, таңдап алынған кіші жүйенің dГ көлем ішінде болу ықтималдығы былай анықталады:
dω=![]() (1.7)
(1.7)
Бұл ықтималдықтың шамасы және dn бөлшек саны,берілген dГ көлемінде пропорционал.Ал пропорционалдық коэффициенті,(1.2) бойынша,ықтималдықтың таралу функциясын береді.
Егер үлкен жүйе мен кіші жүйелер тепе-теңдікте тұрған болса,және кіші жүйелер өз кезегінде көп бөлшектен тұратын,статистикалық жүйе болса, онда кіші жүйені сипаттайтын кез келген динамикалық шаманың орта мәні уақытқа байланысты емес, тұрақты болады.Олай болса,динамикалық шаманың мәнін ұзақ уақыт бақылағанымызбен оның шын мәні,орта мәннен онша көп ауытқи қоймайды.Дәлірек айтсақ,орта мән төңірегіндегі ауытқу өте аз және сирек болады.Кіші жүйедегі бөлшек саны көп болған сайын ондай ауытқу азая түседі.Іс жүзінде ондай динамикалық шамалардың мәндерін тұрақты деп алуға болады.Бұл динамикалық шаманың f(q,p ) шын мәнінің, берілген мәнге ие болу ықтималдығының таралу функциясы p(q,p) , орта мән төңірегіне сәйкес, өте аз аралықта ғана 0- ден өзгеше болады.
Егер ансамбльдегі әртүрлі кіші жүйелер,алғашқы кезде әртүрлі күйлерде болған болса,яғни оларға сәйкес динамикалық шамалардың мәндері әртүрлі болса, біраз уақыттан соң олардың бәрі үлкен жүйемен тепе- теңдікке келеді де, бәрінің динамикалық шамалары бірдей, орта мәнде болады.Олай болса, статистикалық жүйелер үшін бастапқы шарттың әсері болмайды.Бұл тұрғыдан алғанда статистикалық болжам ықтималдықт сипатта емес, өте дәл деуге болады.
Егер тұйық жүйенің барлық бөліктері өзара тепе-теңдікте болса, онда оның кез келген бөлігіндегі динамикалық шамалардың мәндері бірдей және тұрақты болады.Мұндай жүйені- термодинамикалық тепе-теңдік жүйе дейміз.Тепе-теңдігі тұйық жүйенің өз бетімен тепе-теңдіктен ауытқуы өте сирек, іс жүзінде мүмкін емес деуге болады.Қандай да бір тұйық жүйе алғашқы кезде тепе-теңдікте болмаса, мысалы оның әр түрлі бөліктеріндегі динамикалық шамалардың орта мәндері әр түрлі болса, олардың бөлшектерінің өзара әсерлесу нәтижесінде, біраз уақыттан кейін жүйенің барлық бөлігінде тепе-теңдік орнайды.Тұйық жүйедегі тепе-теңдік орнау уақыты релаксация уақыты деп аталады.Әр түрлі жүйелер үшін релаксация уақыты да әр түрлі болады.Ол жүйенің физикалық қасиеттеріне байланысты,секундтың мыңнан бір бөлігінен бастап,бірнеше сағат, немесе тәулікке созылуы мүмкін.Біз берілген жүйені қзақ бақылаймыз деген кезде бақылау уақытын релаксация уақытымен салыстырғанда әлдеқайда үлкендігін айтамыз.
Біз статистикалық физикада тек тепе-теңдікте тұрған жүйелерді ғана қарастырамыз.
(1.5) формуласы бойынша есептелген орта мәндер үшін мынадай тұжырымдардың дұрыс болатындығын тексеріп көру қиын емес:
1. Тұрақты шаманың орта мәні өзіне тең ![]()
![]() с;
с;
2. Тұрақты көбейткішті интеграл алдына шығаруға болады ![]() =c
=c![]() ;
;
3. Қосындысының орта мәні,олардың орта мәндерінің қосындысына тең.![]() =
=![]() .
.
Қарастырып отырған динамикалық шаманың орта мәні, оның шын мәніне қаншалықты жақын екенін бағалау үшін,жүйенің тепе- теңдіктен ауытқуын зерттеу керек.Жүйенің тепе-теңдіктен өз беінше ауытқуын флуктуация дейді.Жүйе неғұрлым болған сайын ондағы флуктуацияның шамасы өте аз болады.Ауытқуды ![]() деп белгілеп алып,орташа ауытқуды есептесек, оның нөлге тең болатынын көреміз.
деп белгілеп алып,орташа ауытқуды есептесек, оның нөлге тең болатынын көреміз.![]() =
=![]() =
=![]() -
-![]() =0.Себебі,динамикалық шаманың шын мәнінің,оның орта мәннен жоғары және төмен ауытқулардың ықтималдықтары бірдей болады.Олай болса орташа ауытқу қойылған сұрауға жауап бере алмайды.Сондықтан орташа квадраттық ауытқу деген шама енгізу керек.Ол үшін алдымен ауытқудың квадратының орта мәнін есептейік.
=0.Себебі,динамикалық шаманың шын мәнінің,оның орта мәннен жоғары және төмен ауытқулардың ықтималдықтары бірдей болады.Олай болса орташа ауытқу қойылған сұрауға жауап бере алмайды.Сондықтан орташа квадраттық ауытқу деген шама енгізу керек.Ол үшін алдымен ауытқудың квадратының орта мәнін есептейік.
(![]() (
(![]() =
=![]() -2f
-2f![]() +(f
+(f![]() =
=![]() -2
-2![]() +
+![]() =
=![]() (
(![]() ) (1.8)
) (1.8)
Ауытқудың квадраты әр кез оң болатындықтың бұл шама нөлден өзгеше болады.Сондықтан,қарастырып отырған шаманың,орта мәннен қаншалықты ауытқығанын сипаттай алады.Ал ![]() -орташа квадраттық ауытқу деп аталады.Бұл шама өте аз болған жағдайда,динамикалық шаманың орта мәнін оның шын мәні деп алуға болады.Ауытқуды сипаттау үшін кейде салыстырмалы флуктуация енгізіледі.
-орташа квадраттық ауытқу деп аталады.Бұл шама өте аз болған жағдайда,динамикалық шаманың орта мәнін оның шын мәні деп алуға болады.Ауытқуды сипаттау үшін кейде салыстырмалы флуктуация енгізіледі.
![]() (1.9)
(1.9)
Егер ![]() болса,физиалық шаманың шын мәнінің, оның орта мәніне өте жақын болатынын көрсетеді.
болса,физиалық шаманың шын мәнінің, оның орта мәніне өте жақын болатынын көрсетеді.
Жүйе N бөліктен тұрадыдейік.Ондай жүйедегі кез келген аддитивті шаманың салыстырмалы флуктуациясы, бөлшек санының квадраттық түбіріне кері пропорционал болады.
![]() (1.10)
(1.10)
Егер жүйені сипаттайтын шама,олардың жеке бөліктеріндегі шамаларының қосындысына тең болса,ондай шама – аддитивті деп аталады.f![]() .Ықтималдықтарды қосу заңы бойынша,
.Ықтималдықтарды қосу заңы бойынша,
![]() =
=![]() . (1.11)
. (1.11)
Квадраттық ауытқудың орта мәнін есептейік.
![]() =
=![]() (1.12)
(1.12)
Оңай болу үшін бұл формуланы екі бөліктен тұратын жүйеге қолданайық.
![]()
Егер жүйенің бөліктері бір біріне тәуелсіз болса,онда тәуелсіз айнымалылардың көбейтіндісінің орта мәні,олардың орта мәндерінің көбейтіндісіне тең болады:
![]() =
=![]()
Орташа ауытқулар ![]() нөлге тең болғандықтан,
нөлге тең болғандықтан,
![]()
![]() ,
,
Яғни жүйенің квадраттық ауытқуы,оның жеке бөліктерінің квадраттық ауытқуларының қосындысына тең болады.Бұл айтылғанды N бөліктен тұратын жүйе үшін былай жазуға болады.
![]() =
=![]() (1.13)
(1.13)
Бұл формуланың оң жағындағы қосындылардың саны жүйедегі бөлшек санына тең.Егер бөліктер бірдей болса,ол қосылғыштардың шамалары да бірдей болады.Сондықтан (1.13) теңдеуінің оң жағы бөліктер санына пропорционал.Олай болса,
![]() (1.14)
(1.14)
Екінші жағынан,бірдей бөліктерден тұратын жүйе үшін,аддитивті шаманың орта мәні де бөліктер санына пропорционал болатындығын байқау қиын емес.![]() N.Олай болса,
N.Олай болса,
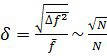 =
=![]() (1.15)
(1.15)
Макро денелердегі бөлшектер саны өте көп болатындықтан, салыстырмалы флуктуация нөлге жуық болады. Олай болса,үлкен жүйедегі ауытқу,ескеруге тұрмайтындай,өте аз. Жоғарыда келтірілген статистикалық орталаулар,іс жүзінде динамикалық шамалардың дәл мәнін көрсетеді.Статистикалық әдіс ықтималдыққа негізделгенмен,оның нәтижелері өте үлкен дәлдікпен берілген деуге негіз бар.
Ыдыс ішіндегі бір моль газдың қысымын өлшеу керек болсын. Қысым дегеніміз – молекулалардың ыдыс қабырғасына соқтығысу нәтижесінде,оның бір бірлік ауданына түсіретін күші.Соқтығысу кездейсоқ болғандықтан, қысымның шын мәні,оның орта мәніне барлық уақытта тең бола бермейді және уақыт бойынша өте тез өзгеріп отырады. Шын қысым, орта мәнінің төңірегінде аз флуктуация жасап тұрады.Бір моль газдағы молекулалар саны шамамен 6![]() болғандықтан, салыстырмалы флуктуация
болғандықтан, салыстырмалы флуктуация ![]() ,өте аз болады.Мұндай аз ауытқуды,өте дәл деген прибордың өзі сезе алмайды.Олай болса,тепе-теңдікте тұрған газ ішіндегі қысымды тұрақты деуге болады.
,өте аз болады.Мұндай аз ауытқуды,өте дәл деген прибордың өзі сезе алмайды.Олай болса,тепе-теңдікте тұрған газ ішіндегі қысымды тұрақты деуге болады.
1.4. Лиувилль теоремасы
N бөлшектен тұратын макро жүйе қарастырайық.Бұл жүйе басқа жүйенің кіші бөлігі болсын.Бөлшектердің қозғалыс заңдылығы классикалық Гамильтон теңдеулері арқылы берілсін:
![]() =
=![]() ,
,![]() =-
=-![]() , i=1,2,…,s (1.16)
, i=1,2,…,s (1.16)
Бұл жердегі H(q,p) – жүйенің Гамильтон функциясы.Әр бөлшектің еркінді дәрежесі үшке тең десек, жүйенің толық еркіндік дәрежесі s=3N болады. (1.16) теңдеулер жүйесін интегралдау арқылы, ![]() (t),
(t),![]() (t) функцияларын,яғни жүйенің күйін анықтай аламыз.Бұл 2s айнымалы, фазалық кеңістіктегі бір нүктені көрсетеді.Уақыт өткен сайын фазалық кеңістіктегі бейнелеуші нүкте белгілі бір траектория бойымен жылжып отырады. Фазалық траектория өзімен өзі қиылыспайды.Егер фазалық траектория бір нүктеде қиылысады десек, сол уақыт сәтіндегі бастапқы шарт белгілі болған жағдайда,жүйенің соңғы күйлері әр түрлі болар еді.Бұл себептілік принципіне қайшы келеді.
(t) функцияларын,яғни жүйенің күйін анықтай аламыз.Бұл 2s айнымалы, фазалық кеңістіктегі бір нүктені көрсетеді.Уақыт өткен сайын фазалық кеңістіктегі бейнелеуші нүкте белгілі бір траектория бойымен жылжып отырады. Фазалық траектория өзімен өзі қиылыспайды.Егер фазалық траектория бір нүктеде қиылысады десек, сол уақыт сәтіндегі бастапқы шарт белгілі болған жағдайда,жүйенің соңғы күйлері әр түрлі болар еді.Бұл себептілік принципіне қайшы келеді.
Кіші жүйенің күйін ұзақ уақыт бақылайық. Сол уақыт аралығын бірдей кіші интервалдарға бөліп,әрбір уақыт сәтіндегі жүйенің фазалық кеңістіктегі күйін белгілеп отырайық. Фазалық траектория өзімен өзі қиылыспайтындықтан,бір нүкте екі рет қайталанбайды.Ал жүйенің күйі үздіксіз өзгеріп отыратындықтан,қзақ уақыттан соң фазлық кеңістіктің dГ көлемі нүктелермен толық толады.Нүктелердің таралу тығыздығы бойынша, кіші жүйенің берілген күйде болуының ықтималдығының тығыздығын анықтай аламыз.
Бұл жерде кіші жүйені үлкен жүйеден тәуелсіз деп есептедік. Егер кіші жүйені ұзақ уақыт бақыласақ,оның үлкен жүйеге тәуелді екенін ескеру керек болар еді.Сондықтан,бақылау уақыты, кіші жүйе тәуелсіз деп айтарлықтай,аз болуы керек.
Бір кішкене жүйені бақылаудың орнына, бірдей N бөліктен тұратын жүйелер жиынын, яғни статистикалық ансамбль алуға болады.Бір уақыт сәтінде олардың күйлері, фазалық кеңістікте белгілі бір тығыздықпен таралған, N бейнелеу нүктесін береді.Бұл бейнелеу нүктелері уақытқа байланысты өз траекторияларын сызады.Тұтас жүйе тепе-теңдікте болғандықтан, фазалық кеңістіктегі бейнелеуші нүктелердің тығыздығы уақытқа байланысты емес, тұрақты болып қалады. Олай болса, әрбір нүкте төңірегіндегі ықтималдық тығыздығы p(q,p) функциясы бір мәнді анықталады.
Фазалық кеңістіктегі бейнелеуші нүктелер жиынын, формальді түрде, бөлшектер саны тұрақты, идеал газ деп есептеуге болады.Ондай газ 2s өлшемді кеңістікте ағады деп айтуға болады.Сондықтан бейнелеуші нүктелер үшін сақталу заңы болып табылатын, үздіксіздік теңдеуін жазуға болады.
![]() +div(pv)=0
+div(pv)=0
Бұл жердегі pv – ықтималдықтар ағынының тығыздығы, ал дивергенция 2s өлшемді кеңістікте алынған дербес туындылар қосындысы деп түсіну керек.Жоғарыда көрсетілгендей, ықтималдықтар тығыздығы уақытқа байланысты болмайтындықтан, үздіксіздік теңдеуін стационар күйін жазамыз.Стационар ағын үшін
div(pv)=0;
Дивергенцияның анықтамасы бойынша, соңғы теңдеуді былай ашып жазуға болады:
![]() (p
(p![]() )=0
)=0
Бұл жердегі ![]() – жалпылауыш координаталар мен импульстер жиынтығының жалпы белгісі, ал
– жалпылауыш координаталар мен импульстер жиынтығының жалпы белгісі, ал ![]() =
=![]() - жалпылауыш
- жалпылауыш ![]() жылдамдықтар
жылдамдықтар![]() ,олар координаталар мен импульстерден уақыт бойынша алынған туындылар.Соларды ескеріп, жоғарыдағы теңдеуді мына түрде жазуға болады:
,олар координаталар мен импульстерден уақыт бойынша алынған туындылар.Соларды ескеріп, жоғарыдағы теңдеуді мына түрде жазуға болады:
![]() =0.
=0.
Дербес туындыларды ашып жазайық:
![]() +
+![]() ]+p
]+p![]() +
+![]() ]=0 (1.17)
]=0 (1.17)
Соңғы қосынды астындағы туындыларды (1.16), Гамильтон теңдеулерін пайдаланып есептесек,
![]() =
=![]() = -
= - ![]()
Болатынын көреміз.Сондықтан (1.17) теңдеуіндегі екінші қосылғыш теңбе-тең нөлге айналады,ал бірінші қосылғыш,таралу функциясынан уақыт бойынша алынған толық туынды.
![]() =
=![]() +
+![]() ]=0 (1.18)
]=0 (1.18)
Бұл теңдеу,Лиувилль теоремасын білдіреді.Кіші жүйенің фазалық кеңістіктегі траекториясы бойындағы нүктелерде болу таралу функциясы тұрақты болып қалады.Бұл теорема квази тәуелсіз кіші жүйе үшін жазылғандықтан, оны бақылау уақыты онша үлкен емес деп есептейміз.
(1.18) теңдеуді, (1.16) Гамильтон теңдеулерін пайдаланып, мына түрде жазуға болады:
![]() =
=![]() -
-![]() ]=0 (1.19)
]=0 (1.19)
Классикалық механикада бұл қосындыны Пуассон жақшасы деп атайды және былай белгіленеді:
![]() -
-![]() ]=[p,H] (1.20)
]=[p,H] (1.20)
(1.19) теңдеуін, таралу функциясын табуға арналған,дербес туындылы дифференциалдық теңдеу деп қарастыруға болады. Бірақ бұл теңдеуді шешу, (1.6) қозғалыс теңдеулерін шешуден ооңай емес.Дегенмен бұл теңдеуді
![]() =0 (1.21)
=0 (1.21)
Түрінде жазу,таралу функциясының сипаты туралы маңызды мәлімет береді.Соңғы теңдеу – ықтималдық тығыздығының сақталу заңы, немесе Лиувилль теоремасы деп аталады.
Лиувилль теоремасын дәлелдеу кезінде таңдап алған жүйе тепе – теңдікте тұр деп есептедік. Көпшілік жағдайда тепе –теңдікте тұрмаған жүйені қарастыруға тура келеді.Жүйеде қандай да бір процесс жүріп жатса,мысалы алғашқыда тепе –теңдіктен шығарылған жүйені өзіне өзін берсек, онда оның тепе –теңдік қалыпқа ұмтылу процесі кезінде таралу функциясы уақытқа байланысты өзгереді.Мұндай процестер физикалық кинетика бөлімінде зерттеледі. Бұл кезде ықтималдық тығыздығы уақытқа айқын тәуелді болады. Ондай функцияның уақыт бойынша толық туындысы (1.19) ды ескеріп, былай есептеледі:
![]()
![]() =
=![]() -
-![]() ] (1.22)
] (1.22)
Жалпы жағдайда Лиувилль теоремасы мына түрде жазылады:
![]() [p,H]=0. (1.23)
[p,H]=0. (1.23)
1.5. Статистикалық жүйенің энергиясы.
Гиббстің микроканондық таралуы
Бірақ таралу функциясы жоғарыдағы қозғалыс интегралдарының бәріне бірдей тәуелді болмайтынын көрсетуге болады. Ол үшін үлкен жүйе ішінде, онымен тепе – теңдікте тұрған, екі кішкене жүйелерді қарастырайық.Олардың әрқайсысының таралу функцияларын ![]() және
және ![]() деп белгілейік.Олар негізі жүйемен тепе – теңдікте болғандықтан, екі кішкене жүйені біріктіріп, бір жүйе деп қарастырсақ та, олардың тепе – теңдігі бұзылмайды және оларды тәуелсіз жүйелер деп есептеуге болады.Біріккен жүйенің таралу функциясын
деп белгілейік.Олар негізі жүйемен тепе – теңдікте болғандықтан, екі кішкене жүйені біріктіріп, бір жүйе деп қарастырсақ та, олардың тепе – теңдігі бұзылмайды және оларды тәуелсіз жүйелер деп есептеуге болады.Біріккен жүйенің таралу функциясын ![]() десек,тәуелсіз оқиғалардың ықтималдықтарын көбейту заңы бойынша,
десек,тәуелсіз оқиғалардың ықтималдықтарын көбейту заңы бойынша, ![]() =
=![]()
![]() болады.Бұдан:
болады.Бұдан: ![]() =ln
=ln ![]() + ln
+ ln ![]() (1.24)
(1.24)
таралу функциясының логарифмі аддитивті шама болатынын көреміз. Олай болса, таралу функциясының логарифмі жай ғана қозғалыс интегралы емес – аддитивті қозғалыс интегралы деген тұжырым жасауға болады.
Тұйық механикалық жүйедегі сақталатын шамалар: энергия, толық импульстің үш құраушысы және импульс моментінің үш құраушысы, барлығы жеті қозғалыс интегралы, маңызды шамалар болып саналады.Бұл шамалардың әрқайсысы жалпылауыш координаталармен импульске тәуелді. Жүйенің ішіндегі әрбір кіші үшін ![]() (q,p)
(q,p) ![]() (q,p) ,
(q,p) , ![]() (q,p) . Бұл қозғалыс интегралдарынан, аддитивті скаляр шаманы бір ғана жолмен алуға болады. Ол үшін векторлық шамаларды белгісіз векторларға скаляр көбейтіп барып олардың қосындысын аламыз. Сонда, і- кіші жүйе үшін:
(q,p) . Бұл қозғалыс интегралдарынан, аддитивті скаляр шаманы бір ғана жолмен алуға болады. Ол үшін векторлық шамаларды белгісіз векторларға скаляр көбейтіп барып олардың қосындысын аламыз. Сонда, і- кіші жүйе үшін:
ln![]() =
=![]() (1.25)
(1.25)
Егер барлық кіші жүйелер бірдей болса, онда кіші жүйелер үшін а,b,c,d коэффициенттері де бірдей болады.
(1.25) теңдеуіндегі тұрақты а жай ғана нормалаушы коэффициент. Оны ![]() болатындай етіп таңдап алуға болады.Ал қалғандарын тұйық жүйедегі сақталатын шамалардың мәндеріне байланысты анықтау керек.Сонымен, сақталатын аддитивті жеті қозғалыс интегралы, тұйық жүйедегі статистикалық таралу функциясын толығымен анықтайды деген қорытынды жасаймыз.Бұл тұжырымның статистикалық физика үшін маңызы зор. Себебі, өте көп айнымалылар мен бастапқы щарттарға тәуелді қозғалыс теңдеулерін тікелей шешудің орнына, небәрі жеті тұрақтыға байланысты функцияны анықтасақ жеткілікті.Іздеп отырған таралу функциясы, сонымен бірге Лиувилль теоремасын қанағаттандыру керек.Ондай функцияны
болатындай етіп таңдап алуға болады.Ал қалғандарын тұйық жүйедегі сақталатын шамалардың мәндеріне байланысты анықтау керек.Сонымен, сақталатын аддитивті жеті қозғалыс интегралы, тұйық жүйедегі статистикалық таралу функциясын толығымен анықтайды деген қорытынды жасаймыз.Бұл тұжырымның статистикалық физика үшін маңызы зор. Себебі, өте көп айнымалылар мен бастапқы щарттарға тәуелді қозғалыс теңдеулерін тікелей шешудің орнына, небәрі жеті тұрақтыға байланысты функцияны анықтасақ жеткілікті.Іздеп отырған таралу функциясы, сонымен бірге Лиувилль теоремасын қанағаттандыру керек.Ондай функцияны ![]() (q,p)
(q,p) ![]() (q,p) ,
(q,p) , ![]() (q,p) аддитивті шамаларының фазалық кеңістікте тұрақты болып қалатын нүктелерінде, яғни тұйық жүйенің фазалық траекториясы бойында тұратын болатын p=const, ал қалған нүктелерде p=0 болатын функцияны алуға болады. Таралу функциясының фазалық траектория бойында тұрақты болуы, Лиувилль шартын қанағаттандыру үшін керек.Сақталу заңдарын мына түрде жазсақ,
(q,p) аддитивті шамаларының фазалық кеңістікте тұрақты болып қалатын нүктелерінде, яғни тұйық жүйенің фазалық траекториясы бойында тұратын болатын p=const, ал қалған нүктелерде p=0 болатын функцияны алуға болады. Таралу функциясының фазалық траектория бойында тұрақты болуы, Лиувилль шартын қанағаттандыру үшін керек.Сақталу заңдарын мына түрде жазсақ,
E(q,p)=![]() , P(q,p)=
, P(q,p)=![]() 6 L(q,p)=
6 L(q,p)=![]() , (1.26)
, (1.26)
бұл шамалардың тұрақты болатын нүктелерінің жиынтығы,2s-7 өлшемді кеңістіктегі жіңішке сызық болар еді.Олай болса, таралу функциясы ![]() шартын қанағаттандыру үшін, фазалық траектория бойында шексіздікке айналуы керек. Сондықтан ықтималдықтың таралу функциясын мына түрде жазған дұрыс:
шартын қанағаттандыру үшін, фазалық траектория бойында шексіздікке айналуы керек. Сондықтан ықтималдықтың таралу функциясын мына түрде жазған дұрыс:
p=const![]() (E-
(E-![]() )
)![]() (P-
(P-![]() )
)![]() (L-
(L-![]() ) (1.27)
) (1.27)
Бұл жердегі ![]() дельта- функциясы (
дельта- функциясы (![]() -функция) деп аталады.
-функция) деп аталады.![]() -функция мынадай шарт бойынша анықталған:
-функция мынадай шарт бойынша анықталған:
![]() (x-
(x-![]() )=
)=![]() (1.28)
(1.28)
Қозғалыс интегралдарының ең болмағанда біреуі,тиісті ![]() мәндеріне тең болмаған жағдайда,(1.27) түрдегі таралу функциясы нөлге айналады. (1.27) түрдегі функцияны – микроканондық таралу функциясы деп атайды.
мәндеріне тең болмаған жағдайда,(1.27) түрдегі таралу функциясы нөлге айналады. (1.27) түрдегі функцияны – микроканондық таралу функциясы деп атайды.
Тұйық жүйенің толық импульсі мен импульс моменті,оның біртұтас ілгерілемелі және айнымалы қозғалысын көрсетеді.Сондықтан тұйық жүйенің статистикалық қасиеттері импульс пен импульс моменттеріне байланысты болмайды.Олай болса, таралу функциясы тек энергияға ғана байланысты болады.Бұл, статистикалық жүйенің күйін анықтау үшін оның энергиясының ерекше орын алатынын көрсетеді.Энергия – жүйенің статистикалық қасиеттерін толық анықтайды.Сонда (1.25) теңдеуі мына түрде жазылады:
Lnp=a+bE(q,p) (1.29)
Бұдан микроканондық таалу функциясы былай жазылады:
P=const![]() (E-
(E-![]() ) (1.30)
) (1.30)
Бұл формула, тұйық жүйе үшін Гиббстің микроканондық таралуы деп аталады.
Кванттық бөлшектердің координата мен импульстерін бір мезгілде дәл көрсетуге болмайтындықтан, олардың фазалық кеңістіктегі күйін нүкте түрінде көрсету дұрыс емес.Сондықтан жүйенің фазалық траекториясы жіңішке сызық болмайды.Бұл жағдайда жүйенің күйі, фазалық кеңістіктегі, энергиясы (Е, Е+![]() ) аралығына келетін, жұқа қабатта жатады деген дұрыс.Сонда, тұйық жүйе үшін Гиббстің микроканондық таралуын мына түрде жазуға болады:
) аралығына келетін, жұқа қабатта жатады деген дұрыс.Сонда, тұйық жүйе үшін Гиббстің микроканондық таралуын мына түрде жазуға болады:
P(q,p)=![]() (1.31)
(1.31)
Бұл жердегі ![]() - жүйенің Гамильтон функциясы.
- жүйенің Гамильтон функциясы.
(1.31) формуласын, ![]() шекті жағдайда
шекті жағдайда ![]() - функция түрінде жазуға болады.
- функция түрінде жазуға болады.
p(H)=![]() (H-E) (1.32)
(H-E) (1.32)
![]() - функцияны Фурье интегралына жіктеп жазсақ:
- функцияны Фурье интегралына жіктеп жазсақ:
p(H)=![]() (1.33)
(1.33)
Бұл жердегі Ω – жұқа ![]() энергетикалық қабатқа сәйкес фазалық кеңістік бөлігінің көлемі.Белгілі таралу функциясы бойынша, кез келген динамикалық шаманың орта мәнін есептеуге болады. Таралу функциясын (1.33) түрінде алып, f(q,p) физикалық шамасының орта мәнін есептейік:
энергетикалық қабатқа сәйкес фазалық кеңістік бөлігінің көлемі.Белгілі таралу функциясы бойынша, кез келген динамикалық шаманың орта мәнін есептеуге болады. Таралу функциясын (1.33) түрінде алып, f(q,p) физикалық шамасының орта мәнін есептейік:
![]() (1.34)
(1.34)
Физикалық шаманың (1.6)арқылы есептелген,уақыт бойынша орта мәні, (1.5) немесе (1.34) фазалық кеңістік бойынша орта мәніне қаншалықты жақын екенін бағалау керек болсын.Егер фазалық траектория,![]() жұқа энергетикалық бетті қалдырмай,түгел толтыратын болса,уақыт бойынша және ансамбль бойынша орта мәндер өзара тең болады. Фазалық траекторияның айтылған энергетикалық бетті толық толтыруы – эргодикалық проблема деп аталады. Бұл терминді алғаш Больцман қолданған. Эргос -
жұқа энергетикалық бетті қалдырмай,түгел толтыратын болса,уақыт бойынша және ансамбль бойынша орта мәндер өзара тең болады. Фазалық траекторияның айтылған энергетикалық бетті толық толтыруы – эргодикалық проблема деп аталады. Бұл терминді алғаш Больцман қолданған. Эргос - ![]() энергия
энергия![]() , годос -
, годос - ![]() жол
жол![]() ,яғни энергетикалық бет бойындағы жол дегенді білдіреді.Бірақ фазалық траекторияның айтылған бетті түгел толтыруын қатаң дәлелдеу мүмкін болмады. Соңынан эргодикалық гпотезаның дұрыс емес екені белгілі болды,яғни жеке фазалық траектория бүкіл энергетикалық бетті толық толтыра алмайтыны дәлелденді.Сондықтан Больцман квазиэргодикалық гипотезаұсынды.Ол гипотеза бойынша, жеке фазалық траектория энергетикалық бетті түгел толтырмаса да, оның бетінен алынған кез келген нүктеге шексіз жақындайды деп есептеледі.
,яғни энергетикалық бет бойындағы жол дегенді білдіреді.Бірақ фазалық траекторияның айтылған бетті түгел толтыруын қатаң дәлелдеу мүмкін болмады. Соңынан эргодикалық гпотезаның дұрыс емес екені белгілі болды,яғни жеке фазалық траектория бүкіл энергетикалық бетті толық толтыра алмайтыны дәлелденді.Сондықтан Больцман квазиэргодикалық гипотезаұсынды.Ол гипотеза бойынша, жеке фазалық траектория энергетикалық бетті түгел толтырмаса да, оның бетінен алынған кез келген нүктеге шексіз жақындайды деп есептеледі.
Математикада көп өлшемді кеңістіктің топологиясын зерттейтін арнайы тақырып пайда болды. Онда эргодикалық проблема жан – жақты зерттелген.
1.6. Кванттық жүйелердің ерекшеліктері
Көп бөлшектен тұратын жүйенің статистикалық сипатын кванттық тұрғыдан зерттеу үшін оның құрамындағы бөлшектердің кванттық қасиеттері ескерілу керек.Көп бөлшектен тұратын жүйе ,үшін Шредингер теңдеуін шешу, қозғалыс теңдеулерін интегралдауға қарағанда, әлдеқайда күрделі. Тіпті Шредингер теңдеуін, қандай да бір жолмен шешкен күннің өзінде, оның белгілі бір шарттарды қанағаттандыратын толқындық функциясын жазу және одан пайдалы информация алу мүмкін емес.
Энергетикалық деңгейлердің өте жиі орналасуынан кванттық жүйе белгілі бір энергияға сәйкес, стационар күйде бола алмайды. Берілген жүйенің оны қоршаған ортамен әлсіз әсерлесуінің өзі жүйенің күйін өзгертіп жібереді. Жүйе қаншалықты оқшауланған дегенімізбен, дүниеде абсолют тұйық жүйе болмайды. Тіпьі тұйық жүйенің энергиясының дәл мәнін көрсету мүмкін емес. Ондай жүйенің энергиясын өлшеу үшін, оған сырттан өлшеуіш прибор арқылы әсер ету керек. Егер жүйе өлшеуге дейін Е деңгейде болған десек, өлшеуіш прибормен әсерлесу нәтижесінде өз күйін өзгертіп, ![]() деңгейге көшуі мүмкін. Бұл күйлердегі энергия анықталмағандығы,
деңгейге көшуі мүмкін. Бұл күйлердегі энергия анықталмағандығы, ![]() болатын өлшеу уақытының ұзақтығына байланысты.
болатын өлшеу уақытының ұзақтығына байланысты.
![]()
Екі күйдегі энергияны өлгеу қателіктері шамалас болғандықтан,
![]() деп алуға болады. Жүйені стационар күйде тұр деп есептеу үшін,
деп алуға болады. Жүйені стационар күйде тұр деп есептеу үшін, ![]() - тің шамасы, энергетикалық деңгейлер арасынан әлдеқайда кіші болу керек. Ал энергетикалық деңгейлер арасы елеуге тұрмайтындай аз болғандықтан, жүйені стационар күйге келтіру үшін шексіз ұзақ уақыт күтуге тура келер еді. Олай болса, макро жүйелердің қатаң стационар күйлері болмайды.Макро денелердің күйін толқындық функциялар толық анықтай алмайды.
- тің шамасы, энергетикалық деңгейлер арасынан әлдеқайда кіші болу керек. Ал энергетикалық деңгейлер арасы елеуге тұрмайтындай аз болғандықтан, жүйені стационар күйге келтіру үшін шексіз ұзақ уақыт күтуге тура келер еді. Олай болса, макро жүйелердің қатаң стационар күйлері болмайды.Макро денелердің күйін толқындық функциялар толық анықтай алмайды.
Олар физикалық шамалардың берілген мәндерге ие болуының ықтималдығын ғана көрсетеді.
Кванттық механикада әрбір физикалық шамаға сызықты, эрмиттік оператор сәйкес келетіндігі көрсетіледі.f![]() .Мысалы жүйенің толық энергиясына Гамильтон операторы сәйкес келеді E
.Мысалы жүйенің толық энергиясына Гамильтон операторы сәйкес келеді E![]() .
.
Макро жүйенің бөлігі болатын, кіші жүйе қарастырайық. Егер кіші жүйенің үлкен жүйемен әсерлесуін ескермесек, оның күйін жуықтап стационар деп есептеуге болады. Ал жүйенің стационар күйін белгілі Шредингер теңдеуін шешу арқылы анықтауға болады.
![]() (q)=
(q)=![]() (q) (1.35)
(q) (1.35)
Мұндағы ![]() n – стационар күйдің энергиясы, ал q – кіші жүйені сипаттайтын барлық координаталар жиыны.
n – стационар күйдің энергиясы, ал q – кіші жүйені сипаттайтын барлық координаталар жиыны.
Макро жүйе толық стационар күйде бол алмайтындықтан, таңдап алған кіші жүйенің толқындық функциясын, (1.35) Шредингер теңдеуінің шешімдері болатын, ![]() , толық ортогональ функциялар жүйесіне жіктеу түрінде алайық.
, толық ортогональ функциялар жүйесіне жіктеу түрінде алайық.
𝜓(q)=![]() (q) (1.36)
(q) (1.36)
Осы күйде тұрған жүйе үшін физикалық шаманың орта мәні былай анықталады:
![]() (q)
(q)![]() (q)dq (1.37)
(q)dq (1.37)
Бұл формулаға (1.36) жіктеуін қойып, матрицалық элементті былай белгілесек,
![]() (q)
(q)![]() (q)dq (1.38)
(q)dq (1.38)
Берілген шаманың орта мәнін мына түрде көрсетуге болады:
![]() =
=![]() (1.39)
(1.39)
Матрицалық элементтің модулінің квадраты ![]() , жүйенің m – күйден n – күйге көшуінің ықтималдығын береді.Бұд жердегі
, жүйенің m – күйден n – күйге көшуінің ықтималдығын береді.Бұд жердегі ![]() көбейтіндісін, екі индекске тәуелді матрица деп есептейік.Бұл матрица
көбейтіндісін, екі индекске тәуелді матрица деп есептейік.Бұл матрица ![]() күйлерді сипаттайды дейді,ал (1.39) формуласын, әр түрлі таза күйлер бойынша орталау деп түсіну керек.Ондай орталауды сандардың көбейтіндісі емес, бір матрица арқылы жүргізілген десек,
күйлерді сипаттайды дейді,ал (1.39) формуласын, әр түрлі таза күйлер бойынша орталау деп түсіну керек.Ондай орталауды сандардың көбейтіндісі емес, бір матрица арқылы жүргізілген десек,
![]() (1.40)
(1.40)
Сонда (1.39) формуласы былай жазылады.
![]() =
=![]() (1.41)
(1.41)
Бұл жердегі ![]() ,энергетикалық өрнектеуге берілген, ықтималдық тығыздығының матрицасы, немесе статистикалық матрица деп аталады.
,энергетикалық өрнектеуге берілген, ықтималдық тығыздығының матрицасы, немесе статистикалық матрица деп аталады.
Тығыздық матрицасы бойынша,бірдей кванттық механикалық жүйелер ансамбльінің күйлері сипатталады.Бұл жағдайда да,классикалық Гиббс ансамбліндегідей,сыртқы шарттар,жүйенің кванттық механикалық күйлерін анықтауға толық жетпейді.Біз тек жүйенің берілген күйде болу ықтималдығын ғана көрсете аламыз.Сондықтан,тығыздық матрицасын жүйені толық емес сипаттау үшін қолданамыз.
Егер ![]() матрицасының элементтерін
матрицасының элементтерін ![]() статистикалық операторы деп қарастырсақ,
статистикалық операторы деп қарастырсақ,![]() қосындысы n бойынша есептеп,оны,
қосындысы n бойынша есептеп,оны, ![]() операторлар көбейтіндісіне сәйкес матрицаның диагональ элементтері деуге болады,ал орта мән,осы операторға сәйкес матрицаның диагональ элементтерінің қосындысы,яғни
операторлар көбейтіндісіне сәйкес матрицаның диагональ элементтері деуге болады,ал орта мән,осы операторға сәйкес матрицаның диагональ элементтерінің қосындысы,яғни ![]() ізі
ізі![]() арқылы анықталады.
арқылы анықталады.
![]() =
=![]() =Sp
=Sp![]() )
)
Тығыздық матрицасын,кванттық механикалық жүйе туралы мағлұматтар толық болмаған жағдайда,жүйені сипаттау үшін қолданады.Тығыздық матрицасы белгілі болған жағдайда,кез келген шаманың орта мәндерін анықтауға болады және оның берілген мәндерді иелену ықтималдылықтары көрсетіледі.Бұл жердегі толық емес сипаттау деуіміз,шамалардың мүмкін болатын мәндерінің ықтималдығын көрсетуіне байланысты айтылып отыр.Ал кванттық жүйені толық сипаттау үшін,Шредингер теңдеуін шешіп,толқындық функцияларды анықтау керек,бірақ бұл макро жүйелер үшін мүмкін емес екенін жоғарыда айттық.![]() сипаттау,шартты түде алынып отыр.Шындығында,макро кванттық жүйелер үшін,тығыздық матрицасы арқылы анықталған шамалардың ортамәндерінің,олардың шын мәндерінен ауытұуы,классикалық жағдайдағыдай,өте аз болады.Бұл жағдай да,жүйедегі бөлшек сандары артқан сайын,аддитивті шамалардың салыстырмалы флуктуациясы нөлге жуық болады.
сипаттау,шартты түде алынып отыр.Шындығында,макро кванттық жүйелер үшін,тығыздық матрицасы арқылы анықталған шамалардың ортамәндерінің,олардың шын мәндерінен ауытұуы,классикалық жағдайдағыдай,өте аз болады.Бұл жағдай да,жүйедегі бөлшек сандары артқан сайын,аддитивті шамалардың салыстырмалы флуктуациясы нөлге жуық болады.
Қорытынды:
Қорыта келгенде, Кез келген макро дене өте көп атомдар мен молекулалардан және олар өзара өте күрделі заңдылықпен әсерлеседі.Бізді Қоршаан ортадаы макро денлердің және олардың бөліктерінің өзара әсерлесуінде тек электромагнитті күштерді ескеру жеткілікті.Себебі олардың арсындағы гравитациялық әсерлесу,шектен тыс аз болғандықтан ескеруге тұрмайды.Ал ядролық әсерлесулер ![]() см аралықта ғана, ядроның көлемінде білінетіндіктен және ядролар бөлінбейді деп есептесек,ядролық күштерді де ескермеуге болады.Сонымен, макро денелердің күйін электромагниттік күштер ғана анықтайды.Ал ол күштердің табиғаты классикалық электродинамикада жеткілікті зерттелген.
см аралықта ғана, ядроның көлемінде білінетіндіктен және ядролар бөлінбейді деп есептесек,ядролық күштерді де ескермеуге болады.Сонымен, макро денелердің күйін электромагниттік күштер ғана анықтайды.Ал ол күштердің табиғаты классикалық электродинамикада жеткілікті зерттелген.
Фазалық кеңістік ұғымын жете түсіну үшін, бір еркіндік дәрежесі бар жүйе қарастырайық.Яғни кеңістіктегі Х осінің бойымен қозғалатын,массасы m бір бөлшекті алайық.Ондай жүйенің фазалық кеңістігі екі өлшемді (q,p) жазықтығы болады.Егер әрбір уақыт сәтіндегі координата мен импульстің уақытқа байланысты функциясы q(t),p(t) белгілі болса,олар фазалық жазықтықтағы траекторияның параметрлік теңдеуі болып табылады.Егер олардағы уақытты шығарып тастасақ,p=p(q) теңдеуі фазалық траекторияның канондық теңдеуін береді.
Лиувилль теоремасы бойынша, тепе – теңдіктегі жүйе үшін ықтималдық тығыздығы функциясы сақталу үшін, (1.20) Пуассон жақшасы нөлге тең болуы керек.Басқаша айтқанда, тұйық жүйенің таралу функциясы, сақталатын шамаларға ғана тәуелді болу керек. Механикада сақталатын негізгі инварианттар – жүйенің импульсі, импульс моменті және энергиясы екендігі белгілі.Бұлар,барлығы жеті қозғалыс интегралдарын береді.Таралу функциясы жалпылауыш координаталар мен импульске тікелей байланысты емес, қозғалыс интегралдары арқылы тәуелді болады.Таралу функциясы қозғалыс интегралдарына ғана байланысты болса, оның өзі де инвариантты шама болады.
Көп бөлшектен тұратын жүйенің статистикалық сипатын кванттық тұрғыдан зерттеу үшін оның құрамындағы бөлшектердің кванттық қасиеттері ескерілу керек.Көп бөлшектен тұратын жүйе ,үшін Шредингер теңдеуін шешу, қозғалыс теңдеулерін интегралдауға қарағанда, әлдеқайда күрделі. Тіпті Шредингер теңдеуін, қандай да бір жолмен шешкен күннің өзінде, оның белгілі бір шарттарды қанағаттандыратын толқындық функциясын жазу және одан пайдалы информация алу мүмкін емес.
Пайдаланылған әдебиеттер:
1. Ноздрев.В.Ф, Сенкевич.А.А. Курс статистический физики. Москва. Высшая школа. 1969.
2. Сирота.Н.Н. Термодинамика и статистическая физика. Минск. Высшая школа. 1969.
3. Румер.Ю.Б, Рывкин.М.М. Термодинамика и статистическая физика и кинетика. Москва <<наука>> 1972
4. Задачи по термодинамике и статистической физике.Под.ред.П.Ландсберга.Москва,Мир,1974
5. Истеков.К.К, Косов.В.Н, Д.П.Стрыгин статистическая физика.Основы физической кинетики.Алматы.ТОО Триумф <<Т>> 2007.
6. Серова.Ф.Г, Янкина.А.А. Задачник – практикум по термодинамике.Москва.Просвещение,1972.
7. Ландау.Л.Д, Лифшиц.Е.М. статистическая физика. Курс теоритической физики. Москва, Посвещение,1985
8. Базаров.И.П. Термодинамика и статистическая физика. Москва, Изд-во МГУ,1989
9. Кондратьев.А.С, Ромков.В.С. Задачи по статистической физике.Москва,Высшая школа,1992
10. Василевский.А.С, Мултановский.В.В. Статистическая физика и термодинамика.Москва <<Провещение>> 1985.
11. Леонтович.М.А. Введение в термодинамику.Статистическая физика Москва <<наука>> 1983.
12. Васильев.А.М. Введение в статистическую физику Москва <<Высшая школа>> 1980.
Похожие материалы
... б) Физикалық, процестерді модельдегенде, кейбір құбылыстарды сөзбен тусіндіру, көзбен көру қиын бола- тын есептер. Тандалынып алынатын есептер ЭЕМ-нің көмегімен шығару тиімді екенін керсете алатындай болуы керек. Олардың ішінде техниқалық объектінің немесе нақты физикалық модельді есептеуге ...
... арнайы шұңқырларға салынып, залалсыздандыру жұмысын жүргізіп отырады. Берілген дипломдық жұмыс «Қарағанды қаласының сауда орталықтарына келіп түсетін ысталған балықты ветеринарлық-санитарлық сараптауға» байланысты біз ысталған балықтардың құрамында&# ...
... Магистерлік диссертацияның мақсаты. Байланыстың үзілісіздігін және қызмет көрсету сапасын арттыру мақсатында телекоммуникациялық желілердің өміршеңділігін бағалайтын әдістеме құру. Магистерлік диссертацияның ғылыми жаңалығы. Максималды ақпарат ағыны матрицасы мен е&# ...





0 комментариев