2.1 Теоретические сведения
Синтез включает в себя следующие этапы:
а) словесная формулировка задачи. На этом этапе словесно описывается, как должна работать синтезируемая схема;
б) составление таблиц истинности. На этом этапе определяется количество переменных, функциональных узлов и количество выходов. Затем для каждого выхода функционального узла и всей схемы составляется таблица истинности;
в) минимизация функций, представленных в виде таблиц истинности. Выражение функции, получаемое непосредственно из таблицы истинности, как правило, избыточно, и его необходимо упростить (минимизировать) одним из известных способов. Но нужно учитывать, что эти способы минимизации уменьшают только количество переменных и операций, но не учитывают другие факторы (число элементов в корпусе, максимальное быстродействие и т. д.);
г) перевод минимизированных функций в нужный базис. Для этого используется правило де Моргана;
д) составление принципиальной электрической схемы. При составлении схемы учитываются особенности логических элементов (ЛЭ) выбранной серии: уровни сигналов, напряжение питания, нагрузочную способность, быстродействие и т. д. Схема составляется так, чтобы было использовано минимальное количество корпусов интегральных схем. Неиспользуемый ЛЭ интегральной схемы с n входами можно использовать как ЛЭ с меньшим числом входов. На все неиспользуемые входы ЛЭ должны быть поданы уровни сигналов, соответствующие логике работы ЛЭ;
е) подключение к логической схеме конечной нагрузки. Если ток и (или) напряжение нагрузки не соответствуют выходным параметрам ЛЭ, к которому должна подключаться нагрузка, то между ними устанавливается согласующий элемент (ЛЭ с повышенной нагрузочной способностью, транзистор, реле и т. д.).
Минимизацию функций, содержащих не более 6 переменных, удобно осуществлять с помощью карт Карно. Карта Карно составляется по определенному правилу. Один из вариантов карты Карно для четырех переменных, которым и рекомендуется пользоваться, показан на рисунке 3.1.
Такую карту Карно можно использовать и для меньшего числа переменных, считая, что неиспользованные клетки просто отсутствуют. Области переменных X iобозначены чертой (например, к области переменных Х 3 относятся клетки 4,5,6,7,12,13,14,15). Области переменных ![]() лежат вне черты. Младшая переменная обозначается Х 1, а старшинство остальных переменных линейно возрастает с увеличением индекса. Таким образом, в карте Карно, показанной на рисунке 3.1, имеются области
лежат вне черты. Младшая переменная обозначается Х 1, а старшинство остальных переменных линейно возрастает с увеличением индекса. Таким образом, в карте Карно, показанной на рисунке 3.1, имеются области ![]()
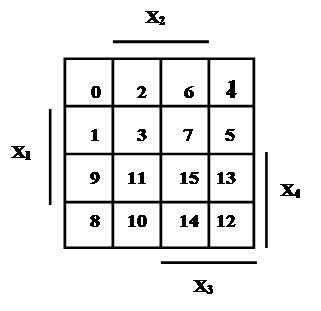
Рисунок 2.1
Карта Карно заполняется по таблице истинности или по аналитическому выражению функции, которую нужно минимизировать.
В карте Карно, показанной на рисунке 2.1, номера клеток соответствуют номерам строк таблицы истинности (числу, которое выражает двоичная комбинация значений переменных, находящихся в данной строке). Поэтому при заполнении данной карты Карно по таблице истинности значение функции из строки с каким-либо номером переносится в клетку карты Карно с таким же номером.
Для не полностью определённой функции в клетки, соответствующие неиспользуемым комбинациям, ставятся либо нули, либо единицы таким образом, чтобы минимизированное выражение функции получилось минимальным.
Если функция задана аналитически, её сначала приводят к дизъюнктивной нормальной форме, т.е. форме, где инверсии стоят только над отдельными переменными. Это можно сделать, используя правило преобразования функций и теорему де Моргана. В процессе заполнения карты Карно единицы устанавливаются в те клетки, которые находятся в зоне пересечения областей переменных, (одновременно принадлежат областям переменных) входящих в данную конъюнкцию. Расстановка единиц применяется для всех конъюнкций заданного выражения. Если в клетке уже установлена единица при заполнении по предыдущим конъюнкциям, то единица остаётся. Конъюнкция может включать от одной переменной данного набора переменных до полного набора всех переменных данного набора.
В клетках, где не установлены единицы, устанавливаются нули.
Например, необходимо для выражения ƒ(ν) = ![]() заполнить карту Карно. В это выражение входит сложная конъюнкция
заполнить карту Карно. В это выражение входит сложная конъюнкция ![]() . Применяя для неё правило де Моргана, получим
. Применяя для неё правило де Моргана, получим ![]() =
= ![]() . В дизъюнктивной нормальной форме заданная функция имеет вид ƒ(ν) =
. В дизъюнктивной нормальной форме заданная функция имеет вид ƒ(ν) = ![]() и состоит из трёх конъюнкции. Первая конъюнкция включает в себя одну переменную
и состоит из трёх конъюнкции. Первая конъюнкция включает в себя одну переменную![]() , значит, единицы устанавливаются в клетках 0,1,4,5,8,9,12,13, которые принадлежат области
, значит, единицы устанавливаются в клетках 0,1,4,5,8,9,12,13, которые принадлежат области ![]() .Вторая конъюнкция включает в себя тоже одну переменную
.Вторая конъюнкция включает в себя тоже одну переменную ![]() . Единицы устанавливаются в клетках 0,2,4,6,8,10,12,14 (в клетках 0,4,8,12, они уже установлены и сохраняются). Третья конъюнкция включает в себя три переменных
. Единицы устанавливаются в клетках 0,2,4,6,8,10,12,14 (в клетках 0,4,8,12, они уже установлены и сохраняются). Третья конъюнкция включает в себя три переменных ![]() ,
, ![]() ,
, ![]() . В зону перекрытия областей
. В зону перекрытия областей ![]() ,
, ![]() ,
, ![]() входят одновременно только две клетки 6 и 7. В клетке 6 единица уже стоит, и поэтому единица устанавливается только в клетке 7. В остальные клетки 3,11,15 устанавливаются нули. Карта Карно заполнена.
входят одновременно только две клетки 6 и 7. В клетке 6 единица уже стоит, и поэтому единица устанавливается только в клетке 7. В остальные клетки 3,11,15 устанавливаются нули. Карта Карно заполнена.
Минимизация осуществляется следующим образом. Все клетки, содержащие 1 (или 0) должны быть объедены в группы. В группы объединяются соседние клетки, содержащие 1 (или 0) и образующие прямоугольники с количеством клеток 2 n, где n = 0, 1, 2, 3 и т. д. Клетки с 1 (или 0 ), которые невозможно объединить с другими, образуют группы с числом клеток 1. Одна и та же клетка может входить в несколько групп. При определении соседних клеток карту Карно можно сворачивать в рулон по горизонтали и по вертикали. Равнозначных вариантов склеивания может быть несколько.
Чтобы выражение функции получилось минимальным, необходимо создавать минимальное число групп, при максимально возможном числе клеток в группе.
Минимизированную функцию записывают в следующем виде при склеивании клеток с единицами:
![]()
при склеивании клеток с нулями:
![]() ,
,
где Сi – выражение для i – ой группы; m – количество групп.
Выражение для группы – это конъюнкция тех переменных с инверсией или без инверсии (но не одновременно), в области которых группа находится вся целиком. Чем больше клеток содержится в группе, тем в меньшем числе областей переменных группа находится вся целиком.
При необходимости полученное выражение функции переводится в нужный базис помощью теоремы де Моргана.
Напряжение питания для микросхем серий ТТЛ – 5 В, для серий КМОП выбирается наиболее рациональное в пределах допустимого. Если напряжение питания микросхемы меньше напряжения питания нагрузки, то в выходном каскаде необходимо использовать логический элемент с открытым коллектором и включать нагрузку, как показано на рисунке 2.2 а). Если источник питания один и тот же для нагрузки и микросхемы, то выход логического элемента на рисунке 3.2а) может быть и нормальным. В любом случае допустимый выходной ток микросхемы должен быть не меньше, чем ток нагрузки. Обычно в выходном каскаде используются микросхемы с выходом, который имеет повышенную нагрузочную способность.
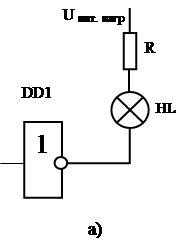
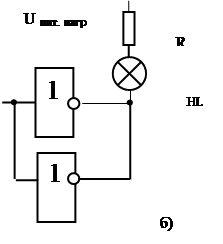
Рисунок 2.2
Если логический элемент с нужным током не найден, то можно два элемента включить параллельно, как показано на рисунке 2.2 б). Допустимая нагрузка в этом случи на каждый элемент составляет 0,9 от его максимальной. Выходной логический элемент может быть как с инверсным выходом так и с прямым (например, повторитель).
Резистор R ограничивает ток в нагрузке до номинального и определяется достаточно точно по формуле:
R = (U пит / I ном ) – R нагр = ( U пит – U ном ) / I ном
Если в сериях КМОП не найдется варианта для выходного каскада, обеспечивающего заданный ток нагрузки, то выходной каскад выполняется на элементах ТТЛ и согласуется при необходимости по току и напряжению с остальной частью схемы.
При напряжении питания нагрузки меньше 15 В, напряжение питания ЛЭ КМОП рациональнее выбирать равным напряжению питания нагрузки, а при напряжении питания нагрузки больше 15 В равным одному из стандартных значений (5, 12, 15 В) в пределах допустимого для выбранной серии.
В целях уменьшения числа корпусов интегральных схем неиспользуемый логический элемент микросхемы с большим числом входов может быть использован для реализации элемента с меньшим числом входов и наоборот.
Пример выполнения задания.
Номера клеток карты Карно, в которых стоят единицы: 0,1,2,3,7,10,11,13. Мощность лампы РHL = 220мВт, номинальное напряжение лампы 6,3 В, напряжение источника питания для нагрузки 12 В.
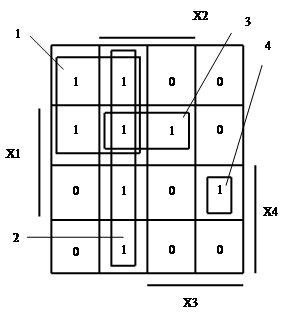
1) Заполненная карта Карно показана на рисунке 3.4
2) Таблица истинности, составленная по карте Карно, показана на рисунке 3.3
3) Выражения функции в СДНФ, полученное по таблице, истинности:
![]()
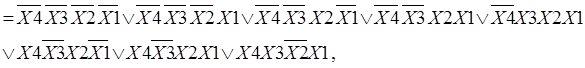
где Кi – i-ый минтерм.
4) Объединение в группы единичных клеток показано на рисунке 3.4 а), а нулевых клеток на рисунке 3.4 б).
Из рисунка 3.4 а) видно, что при объединении клеток, содержащих 1, получается четыре группы: две из четырех клеток, одна из двух клеток и одна из одной клетки. При объединении клеток содержащих 0, получается тоже четыре группы: одна из четырех клеток (карту Карно можно сворачивать по горизонтали и по вертикали), и три из двух клеток.
Выражение минимизированной функции при объединении единичных клеток
![]() (3.1)
(3.1)
при объединении нулевых клеток
5) Номинальный ток лампы
IHL=![]()
Напряжение питания схемы на ЛЭ КМОП рациональнее принять 12 В, а для схем на ЛЭ ТТЛ оно стандартное 5 В. Выходной элемент должен выдерживать ток 34.9 мА и для ЛЭ ТТЛ иметь открытый коллектор и допустимое напряжение больше 12 В.
|
I |
Х4 |
Х3 |
Х2 |
Х1 |
f(ν) |
|
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
2 |
0 |
0 |
1 |
0 |
1 |
|
3 |
0 |
0 |
1 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
0 |
|
5 |
0 |
1 |
0 |
1 |
0 |
|
6 |
0 |
1 |
1 |
0 |
0 |
|
7 |
0 |
1 |
1 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
0 |
|
9 |
1 |
0 |
0 |
1 |
0 |
|
10 |
1 |
0 |
1 |
0 |
1 |
|
11 |
1 |
0 |
1 |
1 |
1 |
|
12 |
1 |
1 |
0 |
0 |
0 |
|
13 |
1 |
1 |
0 |
1 |
1 |
|
14 |
1 |
1 |
1 |
0 |
0 |
|
15 |
1 |
1 |
1 |
1 |
0 |
Рисунок 2.3
 б)
б)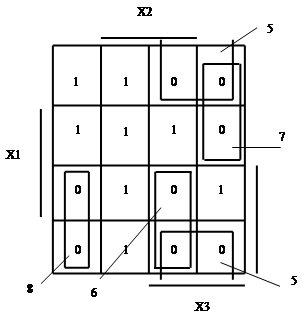
Рисунок 2.4
Из анализа выражения (3.1) следует, что в выходном каскаде должен находиться четырехвходовой элемент ИЛИ. Среди элементов серии ТТЛ четырёхвходового элемента ИЛИ с открытым коллектором нет. Поэтому для подключения лампы используются схема, показанная на рисунке 3.2 а). При единичном значении сигнала на входе инвертора, на его выходе ноль и лампа загорается. В данном случае можно использовать микросхему 155ЛН3. Её допустимый нулевой выходной ток IOL= 40мА.
Сопротивление ограничивающего резистора
![]()
Принимается стандартное значение 160 Ом.
Из анализа выражения (3.2) следует, что в выходном каскаде должен находиться четырехвходовой элемент ИЛИ-НЕ. Среди элементов серии КМОП нет четырёхвходового элемента ИЛИ-НЕ с допустимым током больше 34.9 мА. Подходящим элементом для подключения лампы может служить микросхема 564ЛА10, которая содержит два элемента 2И-НЕ с открытым стоком. При напряжении 15 В её допустимый выходной ток 100 мА. Элемент 2И-НЕ используется, как инвертор.
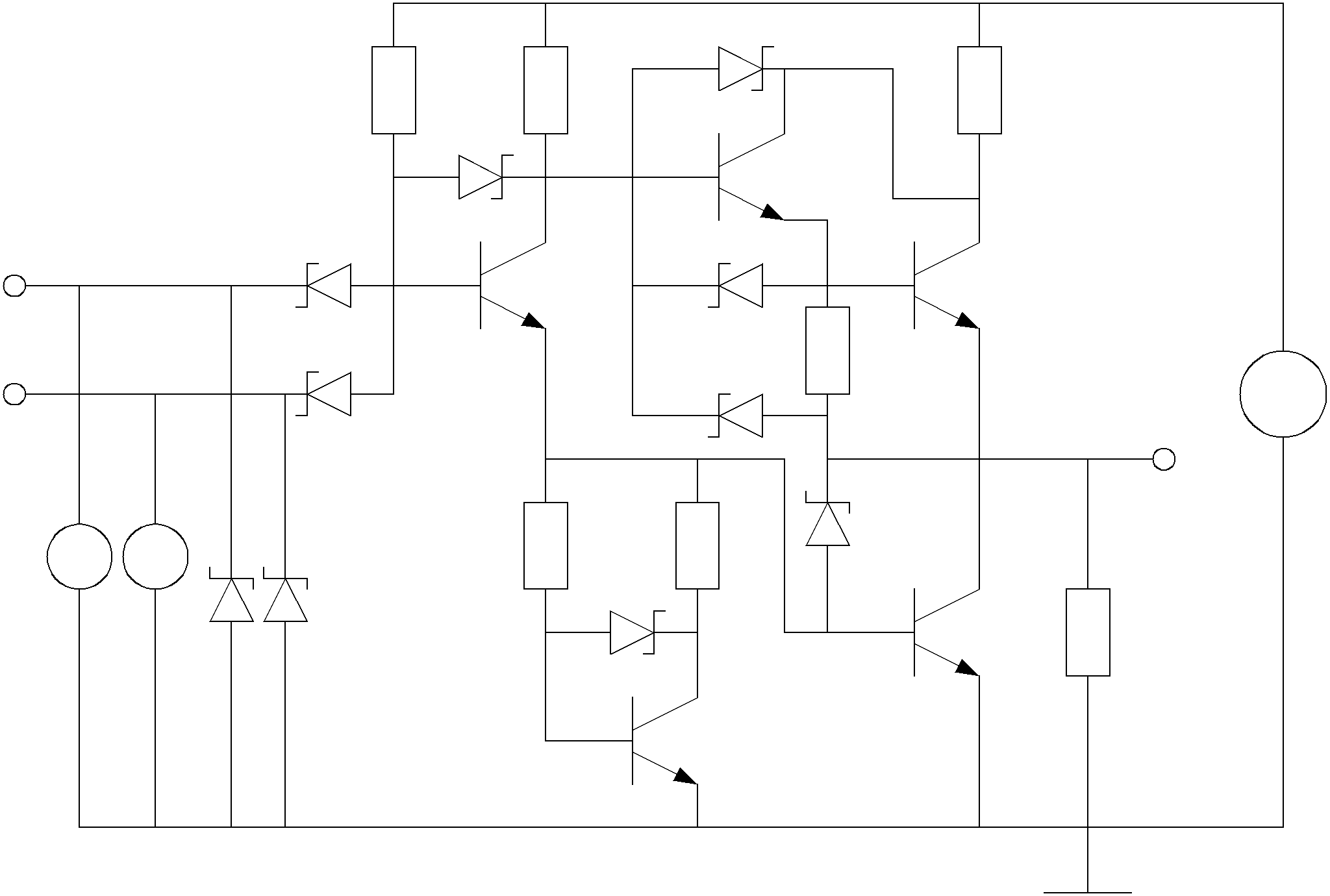
6) Для схемной реализации выражения (3.1) в базисе И,ИЛИ,НЕ необходимо три инвертора (чтобы получить инверсные значение переменных), один четырёх- входовой элемент ИЛИ, по одному трёх- и четырёхвходовому элементу И и два двухвходовых элементов И. Четырёхвходовой элемент ИЛИ отсутствует, поэтому для его реализации используются три двухвходовых элемента ИЛИ микросхемы 1533ЛЛ1. В качестве трёхвходового элемента И используются свободный четы-рёхвходовый элемент И микросхемы 1533ЛИ6. Инверсия переменных осуществляется свободными инверторами микросхемы 155ЛН3 с дополнительными резисторами в коллекторной цепи. Их значение можно принять 1 кОм. Таким образом, для схемной реализации функции в базисе И, ИЛИ, НЕ потребовалось четыре корпуса микросхем. Схема показана на рисунке 2.5
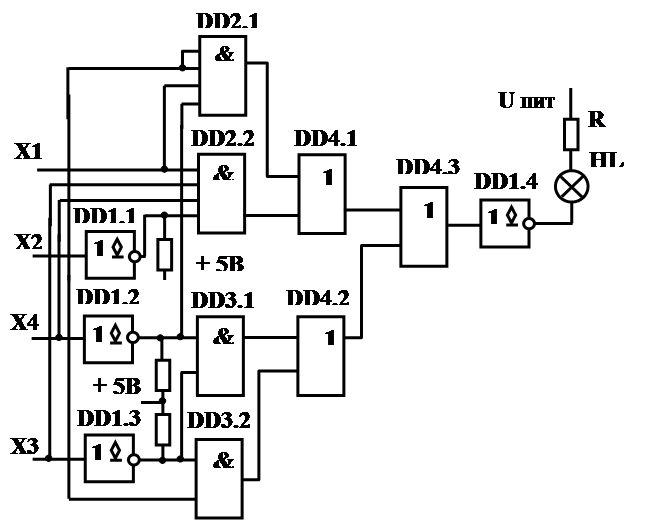
DD1 К1533ЛН2
DD2 К1533ЛИ6
DD3 К1533ЛИ1
DD4 К1533ЛЛ1
Рисунок 2.5
7. Для реализации выражения (3.2) в базисе ИЛИ-НЕ его необходимо преобразовать с помощью теоремы де Моргана к виду
![]()
В схеме нужно использовать один четырехвходовой, два трехвходовых и один двухвходовой элемент ИЛИ-НЕ. Требуется также четыре инвертора. Двух-входной элемент создаётся из свободных четырёхвходового или трёхвходового элемента ИЛИ-НЕ.
Таким образом, необходимо четыре корпуса микросхем: 564ЛЕ10 (4ИЛИ-НЕ), 546ЛЕ10 (3ИЛИ-НЕ), 564ЛН2 (инверторы) и 5464ЛА10. Схема показана на рисунке 3.6
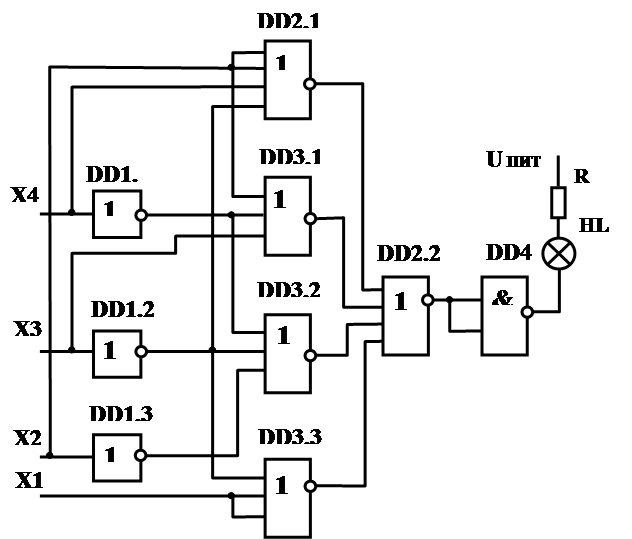
DD1 К564ЛН2
DD2 К564ЛЕ6
DD3 К564ЛЕ10
DD4 К564ЛА10
Рисунок 2.6
Похожие материалы
... 1 На основе полученных логических выражений и синтезированной схемы можно получить логическое выражение и схему для i-го триггера. Di = SL/R* Qi - 1 SL/R* Qi + 1 На основе полученного выражения можно построить схему заданного регистра. Задача№2 Синтез асинхронного двоичного счётчика, выполняющего прямой счёт, с модулем счёта равным 26, используя ...
... 1 1 0 1 0 0 14 1 1 1 0 0 0 15 1 1 1 1 0 1 Для выполнения синтеза логической схемы необходимо произвести следующие действия: 1.по таблице истинности составить логические уравнения для каждого выхода в виде СДНФ и СКНФ; 2.для получения наиболее простой логической схемы выполнить минимизацию функций, записанных в СДНФ и СКНФ, используя метод непосредственных преобразований; 3. ...
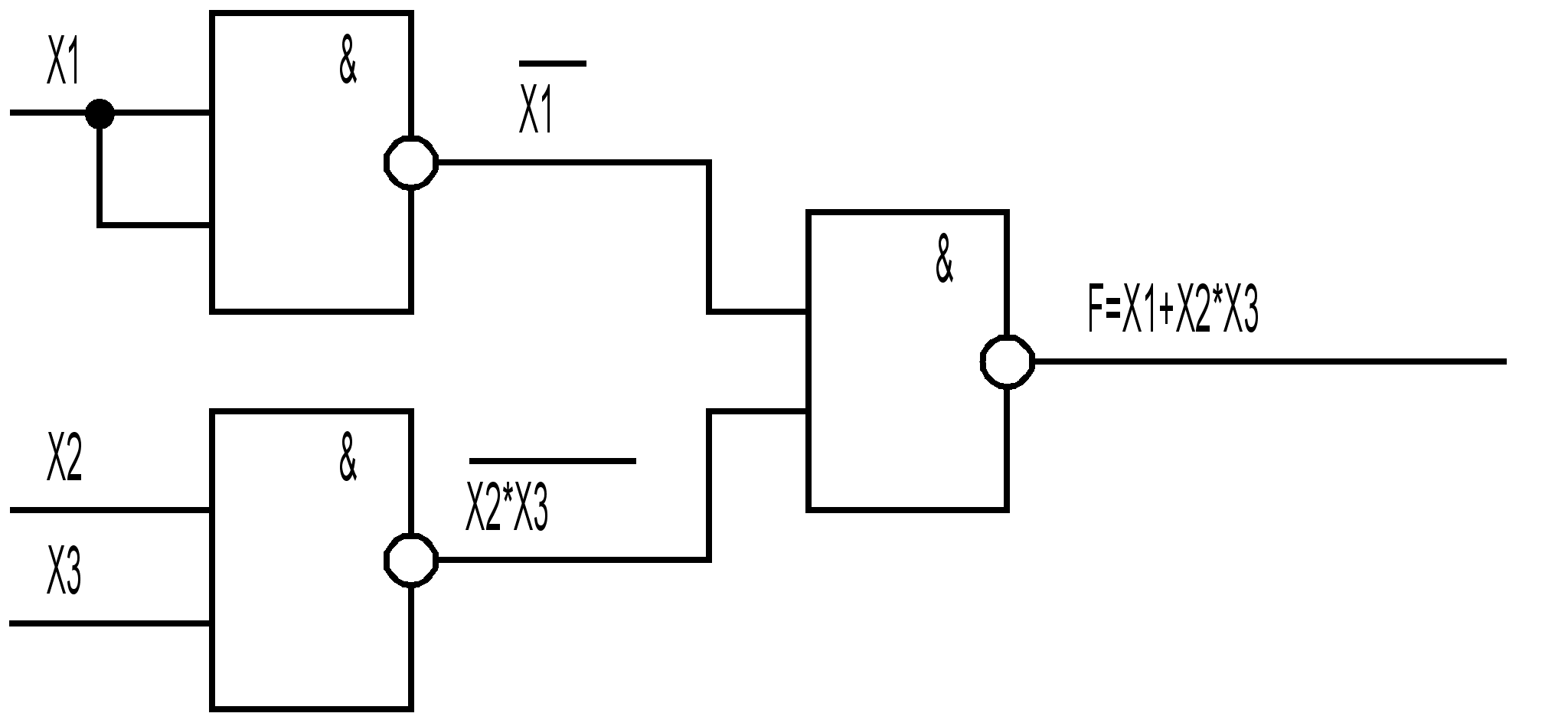
... : студент группы 8033у __________ А.А. Шишков Проверил: к.т.н., доцент кафедры ФТТМ ______________ М.Н. Петров2000 Синтез принципиальной электрической схемы. Исходя из технический параметров ИМС приведенных в ТЗ реализуем логическую функцию F=X1+X2X3 на основе логической схемы ТТЛШ (на логическом базисе 2И-НЕ). Рисунок 1 – Схема логической функции в базисе 2И-НЕ Таблица 1 – ...

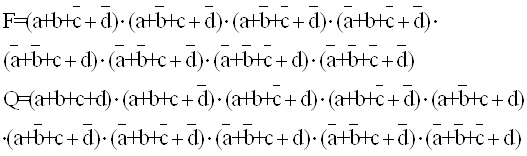

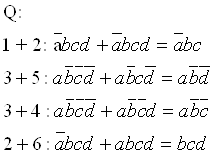
0 комментариев