Аналитическое выражение функции можно составить непосредственно из таблицы истинности. Чтобы формализовать этот процесс, требуется ввести некоторые понятия.
Элементарной (простой) конъюнкцией является конъюнкция, в которой каждая переменная с отрицанием или без отрицания встречается не более одного раза. Отрицание группы переменных отсутствует.
Например:
![]() ,
, ![]() ,
,
Элементарной (простой) дизъюнкцией является дизъюнкция, в которой каждая переменная с отрицанием или без отрицания встречается не более одного раза. Отрицание группы переменных отсутствует.
Например:
![]() ,
, ![]()
Минтермом (конституентой единицы) называется элементарная конъюнкция, которая содержит все используемые в данном случае переменные.
Например, если используются три переменные, то минтермами являются конъюнкции
![]() ,
,![]() ,
,
но конъюнкции
![]() ,
, ![]()
минтермами не являются.
Минтерм равен 1 только для одной комбинации переменных.
Минтерм обозначается символом К i , где i - индекс, который однозначно отождествляется с аналитическим выражением минтерма (конъюнкцией). Зная индекс минтерма, можно определить его аналитическое выражение, и наоборот.
Если задан индекс минтерма, то он записывается в двоичном коде. Затем в каждом разряде 1 заменяются переменными без инверсии, а 0 переменными с инверсией. Причем при замене должно соблюдаться соответствие старшинства переменных старшинству (позициям) разрядов двоичного кода.
Например, требуется получить аналитическое выражение минтерма К6 для трех переменных. Переменные имеют обозначение Х3, Х2, Х1 . .Чем больше номер, тем старше переменная.
Индекс данного минтерма - 6. Число 6 в двоичном коде имеет вид 110. Старший разряд первый слева. Значит в аналитическом выражении минтерма переменные Х3 и Х2 будут без инверсии, а переменная Х1 с инверсией.
Можно использовать следующий алгоритм определения аналитического выражения минтерма. Записываются переменные в порядке старшинства, а под ними записывается двоичный код числа 6 с соблюдением старшинства позиций:
Х3 |
Х2 |
Х1 |
1 |
1 |
0 |
Те переменные, под которыми стоит 0, и будут входить в аналитическое выражение минтерма с инверсией. Таким образом, аналитическое выражение минтерма с индексом 6 для трех переменных:
К 6 = ![]()
Если задано аналитическое выражение минтерма, то в этом выражении переменные без инверсии заменяются 1, а переменные с инверсией 0. Полученное выражение в двоичном коде является индексом минтерма. Двоичное число переводится в десятичное.
Например, требуется определить индекс минтерма ![]() . Переменная Х3 с инверсией, значит, она заменяется 1, остальные переменные заменяются 0.
. Переменная Х3 с инверсией, значит, она заменяется 1, остальные переменные заменяются 0.
Можно использовать следующий алгоритм определения индекса минтерма. Записывается минтерм, и под каждой переменной этого минтерма записывается 0 или 1 в зависимости от того, с инверсией данная переменная или нет.
0 |
1 |
1 |
0112 = 3 |
Полученное под минтермом двоичное число переводится в десятичное. Таким образом, индекс минтерма ![]() - 3.
- 3.
Макстермом (конституентой нуля) называется элементарная дизъюнкция, которая содержит все используемые в данном случае переменные.
Например, если используются три переменные, то макстермами являются дизъюнкции
![]() ,
, ![]() ,
,
но дизъюнкции
![]() ,
, ![]()
макстермами не являются.
Макстерм равен 0 только для одной комбинации переменных.
Макстермобозначается символом Мi , где i - индекс, который однозначно отождествляется с аналитическим выражением макстерма (дизъюнкцией). Зная индекс макстерма, можно определить его аналитическое выражение, и наоборот.
Если задан индекс макстерма, то он записывается в двоичном коде. Затем в каждом разряде 1 заменяются переменными с инверсией, а 0 переменными без инверсии. Причем при замене должно соблюдаться соответствие старшинства переменных старшинству (позициям) разрядов двоичного кода.
Например, требуется получить аналитическое выражение макстерма М6 для трех переменных. Переменные имеют обозначение Х3, Х2, Х1 . .Чем больше номер, тем старше переменная.
Индекс данного макстерма - 6. Число 6 в двоичном коде имеет вид 110. Старший разряд первый слева. Значит в аналитическом выражении макстерма переменная Х1 будет без инверсии, а переменные Х3 и Х2 будут с инверсией.
Можно использовать следующий алгоритм определения аналитического выражения макстерма. Записываются переменные в порядке старшинства, а под ними записывается двоичный код числа 6 с соблюдением старшинства позиций:
Х3 |
Х2 |
Х1 |
1 |
1 |
0 |
Те переменные, под которыми стоит 1, и будут входить в аналитическое выражение макстерма с инверсией. Таким образом, аналитическое выражение макстерма с индексом 6 для трех переменных:
М 6 = ![]()
Если задано аналитическое выражение макстерма, то в этом выражении переменные без инверсии заменяются 0, а переменные с инверсией 1. Полученное выражение в двоичном коде является индексом минтерма. Двоичное число переводится в десятичное.
Например, требуется определить индекс макстерма ![]() . Переменная Х3 с инверсией, значит, она заменяется 1, остальные переменные заменяются 0.
. Переменная Х3 с инверсией, значит, она заменяется 1, остальные переменные заменяются 0.
Можно использовать следующий алгоритм определения индекса макстерма. Записывается макстерм, и под каждой переменной этого макстерма записывается 1 или 0 в зависимости от того, с инверсией данная переменная или нет.
1 |
0 |
0 |
1002 = 4 |
Полученное под макстермом двоичное число переводится в десятичное. Таким образом, индекс макстерма ![]() - 4.
- 4.
Одна и та же логическая функции может быть представлена различными эквивалентными формами.
Если функция представлена в виде дизъюнкции простых конъюнкций, то такая форма представления называется дизъюнктивной нормальной формой (ДНФ).
Например:
![]()
Если функция представлена в виде конъюнкции простых дизъюнкций, то такая форма представления называется конъюнктивной нормальной формой (КНФ).
Например:
![]()
Любая логическая функция может иметь несколько представлений в виде днф и кнф.
Форма представления функции в виде дизъюнкции минтермов называется совершенной дизъюнктивной нормальной формой (СДНФ).
Например:
![]()
Форма представления функции в виде конъюнкции макстермов называется совершенной конъюнктивной нормальной формой (СКНФ).
Например:
![]()
Представление функции в СДНФ или СКНФ единственно.
Любую функцию можно преобразовать в днф и кнф, или в Сднф и Скнф, используя аксиомы и теоремы алгебры логики.
По таблице истинности аналитическое выражение логической функции составляется в СДНФ или СКНФ.
При составлении функции в СДНФ - это дизъюнкция минтермов, при которых функция равна 1. Индексы минтермов соответствуют номерам строк, в которых находятся 1.
При составлении функции в СКНФ - это конъюнкция макстермов, при которых функция равна 0. Индексы макстермов соответствуют номерам строк, в которых находятся 0.
Номер строки в таблице истинности в двоичном коде выражает комбинация переменных, находящаяся в данной строке. Надо только поставить в соответствие старшинство переменных и расположение столбцов в таблице истинности. Старшая переменная должна размещаться в левом крайнем столбце.
Например, логическая функция задана следующей таблицей истинности:
Таблица 1.6
|
Номер строки |
Переменные |
Функция |
||
|
Х 3 |
Х 2 |
Х 1 |
f (ν) |
|
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
2 |
0 |
1 |
0 |
1 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
0 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
0 |
Запись логической функции в СДНФ. Функция равна 1 в четырех случаях, и значит выражение функции будет содержать 4 минтерма. Индексы этих минтермов 1, 2, 3, 6, т.к. единицы находятся в строках с такими номерами. Минтермы записываются по приведенным выше правилам. В результате получится следующее выражение (цифры над минтермами выражают индекс минтерма в двоичном коде и показывают, какие переменные должны быть с инверсией, а какие без инверсии):
![]()
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
![]()
Запись логической функции в СКНФ. Функция равна 0 в четырех случаях, и значит выражение функции будет содержать 4 макстерма. Индексы этих макстермов 0, 4, 5, 7, т.к. нули находятся в строках с такими номерами. Макстермы записываются по приведенным выше правилам. В результате получится следующее выражение (цифры над макстермами выражают индекс макстерма в двоичном коде и показывают, какие переменные должны быть с инверсией, а какие без инверсии):
![]()
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
![]()
Похожие материалы
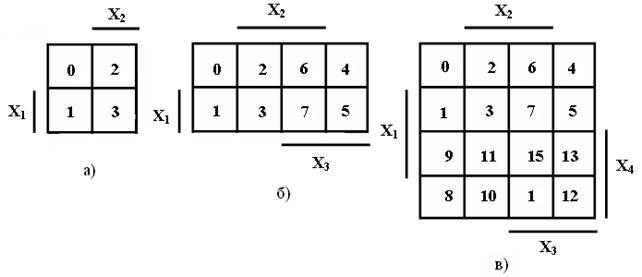
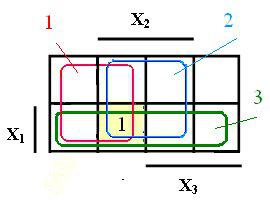
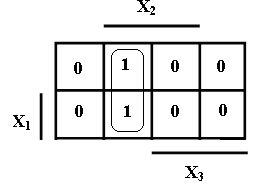
... на рисунке 1 для двух переменных а), трех переменных б) и четырех переменных в). Принципиального значения не имеет, каким вариантом изображения карты Карно пользоваться. В дальнейшем для минимизации используются карты Карно, представленные на рисунке 1 и студентам рекомендуется тоже их использовать. В картах Карно, показанных на рисунке 1, области, где переменные находятся без инверсий (X i), ...
... истинности включает в себя один столбец с номерами строк (он не обязателен и может отсутствовать), столбцы с переменными, (их количество равно количеству переменных), Столбцы с функциями (их количество равно числу выходов логической функции). Полная таблица истинности содержит 2n строк, где n число переменных. Строки в таблице истинности нумеруются, начиная с нуля. Комбинации переменных в ...
... чертеж или схема выполняются в САПР AutoCAD, поэтому наиболее часто используемой вспомогательной программой является конвертор из формата P-CAD в AutoCAD. 1. Основы математического аппарата анализа и синтеза комбинационных логических устройств Все устройства, оперирующие с двоичной информацией, подразделяются на два класса: - комбинационные (дискретные автоматы без памяти). - ...
... X3X4 V X1X2X4 V X1X2X4. Дальнейшее преобразование невозможно. Полученную функцию можно немного упростить с помощью вынесения за скобки общих переменных. 1.3.2 Метод Квайна При минимизации по методу Квайна предполагается, что минимизируемая логическая функция задана в виде ДСНФ. Здесь используется закон неполного склеивания. Минимизация проводится в два этапа: нахождение простых импликант, ...
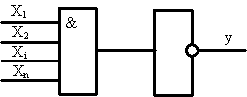
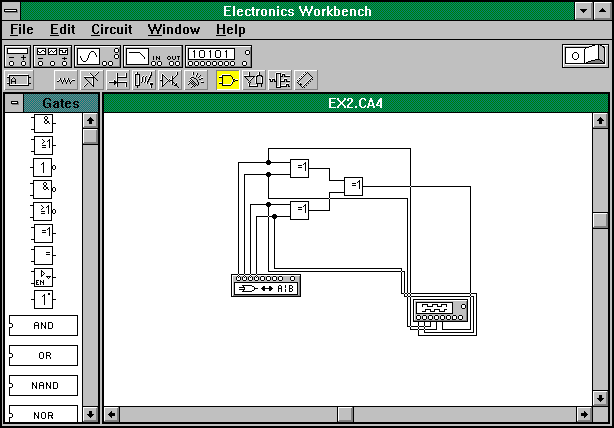
... И-НЕ. Для выполнения этой операции (при имеющемся в окошке булевом выражении) следует “нажать” стрелкой кнопку: 3. Математические модели и эквивалентные схемы в программе логического проектирования Любой реальный логический элемент(ЛЭ) не мгновенно реагирует на изменения входных сигналов, поэтому имеется некоторая паразитная задержка между моментом времени, в который на его входы поступают новые ...
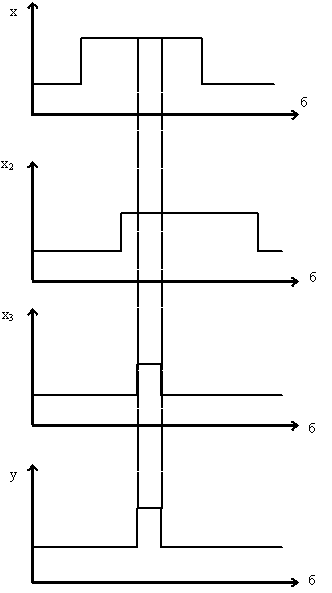
0 комментариев