Простейшими логическими функциями называют функции одной и двух переменных. Число различных значений функций равно 2 m , где m в свою очередь равно 2 n ( n – число переменных). Таким образом, число возможных функций для одной переменной – 4, а для двух переменных – 16. Все они имеют названия и представлены в таблицах 1 и 2.
Таблица 1 Функции одной переменной
|
Х |
0 |
1 |
Аналитическое выражение |
Название функции |
|
f (ν) 1 |
0 |
0 |
0 |
Постоянный 0 |
|
f (ν) 2 |
0 |
1 |
Х |
Повторение Х |
|
f (ν) 3 |
1 |
0 |
|
Отрицание Х |
|
f (ν) 4 |
1 |
1 |
1 |
Постоянная 1 |
Таблица 2 Функции двух переменных
|
Х 1 |
0 |
1 |
0 |
1 |
Аналитическое |
Название функции |
|
Х 2 |
0 |
0 |
1 |
1 |
||
|
f (ν) 1 |
0 |
0 |
0 |
0 |
0 |
Постоянный 0 |
|
f (ν) 2 |
0 |
0 |
0 |
1 |
Х 2 • Х 1 |
Конъюнкция |
|
f (ν) 3 |
0 |
0 |
1 |
0 |
Х 2 |
Запрет по Х 1 |
|
f (ν) 4 |
0 |
0 |
1 |
1 |
Х 2 |
Тождественность Х 2 |
|
f (ν) 5 |
0 |
1 |
0 |
0 |
|
Запрет по Х 2 |
|
f (ν) 6 |
0 |
1 |
0 |
1 |
Х 1 |
Тождественность Х 2 |
|
f (ν) 7 |
0 |
1 |
1 |
0 |
Х 2 (+) Х 1 |
Неравнозначность |
|
f (ν) 8 |
0 |
1 |
1 |
1 |
Х 2 V Х 1 |
Дизъюнкция |
|
f (ν) 9 |
1 |
0 |
0 |
0 |
Х 2 ↓ Х 1 |
Стрелка Пирса |
|
f (ν) 10 |
1 |
0 |
0 |
1 |
Х 2 ~ Х 1 |
Равнозначность |
|
f (ν) 11 |
1 |
0 |
1 |
0 |
|
Отрицание Х 1 |
|
f (ν) 12 |
1 |
0 |
1 |
1 |
Х 2 -> Х 1 |
Импликация от Х 2 к Х 1 |
|
f (ν) 13 |
1 |
1 |
0 |
0 |
|
Отрицание Х 2 |
|
f (ν) 14 |
1 |
1 |
0 |
1 |
Х 1-> Х 2 |
Импликация от Х 1 к Х 2 |
|
f (ν) 15 |
1 |
1 |
1 |
0 |
Х 2 / Х 1 |
Штрих Шеффера |
|
f (ν) 16 |
1 |
1 |
1 |
1 |
1 |
Постоянная 1 |
В практике используются не все функции одной и двух переменных. Достаточно всего несколько, чтобы реализовать сколь угодно сложную схему.
Кроме того, одни функции можно выразить через другие, используя законы, тождества и теоремы алгебры логики. Рассмотрим более подробно простейшие функции, которые реализованы в интегральном исполнении и имеются в языках программировании микропроцессоров и микроконтроллеров.
Отрицание (инверсия, функция НЕ). Обозначается чертой над переменными. Таблица истинности, аналитическое выражение и условное графическое изображение представлены на рисунке 1
|
Номер строки |
Х |
f (ν) |
|
0 |
0 |
1 |
|
1 |
1 |
0 |
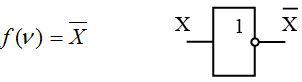
Рисунок 1
Словесное описание: функция принимает инверсное (противоположное) значение переменной.
Конъюнкция ( логическое умножение, функция И). Обозначается символом • между переменными ( используются также символы & и ^ ). Таблица истинности, аналитическое выражение и условное графическое изображение представлены на рисунке 2
|
Номер строки |
Х 2 |
Х 1 |
f (ν) |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
2 |
1 |
0 |
0 |
|
3 |
1 |
1 |
1 |
f (ν) = Х 2 • Х 1
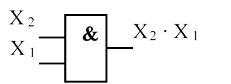
Рисунок 2
Словесное описание: функция принимает единичное значение только тогда, когда все переменные равны единице.
Дизъюнкция (логическое сложение, функция ИЛИ). Обозначается символом V между переменными ( используется также символ + ). Таблица истинности, аналитическое выражение и условное графическое изображение представлены на рисунке 3
|
Номер строки |
Х 2 |
Х 1 |
f (ν) |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
2 |
1 |
0 |
1 |
|
3 |
1 |
1 |
1 |
f (ν) = Х 2 V Х 1
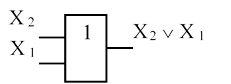
Рисунок 3
Словесное описание: функция принимает единичное значение, если хотя бы одна переменная равна единице.
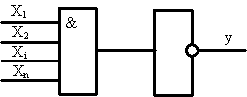
Конъюнкция с отрицанием (логическое умножение с отрицанием, функция И-НЕ). Обозначается символом • между переменными и над выражением ставится черта ( используются также символы & и ^ ). Таблица истинности, аналитическое выражение и условное графическое изображение представлены на рисунке 4.
|
Номер строки |
Х 2 |
Х 1 |
f (ν) |
|
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
2 |
1 |
0 |
1 |
|
3 |
1 |
1 |
0 |
![]()
f(ν) = Х 2 • Х 1 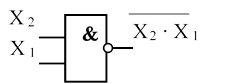
Рисунок 4
Словесное описание: функция принимает единичное значение, если хотя бы одна переменная равна нулю.
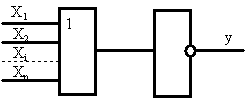
Дизъюнкция с отрицанием (логическое сложение с отрицанием, функция ИЛИ-НЕ).Обозначается символом V между переменными и над выражением ставится черта ( используется также символ + ). Таблица истинности, аналитическое выражение и условное графическое изображение представлены на рисунке 5.
|
Номер строки |
Х 2 |
Х 1 |
f (ν) |
|
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
2 |
1 |
0 |
0 |
|
3 |
1 |
1 |
0 |
![]()
f (ν) = Х 2 V Х 1
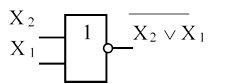
Рисунок 5
Словесное описание: функция принимает единичное значение только тогда, когда все переменные равны нулю.
Неравнозначность (исключающее ИЛИ). Обозначается символом (+) между переменными. Таблица истинности, аналитическое выражение и условное графическое изображение представлены на рисунке 6.
|
Номер строки |
Х 2 |
Х 1 |
f (ν) |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
2 |
1 |
0 |
1 |
|
3 |
1 |
1 |
0 |
f (ν) = Х 2 (+) Х 1
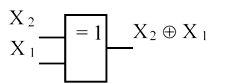
Рисунок 6
Словесное описание: функция принимает единичное значение, тогда, когда только одна переменная равна единице. Для двух переменных (но только для двух) эта функция отражает математическую операцию сумма по модулю два.
Похожие материалы
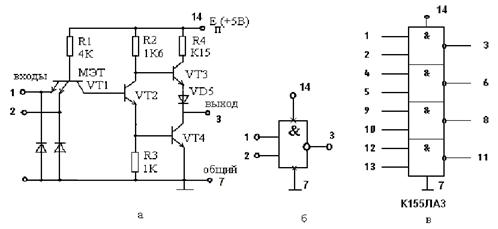
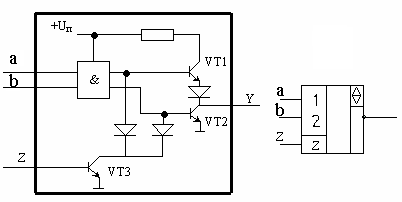
осхемы К155ЛА3 (4 логических элемента 2И-НЕ). Принцип работы ЛЭ И-НЕ ТТЛ Основная особенность микросхем ТТЛ состоит в том, что во входной цепи используется специфический интегральный прибор – многоэмиттерный транзистор (МЭТ), имеющий несколько эмиттеров, объединенных общей базой. Эмиттеры расположены так, что непосредственное взаимодействие между ними через участок базы отсутствует. Поэтому МЭТ ...
... — f(x1,x2,x3,x4) = 3-йэтап—f(x1,x2,x3,x4)= что и требовалось получить. Проверить правильность проведенных преобразований можно при помощи правила склеивания. 3. Функционально полные системы логических функций. Анализ принадлежности переключательных функций замкнутым классам показывает, что существуют две переключательные функции f8 и f14, не принадлежащие ни одному классу. Согласно теореме ...
... чертеж или схема выполняются в САПР AutoCAD, поэтому наиболее часто используемой вспомогательной программой является конвертор из формата P-CAD в AutoCAD. 1. Основы математического аппарата анализа и синтеза комбинационных логических устройств Все устройства, оперирующие с двоичной информацией, подразделяются на два класса: - комбинационные (дискретные автоматы без памяти). - ...
... что знак конъюнкции, как правило, опускается). Предыдущая формула приводит к важной теореме. Теорема. Всякая логическая функция может быть представлена булевой формулой, то есть как суперпозиция конъюнкции, дизъюнкции и отрицания. Действительно, для всякой функции, кроме константы 0, таким представлением может служить её СДНФ. Константу 0 можно представить булевой формулой Ø xx. А почему ...
... X3X4 V X1X2X4 V X1X2X4. Дальнейшее преобразование невозможно. Полученную функцию можно немного упростить с помощью вынесения за скобки общих переменных. 1.3.2 Метод Квайна При минимизации по методу Квайна предполагается, что минимизируемая логическая функция задана в виде ДСНФ. Здесь используется закон неполного склеивания. Минимизация проводится в два этапа: нахождение простых импликант, ...
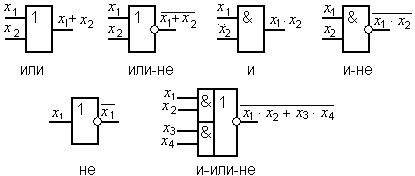
0 комментариев