Совокупность правил записи чисел с помощью ограниченного набора символов называют системой счисления. Системы счисления делятся на позиционные и непозиционные. Примером непозиционной системы может служить система, которую применяли римляне для обозначения чисел.
В позиционной системе счисления количество используемых символов равно основанию системы. Вес (значимость) каждого символа кратен основанию системы и зависит от занимаемой позиции данного символа в записанном числе. Номер позиции символа называют разрядом.
Позиционная система счисления очень удобна для выполнения различных арифметических операций (сложение, вычитание, умножение, деление), поэтому она является основной в цифровой и вычислительной технике.
В общем случае n-разрядное положительное число N в позиционной системе счисления с основанием представляется выражением
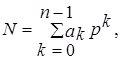 (1.1)
(1.1)
где ak - один из символов используемой системы, значения которых равны членам натурального ряда в диапазоне от 0 до (р – 1), р – основание системы счисления, k – номер позиции (разряда) символа в числе, начиная с 0, p k – весовой коэффициент.
В цифровых устройствах промышленной электроники, микропроцессорной техники и автоматики наиболее часто приходится иметь дело с позиционными системами счисления с основанием 2, 10, 16.
Обработка информации в цифровых устройствах и микропроцессорных устройствах ведется в позиционной двоичной (с основанием 2) системе счисления.
Чтобы отличить двоичное число от чисел, представленных в другой системе счисления, его дополняют справа суффиксом В (Binaire), или снабжают индексом 2.
Для более компактного представления двоичного числа часто используется шестнадцатеричная позиционная система счисления. В этой системе используют первые десять членов натурального ряда от 0 до 9, и первые шесть латинских букв от А до F (A = 10, B = 11, C = 12, D = 13, E = 14, F = 15). Чтобы отличить шестнадцатеричное число от чисел, представленных в другой системе счисления, его дополняют справа суффиксом Н (Hexadecima), или снабжают индексом 16.
Соответствие чисел различных систем счисления представлено в таблице 1.1
Таблица 1.1 Соответствие чисел различных систем счисления
|
Десятичное число |
Шестнадцатеричное число |
Двоичное число |
|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
0 1 2 3 4 5 6 7 8 9 A B C D E F |
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
В позиционных системах счисления перевод целых чисел из системы с любым основанием в десятичную систему осуществляется по формуле (1.1). Например, для преобразования двоичного числа 1010112 в десятичное при формальной подстановке значений в формулу 1.1 получается
1010112 = 1·2 5 + 0·2 4 + 1·2 3 + 0·2 2 + 1·2 1 + 1·2 0 =
=1·32 + 0·16 + 1·8 +0·4 + 1·2 + 1·1 = 32 + 8 + 2 + 1 = 4310
Для перевода чисел из любой позиционной системы в десятичную удобно использовать понятие “весовой коэффициент”. Из формулы (1.1), а также из приведенного примера следует, что весовые коэффициенты двоичного числа, выраженные в десятичном эквиваленте, представляют последовательность чисел: 2 k– 1…, 32, 16, 8, 4, 2, 1.
При переводе двоичного числа в десятичное складываются весовые коэффициенты тех разрядов, значение которых равно единице. Например, при переводе двоичного числа 1010112 в десятичное, подставляя над разрядами двоичного числа соответствующие ему десятичные весовые коэффициенты, получим:
32 16 8 4 2 1
1 0 1 0 1 1
Единица находится в разрядах 0,1,3,5 (счет разрядов начинается с младшего, нулевого), поэтому складываются весовые коэффициенты разрядов 0,1,3,5, т. е. 1 + 2 + 8 + 32 = 43.
Для облегчения перевода желательно знать наизусть десятичные значения чисел 2n от n = 0 до n = 14. Эти значения представлены в таблице 1.2.
Таблица 1.2 Весовые коэффициенты разрядов двоичного числа
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
2 n |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
2048 |
4096 |
8192 |
16384 |
Перевод чисел из десятичной системы в другую позиционную систему осуществляется путем последовательного деления десятичного числа на основание этой системы. Результатом перевода будут остатки, полученные в процессе деления и записанные, начиная с самого последнего. Старшим разрядом полученного числа будет результат последнего деления.
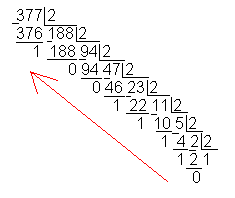
Пример перевода десятичного числа 43 в двоичное:
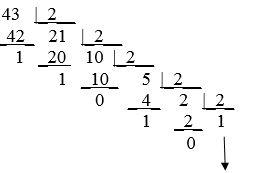
Результат перевода: 43 10 = 101011 2
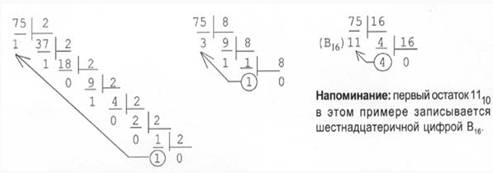
Пример перевода десятичного числа 43 в шестнадцатеричное:
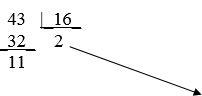
Результат перевода 43 10 = 2В 16 ,так как 1110 = В16,
Шестнадцатеричная система позволяет компактно представлять двоичные числа. Причем перевод из шестнадцатеричной системы в двоичную (и наоборот) осуществить проще и быстрее, чем перевод из десятичной системы в двоичную.
При переводе двоичное число разбивают на тетрады (группы из четырех разрядов), начиная с младшего разряда. Старшую группу при необходимости дополняют до тетрады, дописывая впереди двоичного числа нули. Полученные тетрады представляют разряды шестнадцатеричного числа, и поэтому при переводе двоичная тетрада заменяется соответствующим ей шестнадцатеричным числа (0000 2 соответствует 016, … 1111 2 соответствует F16). Соответствие двоичных тетрад и шестнадцатеричных чисел представлено в таблице 1.1.
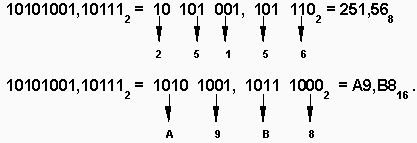
Пример перевода двоичного числа в шестнадцатеричное:
101011 2 = 0010 1011 2 = 2В 16.
2 16 В 16.
Так как 0010 2 = 2 16, а 1011 2 = В 16.
Обратный переход осуществляется аналогично – каждый разряд шестнадцатеричного числа заменяется эквивалентной ему двоичной тетрадой.
Наряду с позиционными системами счисления в цифровых устройствах промышленной электроники, микропроцессорной техники и автоматики используются и непозиционные системы и коды. Наиболее часто используются двоично-десятичная и унитарная системы.
В двоично-десятичной системе счисления число представляет собой последовательность четырехразрядных двоичных комбинаций (тетрад), число которых равно числу разрядов эквивалентного десятичного числа. Каждая двоичная тетрада является двоичным эквивалентом одного разряда десятичного числа. Соответствие двоичных тетрад и десятичных чисел представлено в таблице 1.1. Следует отметить, что численное значение тетрады не может быть больше 9 (в десятичном эквиваленте). Если хотят подчеркнуть, что число двоично-десятичное обычно между тетрадами оставляют пробел, а неполную старшею тетраду дополняют нулями.
Чтобы отличить двоично-десятичное число от чисел, представленных в другой системе счисления, его дополняют справа суффиксом BD (Binary Decimals) или снабжают индексом 2-10.
Пример перевода двоичного числа в десятичное:
101001 2-10 = 0010 1001 2-10 = 29 10
2 10 9 10.
Так как 0010 2 = 2 10, а 1001 2 = 9 10.
Обратный переход осуществляется аналогично – каждый разряд десятичного числа заменяется эквивалентной ему двоичной тетрадой.
В унитарной системе символ 1 находится всегда только в одной позиции, а в остальных позициях находятся 0. Можно сказать, что номер позиции (начиная с 0), где находится 1 это и есть десятичный эквивалент унитарного числа. Нулевой номер правый крайний.
Соответствие чисел унитарной (для восьми разрядов) и десятичной систем счисления представлено в таблице 1.3.
Таблица 1.3 Соответствие чисел унитарной и десятичной систем счисления
|
Десятичное число |
Унитарное число |
|
0 1 2 3 4 5 6 7 |
00000001 00000010 00000100 00001000 00010000 00100000 01000000 10000000 |
Похожие материалы
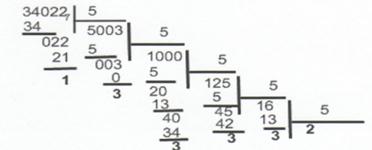
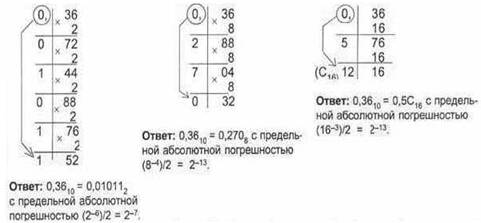
... умножать на основание новой системы счисления до тех пор, пока в новой дроби не будет нужного количества цифр, которое определяется требуемой точностью представления дроби. Правильная дробь в новой системе счисления записывается из целых частей произведений получающихся при последовательном умножении, причем первая целая часть будет старшей цифрой новой дроби. Рассмотрим в качестве примера ...
... представления в них достаточно больших чисел, так как при этом получается чрезвычайно громоздкая запись чисел или требуется очень большой алфавит используемых цифр. В ЭВМ применяют только позиционные системы счисления, в которых количественный эквивалент каждой цифры алфавита зависит не только от вида этой цифры, но и от ее местоположения в записи числа. Позиционные системы счисления В ...
... последовательности 0 и 1. Например целое неотрицательное число А2=Т 111100002 будет храниться в ячейке следующим образом: 1 1 1 1 0 0 0 0 Значит, мы можем записать все числа от 0 до 255 в двоичной системе счисления в 1 ячейке памяти. 2.2 Представление чисел в компьютере Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует ...
... рождения (год, число, месяц). 4. Подведение итогов. Домашнее задание. Учить записи в тетрадях. Заключение В данной курсовой работе было рассмотрена роль и место элективных курсов в предпрофильном обучении, а также разработан элективный курс не тему «система счисления» в предпрофильном обучении информатике. В первой части работы были выявлены главные особенности предпрофильной п
... с основанием p может быть представлено в виде полинома от основания p: N = anpn+an-1pn-1+ ... +a1p+a0+a-1p-1+a-2p-2+ ... (1.1) здесь N – число, aj – коэффициенты (цифры числа), p – основание системы счисления (p>1). Принято представлять числа в виде последовательности цифр: N = anan-1 ... a1a0 . a-1a-2 ... Перевод чисел в десятичную систему осуществляется путем составления степенного ряда ...





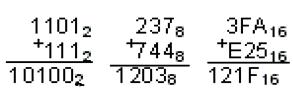
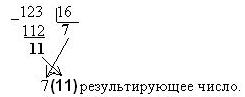
0 комментариев