Теория метода д.ф.-м.н. Юрия Ивановича Виноградова и к.ф.-м.н. Алексея Юрьевича Виноградова решения жестких краевых задач без ортонормирования –
оболочки ракет составные и со шпангоутами.
Идея преодоления трудностей неустойчивого счета путем разделения интервала интегрирования на сопрягаемые участки принадлежит д.ф.-м.н. Юрию Ивановичу Виноградову (в том числе на этом материале защищена докторская диссертация). А выражение идеи разделения и сопряжения через формулы теории матриц, то есть через матричные экспоненты принадлежит к.ф.-м.н. Алексею Юрьевичу Виноградову.
Содержание:
1. Введение. (стр.1-5)
2. Метод решения жестких краевых задач без ортонормирования – метод сопряжения участков, выраженных матричными экспонентами. (стр. 6-7)
3. Составные оболочки вращения. (стр. 8-11) (22 мая 2014)
4. Шпангоут, выражаемый не дифференциальными, а алгебраическими уравнениями. (стр. 10-14) (22 мая 2014)
5. Случай, когда уравнения (оболочки и шпангоута) выражаются не через абстрактные вектора, а через вектора, состоящие из конкретных физических параметров. (стр. 15-17) (22 мая 2014)
Метод решения жестких краевых задач без ортонормирования - оболочки ракет составные и со шпангоутами.
1. Введение.
На примере системы дифференциальных уравнений цилиндрической оболочки ракеты – системы обыкновенных дифференциальных уравнений 8-го порядка (после разделения частных производных методом Фурье).
Система линейных обыкновенных дифференциальных уравнений имеет вид:
![]() ,
,
где ![]() – искомая вектор-функция задачи размерности 8х1,
– искомая вектор-функция задачи размерности 8х1, ![]() – производная искомой вектор-функции размерности 8х1,
– производная искомой вектор-функции размерности 8х1, ![]() – квадратная матрица коэффициентов дифференциального уравнения размерности 8х8,
– квадратная матрица коэффициентов дифференциального уравнения размерности 8х8, ![]() – вектор-функция внешнего воздействия на систему размерности 8х1.
– вектор-функция внешнего воздействия на систему размерности 8х1.
Краевые условия имеют вид:
![]()
где ![]() – значение искомой вектор-функции на левом крае х=0 размерности 8х1,
– значение искомой вектор-функции на левом крае х=0 размерности 8х1, ![]() – прямоугольная горизонтальная матрица коэффициентов краевых условий левого края размерности 4х8,
– прямоугольная горизонтальная матрица коэффициентов краевых условий левого края размерности 4х8, ![]() – вектор внешних воздействий на левый край размерности 4х1,
– вектор внешних воздействий на левый край размерности 4х1,
![]() – значение искомой вектор-функции на правом крае х=1 размерности 8х1,
– значение искомой вектор-функции на правом крае х=1 размерности 8х1, ![]() – прямоугольная горизонтальная матрица коэффициентов краевых условий правого края размерности 4х8,
– прямоугольная горизонтальная матрица коэффициентов краевых условий правого края размерности 4х8, ![]() – вектор внешних воздействий на правый край размерности 4х1.
– вектор внешних воздействий на правый край размерности 4х1.
В случае, когда система дифференциальных уравнений имеет матрицу с постоянными коэффициентами ![]() =const, решение задачи Коши имеет вид [1]:
=const, решение задачи Коши имеет вид [1]:
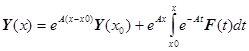 ,
,
где ![]() , где
, где ![]() - это единичная матрица.
- это единичная матрица.
Матричная экспонента ещё может называться матрицей Коши или матрициантом и может обозначаться в виде:
![]() .
.
Тогда решение задачи Коши может быть записано в виде:
![]() ,
,
где 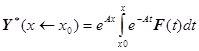 это вектор частного решения неоднородной системы дифференциальных уравнений.
это вектор частного решения неоднородной системы дифференциальных уравнений.
Вместо формулы для вычисления вектора частного решения неоднородной системы дифференциальных уравнений в виде [1]:
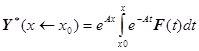
предлагается использовать следующую формулу для каждого отдельного участка интервала интегрирования:
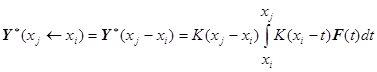 .
.
Вычисление вектора частного решения неоднородной системы дифференциальных уравнений производиться при помощи представления матрицы Коши под знаком интеграла в виде ряда и интегрирования этого ряда поэлементно:
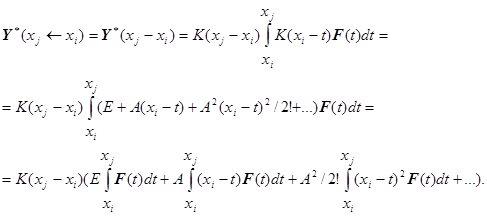
Эта формула справедлива для случая системы дифференциальных уравнений с постоянной матрицей коэффициентов ![]() =const.
=const.
Вектор ![]() может рассматриваться на участке
может рассматриваться на участке ![]() приближенно в виде постоянной величины
приближенно в виде постоянной величины ![]() , что позволяет вынести его из под знака интеграла, что приводит к совсем простому ряду для вычислений на рассматриваемом участке.
, что позволяет вынести его из под знака интеграла, что приводит к совсем простому ряду для вычислений на рассматриваемом участке.
Для случая дифференциальных уравнений с переменными коэффициентами в приведенной выше формуле для каждого участка может использоваться осредненная матрица ![]() коэффициентов системы дифференциальных уравнений.
коэффициентов системы дифференциальных уравнений.
Рассмотрим вариант, когда шаги интервала интегрирования выбираются достаточно малыми, что позволяет рассматривать вектор ![]() на участке
на участке ![]() приближенно в виде постоянной величины
приближенно в виде постоянной величины ![]() , что позволяет вынести этот вектор из под знаков интегралов:
, что позволяет вынести этот вектор из под знаков интегралов:
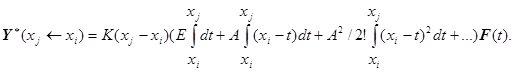
Известно, что при T=(at+b) имеем ![]()
В нашем случае имеем ![]()
Тогда получаем 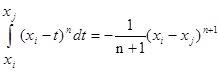 .
.
Тогда получаем ряд для вычисления вектора частного решения неоднородной системы дифференциальных уравнений на малом участке ![]() :
:
![]()
Если участок ![]() не мал, то его можно поделить на подучастки и тогда можно предложить следующие рекуррентные (итерационные) формулы для вычисления частного вектора:
не мал, то его можно поделить на подучастки и тогда можно предложить следующие рекуррентные (итерационные) формулы для вычисления частного вектора:
Имеем ![]() .
.
Также имеем формулу для отдельного подучастка:
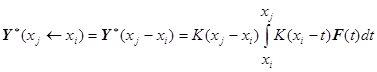 .
.
Можем записать:
![]() ,
,
![]() .
.
Подставим ![]() в
в ![]() и получим:
и получим:
![]()
![]() .
.
Сравним полученное выражение с формулой:
![]()
и получим, очевидно, что:
![]()
и для частного вектора получаем формулу:
![]() .
.
То есть вектора подучастков ![]() не просто складываются друг с другом, а с участием матрицы Коши подучастка.
не просто складываются друг с другом, а с участием матрицы Коши подучастка.
Аналогично запишем ![]() и подставим сюда формулу для
и подставим сюда формулу для ![]() и получим:
и получим:
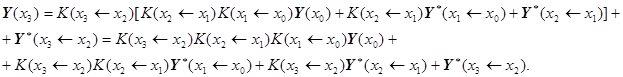
Сравнив полученное выражение с формулой:
![]()
очевидно, получаем, что:
![]()
и вместе с этим получаем формулу для частного вектора:
![]()
То есть именно так и вычисляется частный вектор – вектор частного решения неоднородной системы дифференциальных уравнений, то есть так вычисляется, например, частный вектор ![]() на рассматриваемом участке
на рассматриваемом участке ![]() через вычисленные частные вектора
через вычисленные частные вектора ![]() ,
, ![]() ,
, ![]() соответствующих подучастков
соответствующих подучастков ![]() ,
, ![]() ,
, ![]() .
.
Из теории матриц [Гантмахер] известно свойство перемножаемости матричных экспонент (матриц Коши):
![]()
В случае, когда система дифференциальных уравнений имеет матрицу с переменными коэффициентами ![]() , решение задачи Коши предлагается искать (как это известно) при помощи свойства перемножаемости матриц Коши. То есть интервал интегрирования разбивается на малые участки и на малых участках матрицы Коши приближенно вычисляются по формуле для постоянной матрицы в экспоненте. А затем матрицы Коши, вычисленные на малых участках, перемножаются:
, решение задачи Коши предлагается искать (как это известно) при помощи свойства перемножаемости матриц Коши. То есть интервал интегрирования разбивается на малые участки и на малых участках матрицы Коши приближенно вычисляются по формуле для постоянной матрицы в экспоненте. А затем матрицы Коши, вычисленные на малых участках, перемножаются:
![]() ,
,
где матрицы Коши приближенно вычисляются по формуле:
![]() , где
, где ![]() .
.
2. Метод решения жестких краевых задач без ортонормирования – метод сопряжения участков, выраженных матричными экспонентами.
Разделим интервал интегрирования краевой задачи, например, на 3 участка. Будем иметь точки (узлы), включая края:
![]() .
.
Имеем краевые условия в виде:
![]()
Можем записать матричные уравнения сопряжения участков:
![]() ,
,
![]() ,
,
![]() .
.
Это мы можем переписать в виде, более удобном для нас далее:
![]() ,
,
![]() ,
,
![]() .
.
где ![]() - единичная матрица.
- единичная матрица.
В итоге получаем систему линейных алгебраических уравнений:
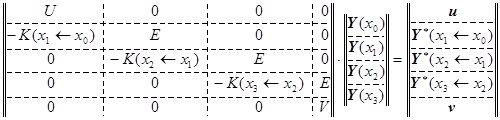 .
.
Эта система решается методом Гаусса с выделением главного элемента.
Оказывается, что применять ортонормирование не нужно, так как участки интервала интегрирования выбираются такой длинны, что счет на них является устойчивым.
В точках вблизи узлов решение находится путем решения соответствующих задач Коши с началом в i-ом узле:
![]() .
.
3. Составные оболочки вращения.
Рассмотрим сопряжения участков составной оболочки вращения.
Пусть имеем 3 участка, где каждый участок может выражаться своими дифференциальными уравнениями и физические параметры могут выражаться по-разному – разными формулами на разных участках:

В общем случае (на примере участка 12) физические параметры участка (вектор ![]() ) выражаются через искомые параметры системы обыкновенных дифференциальных уравнений этого участка (через вектор
) выражаются через искомые параметры системы обыкновенных дифференциальных уравнений этого участка (через вектор ![]() ) следующим образом:
) следующим образом:
![]() ,
,
где матрица ![]() - квадратная невырожденная.
- квадратная невырожденная.
При переходе точки сопряжения можем записать в общем виде (но на примере точки сопряжения ![]() ):
):
![]() ,
,
где ![]() - дискретное приращение физических параметров (сил, моментов) при переходе с участка «01» на участок «12», а матрица
- дискретное приращение физических параметров (сил, моментов) при переходе с участка «01» на участок «12», а матрица ![]() квадратная невырожденная диагональная и состоит из единиц и минус единиц на главной диагонали для установления правильного соответствия принятых положительных направлений сил, моментов, перемещений и углов при переходе с участка «01» на участок «12», которые могут быть разными (в разных дифференциальных уравнениях разных сопрягаемых участков) – в уравнениях слева от точки сопряжения и в уравнениях справа от точки сопряжения.
квадратная невырожденная диагональная и состоит из единиц и минус единиц на главной диагонали для установления правильного соответствия принятых положительных направлений сил, моментов, перемещений и углов при переходе с участка «01» на участок «12», которые могут быть разными (в разных дифференциальных уравнениях разных сопрягаемых участков) – в уравнениях слева от точки сопряжения и в уравнениях справа от точки сопряжения.
Два последних уравнения при объединении образуют уравнение:
![]() .
.
В точке сопряжения ![]() аналогично получим уравнение:
аналогично получим уравнение:
![]() .
.
Если бы оболочка состояла бы из одинаковых участков, то мы могли бы записать в объединенном матричном виде систему линейных алгебраических уравнений в следующей форме:
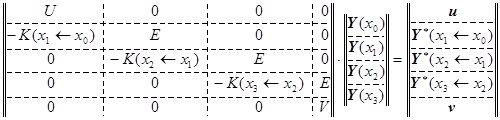 .
.
Но в нашем случае оболочка состоит из 3 участков, где средний участок можно считать, например, шпангоутом, выражаемым через свои дифференциальные уравнения.
Тогда вместо векторов ![]() ,
, ![]() ,
, ![]() ,
, ![]() мы должны рассмотреть вектора:
мы должны рассмотреть вектора:
![]() .
.

Тогда матричные уравнения
![]()
![]() ,
,
![]() ,
,
![]()
примут вид:
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
После перестановки слагаемых получаем:
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В итоге мы можем записать итоговую систему линейных алгебраических уравнений:
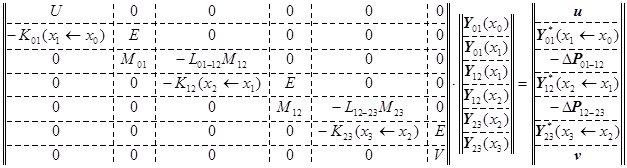
Эта система решается методом Гаусса с выделением главного элемента.
В точках, расположенных между узлами, решение находиться при помощи решения задач Коши с начальными условиями в i-ом узле:
![]() .
.
Применять ортонормирование для краевых задач для жестких обыкновенных дифференциальных уравнений оказывается не надо.
4. Шпангоут, выражаемый не дифференциальными, а алгебраическими уравнениями.
Рассмотрим случай, когда шпангоут (в точке ![]() ) выражается не через дифференциальные уравнения, а через алгебраические уравнения.
) выражается не через дифференциальные уравнения, а через алгебраические уравнения.
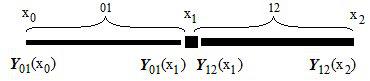
Выше мы записывали, что:
![]()
Можем представить вектор ![]() силовых факторов и перемещений в виде:
силовых факторов и перемещений в виде:
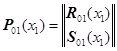 ,
,
где ![]() - вектор перемещений,
- вектор перемещений, ![]() - вектор сил и моментов.
- вектор сил и моментов.
Алгебраическое уравнение для шпангоута:
![]() ,
,
где G – матрица жесткости шпангоута, R – вектор перемещений шпангоута, ![]() – вектор силовых факторов, которые действуют на шпангоут.
– вектор силовых факторов, которые действуют на шпангоут.
В точке шпангоута имеем:
![]() ,
,
то есть нет разрыва в перемещениях ![]() , но есть результирующий вектор силовых факторов
, но есть результирующий вектор силовых факторов ![]() , который складывается из сил и моментов слева плюс сил и моментов справа от точки шпангоута.
, который складывается из сил и моментов слева плюс сил и моментов справа от точки шпангоута.
![]() ,
,
![]() ,
,
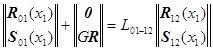 ,
,
![]() ,
,
![]() , где
, где ![]() ,
,
что справедливо, если мы не забываем, что в данном случае имеем:
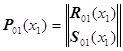 ,
,
то есть вектор перемещений и силовых факторов составляется сначала из перемещений (выше) ![]() , а потом из силовых факторов (ниже)
, а потом из силовых факторов (ниже) ![]() .
.
Здесь необходимо вспомнить, что вектор перемещений ![]() выражается через искомый вектор состояния
выражается через искомый вектор состояния ![]() :
:
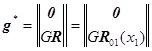 ,
,
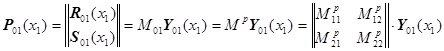 ,
,
где для удобства было введено переобозначение ![]() .
.
Тогда можем записать:
![]() ,
,
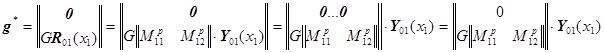
Запишем матричные уравнения для этого случая:
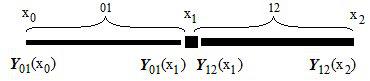
![]()
![]() ,
,
![]() ,
,
![]() .
.
Распишем здесь в уравнении вектор ![]() :
:
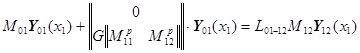 ,
,
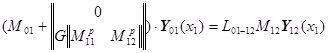 .
.
Для обеспечения негромоздкости введем обозначение:
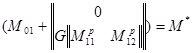 .
.
Тогда уравнение
![]()
примет вид:
![]() .
.
Для удобства переставим слагаемые в матричных уравнениях, чтобы итоговая система линейных алгебраических уравнений записывалась очевидно:
![]()
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, получаем итоговую систему линейных алгебраических уравнений:
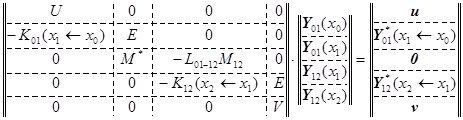 .
.
Если к шпангоуту приложено внешнее силовое-моментное воздействие ![]() , то
, то
![]() следует переписать в виде
следует переписать в виде 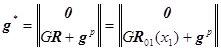 , тогда:
, тогда:
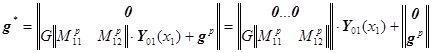 .
.
Тогда матричное уравнение
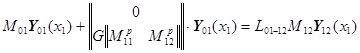
примет вид:
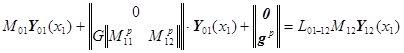 ,
,
![]() .
.
Итоговая система линейных алгебраических уравнений примет вид:
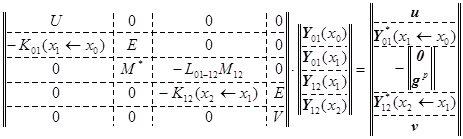 .
.
5. Случай, когда уравнения (оболочки и шпангоута) выражаются не через абстрактные вектора, а через вектора, состоящие из конкретных физических параметров.
Рассмотрим случай, когда части оболочечной конструкции и шпангоут выражаются через вектора состояния (типа ![]() ), которые (в частном случае) совпадают с векторами физических параметров (типа
), которые (в частном случае) совпадают с векторами физических параметров (типа ![]() - перемещения, угол, силы, момент). Тогда матрицы типа
- перемещения, угол, силы, момент). Тогда матрицы типа ![]() будут единичными:
будут единичными: ![]() . И пусть положительные направления физических параметров одинаковы для всех частей оболочки и шпангоута (
. И пусть положительные направления физических параметров одинаковы для всех частей оболочки и шпангоута (![]() ).
).
Тогда будем иметь уравнения:
![]() ,
,
![]() ,
,
![]() ,
,
в виде:
![]() ,
,
![]() ,
,
![]() ,
,
где E – единичная матрица.
Уравнения
![]() ,
,
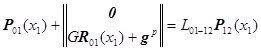 ,
,
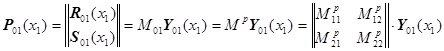 ,
,
![]() ,
,
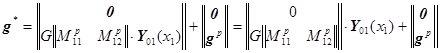 ,
,
примут вид:
![]() ,
,
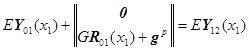 ,
,
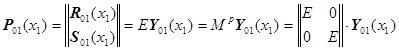 ,
,
![]() ,
,
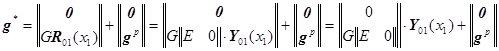 .
.
А уравнения
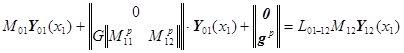 ,
,
![]() .
.
примут вид:
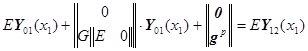 ,
,
![]() , где
, где 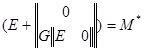
Итоговая система линейных алгебраических уравнений
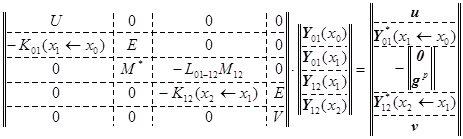
примет вид:
 ,
,
где 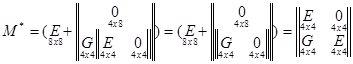 .
.
Это означает, что уравнение
![]()
принимает вид:
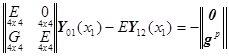
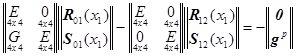
![]() , (нет скачка в перемещениях и угле) и
, (нет скачка в перемещениях и угле) и
![]() - равновесие шпангоута,
- равновесие шпангоута,
то есть:
![]() (перемещения и угол: нет разрыва)
(перемещения и угол: нет разрыва)
![]() , где
, где ![]() (силы и момент: равновесие).
(силы и момент: равновесие).
Похожие материалы
... D2 ∙ c = p. Отсюда получаем, что: c = D2 ∙ ( p - D1∙ u ) Таким образом, искомые константы найдены. Далее показано как применять этот метод для решения «жестких» краевых задач. Запишем V∙ K(1←0) ∙ ∙ = p. совместно с K(1←0) = K(1←x2) ∙ K(x2←x1) ∙ K(x1←0) и получим: V∙ K(1←x2) ∙ K(x2&# ...
... кадрами и т.д. и т.п., иными словами – совер-; Шенствовать системы и процессы государственного управления, восо-|бенности осуществляемого органами исполнительной власти. '. Развитие науки административного права немыслимо без изучения ее истории, ранее применявшегося законодательства, существовавших.Концепций по соответствующим проблемам. Российская наука адми-•нистративного права – одна из первых ...
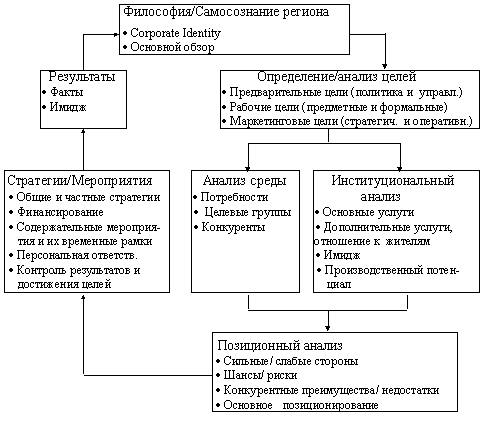
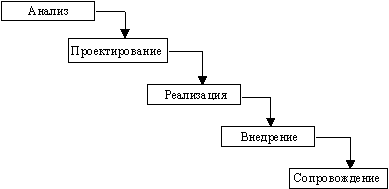
... Architect, Visible Analyst Workbench, EasyCASE), так и новые версии и модификации перечисленных систем. 3 Глава. Разработка концептуальной модели информационной системы для поддержки принятия управленческих решений при формировании маркетинговой стратегии региона Процесс создания и внедрения любой ИС принято разделять на четыре последовательные фазы: анализ, глобальное проектирование ( ...
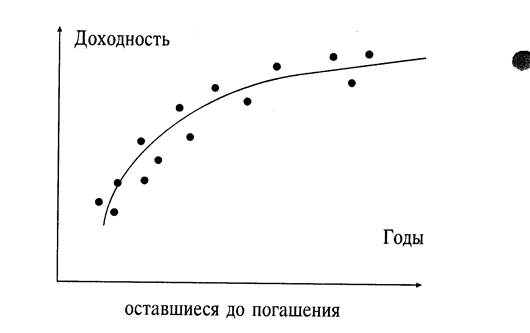
... . 4. Какие основные факторы нужно определить прежде, чем формировать инвестиционный портфель клиента? 5. Опишите простую структуру инвестиционного портфеля. ВВЕДЕНИЕ РАЗВИТИЕ РЫНКА ЦЕННЫХ БУМАГ В РОССИИ И ЗАДАЧИ РЕГУЛИРОВАНИЯ Рынок ценных бумаг в России начал свое формирование в первой половине 1991 г. после принятия известного Постановления Совета министров РСФСР ¹ 601 от 25 ...
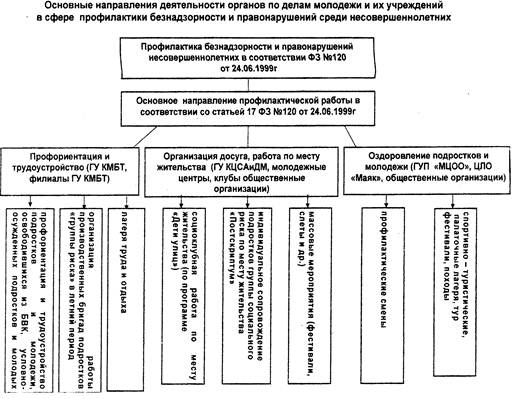
... общегосударственный подход в организации работы с несовершеннолетними группы риска, определены субъекты социальной и профилактической работы. В Федеральном законе "Об основах системы профилактики безнадзорности и правонарушений несовершеннолетних" [ФЗ № 120] определены группы детей – объектов профилактической работы, а именно: Безнадзорный - несовершеннолетний, контроль за поведением которого ...



0 комментариев