Случайные величины и их законы распределения

4. Случайные величины и их законы распределения

Законом распределения СВ называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину будем говорить, что она подчинена данному закону распределения.

Простейшей формой задания закона является табл. 1, в которой перечислены возможные значения СВ и соответствующие им вероятности.

Таблица 1

x1	x2	…	xN
p1	p2	…	pN

Однако такую таблицу невозможно построить для непрерывной СВ, поскольку для нее каждое отдельное значение не обладает отличной от нуля вероятностью.

Для количественной характеристики распределения используют зависимость вероятности события X < x, где x – некоторая текущая переменная, от x. Эта функция называется функцией распределения СВ X и обозначается F(x): F(x) = P(X < x). Функцию распределения F(x) иногда называют интегральной функцией распределения или интегральным законом распределения.

Функция распределения существует для всех СВ – как непрерывных, так и дискретных.

Сформулируем некоторые общие свойства F(x):

1) F(x) есть неубывающая функция своего аргумента, т.е. при x₂ > x₁ F(x₂) > F(x₁);

2) на –¥ F(x) равна нулю, т.е. F(–¥) = 0;

3) F(¥) =

По определению, F(x) при некотором x есть вероятность попадания СВ X в интервал от –¥ до x.

Для дискретной СВ распределение F(x) имеет ступенчатый вид, причем величина каждого скачка равна вероятности значения, при котором имеется скачок F(x).

При решении практических задач часто необходимо вычислять вероятность того, что СВ примет значение, заключенное в некоторых пределах, например от x₁ до x₂. Это событие называется «попаданием СВ X на участок от x₁ до x₂». Выразим вероятность этого события через функцию распределения СВ X. Для этого рассмотрим два события:

– событие А, состоящее в том, что X < x₂;

– событие В, состоящее в том, что X < x₁;

– событие С, состоящее в том, что x₁ < X < x₂.

Учитывая, что А = В + С, по теореме сложения вероятностей получим , или , откуда , т.е. вероятность попадания СВ на заданный участок равна приращению функции распределения на этом участке.

Пусть имеется непрерывная СВ X с функцией распределения F(x), которую считаем непрерывной и дифференцируемой. Вычислим вероятность попадания этой СВ на участок от x до x + Dx: , т.е. эта вероятность равна приращению функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка или среднюю вероятность, приходящуюся на единицу длины на этом участке. Кроме того, устремим Dx к нулю. В пределе получим производную от функции распределения:

.

Обозначим  через f(x). Полученная функция характеризует плотность, с которой распределяется значение СВ в данной точке x. Это и есть плотность вероятности. Иногда ее называют дифференциальным законом распределения СВ X.

Если X есть непрерывная СВ с плотностью вероятности f(x), то величина f(x)dx есть элементарная вероятность, соответствующая событию – попаданию СВ X на отрезок dx. Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок dx и ограниченного сверху функцией f(x).

Свойства плотности вероятности:

1)  при всех x, поскольку вероятность не может быть отрицательной (кроме того, производная неубывающей функции не может быть отрицательной);

2) ;

3) ;

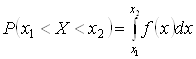4) свойство нормировки 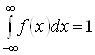, т.е. площадь, ограниченная графиком плотности вероятности и осью x, всегда равна 1 (кроме того, попадание СВ X в неограниченную с обеих сторон ось x является достоверным событием).

Во многих практических ситуациях нет необходимости характеризовать СВ плотностью вероятности. Часто бывает достаточно указать только отдельные числовые параметры, характеризующие в какой-то степени существенные черты распределения СВ, например, среднее значение, вокруг которого группируются возможные значения СВ; число, характеризующее степень разбросанности этих значений относительно среднего значения и т.д. Такие характеристики называются числовыми характеристиками СВ.

Математическое ожидание (МО) иногда называют средним значением СВ. Оно обозначается  и для дискретной СВ определяется по формуле

.

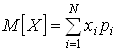Это среднее взвешенное значение и называют МО.

Математическим ожиданием СВ называют сумму произведений всех возможных значений СВ на вероятности этих значений.

Математическое ожидание СВ X связано со средним арифметическим значением наблюдаемых значений СВ при большом числе опытов так же, как и вероятность с частотой события, т.е. при увеличении числа опытов среднее арифметическое значение стремится к МО.

Для непрерывной СВ МО определяется по формуле

.

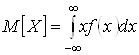Физически МО можно трактовать как координату центра тяжести тела (плотности вероятности). Единица измерения МО соответствует единице измерения СВ.

Моменты. Дисперсия. Среднеквадратическое отклонение. Начальным моментом s-го порядка для дискретной СВ X называется сумма вида 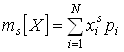. Для непрерывной СВ –

.

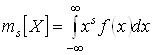Из этих формул видно, что МО есть не что иное, как первый начальный момент СВ X. Условно, используя знак МО, можно записать выражение для s-го начального момента, т.е.  – начальным моментом s-го порядка СВ X называют МО s-й степени этой СВ.

Центрированной СВ, соответствующей СВ X, называют отклонение СВ X от ее МО, т.е. . Нетрудно убедиться, что МО центрированной СВ равно нулю. Моменты центрированной СВ называют центральными моментами. Таким образом, центральным моментом s-го порядка называют МО s-й степени центрированной СВ: . Для непрерывной СВ s-й центральный момент выражают интегралом:

.

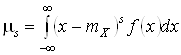Введем соотношения, связывающие центральные и начальные моменты различных порядков: ; ; ;…

Из всех моментов чаще всего в статистической радиотехнике применяют МО и вторые моменты – начальный и центральный. Второй центральный момент называют дисперсией СВ X. Для нее вводят специальное обозначение , или D_X.

Дисперсия характеризует степень разбросанности (или рассеивания) СВ X относительно математического ожидания и имеет размерность квадрата СВ X. На практике удобнее пользоваться величиной, размерность которой совпадает с размерностью СВ. Для этого из дисперсии извлекают квадратный корень. Полученную величину называют среднеквадратическим отклонением (СКО). Ее обозначают через . При извлечении квадратного корня из второго начального момента получается величина, названная среднеквадратическим значением (СКЗ). Часто используют формулу, связывающую основные моменты:

.

Третий центральный момент служит для характеристики асимметрии (или «скошенности») плотности вероятности. Если плотность вероятности симметрична относительно МО, то все моменты нечетного порядка равны нулю. Поэтому естественно в качестве характеристики асимметрии плотности вероятности выбрать какой-либо из нечетных моментов, из них простейший . Но чтобы иметь безразмерную величину, этот момент делят на куб среднеквадратического отклонения . Полученная величина носит название коэффициента асимметрии или просто асимметрии, обозначают ее через S_k:

.

Четвертый центральный момент служит для характеристики так называемой «крутости» (островершинности или плосковершинности) плотности вероятности. Эти свойства распределения описываются с помощью так называемого эксцесса: 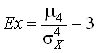. Число 3 вычитается из отношения  потому, что для весьма распространенного в природе нормального закона это отношение равно трем.

Кроме рассмотренных моментов, используют иногда абсолютные моменты (начальные и центральные): ; . Из них чаще всего применяют первый абсолютный центральный момент , называемый средним арифметическим отклонением. Его используют наряду со среднеквадратическим отклонением для характеристики рассеивания СВ, для которых не существует дисперсии.

Кроме таких характеристик, используются понятия мода и медиана плотности вероятности. Модой (М) называют наиболее вероятное значение, соответствующее максимуму плотности вероятности (если таких максимумов несколько, то распределение называют полимодальным). Медиана (Ме) – это такое значение СВ X, для которого P(X < Me) = P(X > Me). В случае симметричного одномодального (унимодального) распределения медиана совпадает с МО и модой.

Распределение Лапласа (двухсторонний экспоненциальный):

,

где m – МО; l – характеризует степень разбросанности X относительно m.

2. Биномиальное распределение (Бернулли):

.

Например, это распределение используется для определения вероятностей правильного обнаружения и ложной тревоги по пачке импульсов при заданных вероятностях обнаружения и вероятности ложной тревоги одного импульса в пачке.