Навигация
Застосування клина та важеля в техніці
План
1. Плоскість похилої, важіль, клин і їх вживання в машинах
2. Рівновага сил на похилій плоскості
3. Золоте правило механіка
4. Важіль, його рівноваги і різновиди
5. Клин і застосування клина в техніці
6. К. К. Д. ворота, блока і поліспасту
Список використаної літератури
1. Плоскість похилої, важіль, клин і їх вживання в машинах
На кордоні піщаної пустелі в Єгипті височіє ступінчаста піраміда Хеопса заввишки 146 м. Вона побудована з плит вагою по 2,5 т кожна. Очевидно, що люди, що зводили подібні споруди, не могли піднімати на висоту такі плити і глиби без елементарних механічних пристосувань, так званих простих механізмів. Одним з цих механізмів є плоскість похилої. Плоскість похилої дозволяє, користуючись малою силою, підняти або опустити великий вантаж. Тому принципи роботи похилої плоскості використовуються в багатьох конструкціях сучасних машин і механізмів, наприклад ланцюгові, стрічкові і канатні транспортери; гвинтове різьблення.
2. Рівновага сил на похилій плоскості
Розглянемо, які сили діють на тіло, поміщене на похилу плоскість АВ, підняту на висоту ВС (мал. 1). Позначимо: ![]() G— вага тіла; P— тягове зусилля; a — кут нахилу плоскості до горизонту; в — кут, утворений тяговим зусиллям з похилою плоскістю; ѓ — коефіцієнт тертя; l — довжина похилої плоскості АВ; h — висота похилої плоскості ВС.
G— вага тіла; P— тягове зусилля; a — кут нахилу плоскості до горизонту; в — кут, утворений тяговим зусиллям з похилою плоскістю; ѓ — коефіцієнт тертя; l — довжина похилої плоскості АВ; h — висота похилої плоскості ВС.
Власна вага тіла G, направлений вертикально вниз, розкладемо на дві складові: G1, паралельну похилій плоскості АВ, і G2, перпендикулярну до неї. Силу G1 знаходимо з подібності трикутників АБС і OG1G:
тобто при користуванні похилою плоскістю ми отримуємо виграш в силі в стільки раз, в скільки разів довжина похилої плоскості більше її висоти. Але відношення
Розглянемо випадок, коли тіло рухається вгору по похилій плоскості. Щоб рівномірно піднімати тіло вгору по похилій плоскості з врахуванням тертя, необхідно прикласти до нього силу, велику G1 на величину сили тертя, тобто має бути дотримане умова
Де F – сила тертя, викликана нормальним тиском N оскільки ![]() то:
то:
![]() .
.
отже: ![]()
Підставляючи в це рівняння значення сил, отримуємо
![]() .і
.і ![]()
Звідси: ![]()
При русі тіла вниз по похилій плоскості напрям сили тертя буде протилежним вказаному на мал. 1, а отже, знак у формулі перед f має бути змінений на зворотний
![]()
4. Золоте правило механіка
Якщо не враховувати силу тертя і опір середовища, то при підйомі тіла вагою G на висоту h здійснюється робота
![]()
при підйомі ж тіла по похилій плоскості здійснюється робота тобто користування похилою п плоскість не дає виграшу в роботі, оскільки в скільки разів ми виграємо в силі, в стільки ж раз програємо у відстані. Це правило справедливо для всіх машин. Воно отримало назву золотого правила механіки.
5. Важіль, його рівноваги і різновиди
Важіль , так само як і плоскість похилої, є простим механізмом, користуючись яким людина з малою силою може зробити велику роботу. Кліщі для витягування цвяхів, тачка, залізничний шлагбаум, підіймальний кран — все це приклади важеля.
У загальному вигляді важіль можна представити як стрижень, що має вісь обертання або точку опори, довкола якої він може обертатися під дією сил.
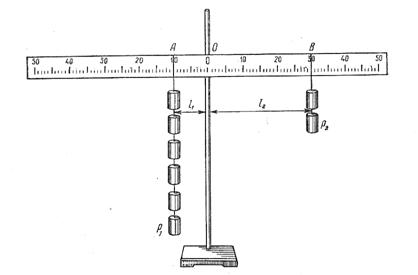
Рівновага вантажів, підвішених по кінцях стрижня, залежить як від їх ваги, так і від відстані до крапки опори стрижня. Очевидно, що два рівні вантажі підвішених на різних відстанях від точки опори, врівноважують одне одного. У тих же умовах більший вантаж переважить менший. Якщо відсовувати менший вантаж вправо (мал. 2), то можна добитися того, що менший вантаж переважить більший.
За яких умов ми доб'ємося виграшу з силі? Позначимо точку опори важеля буквою О, а крапки додатку сил — буквами .А і В. Прямі АР1 і ВР2 — лінії, уздовж яких діють сили Р1 і Р2.
Перпендикуляр, опущений з точки опори важеля на лінію, вздовж якої діє сила, називається плечем сили, або плече сили є найкоротший шлях від точки опори до лінії дії сили . Відстань l1 і l2– плечі сил Р1 і Р2 . Робота сили на плече дає момент сили:
M1=P2 l2; M2P2 l2
(мал. 1)
Важіль буде находитись в рівновазі , коли M1=M2 момент сили ,обертаючи важіль за часовою стрілкою дорівнює моменту сили, обертів важеля проти стрілки P1l1=P2l2.
Користуючись важелем, ми виграємо в силі в стільки раз, в скільки одне плече більше іншого. Ми розглянули важіль, в якого точки додатка сил розташовані: по різні сторони від точки опори. Важелі такого типа прийнято називати важелями першого роду (залізничний шлагбаум). Часто використовуються важелі у яких точки прилягання сил лужать на одну сторону точки опори. Такі важелі називаються важелями другого роду
Похожие работы
... і випадків зміна кінематичної схеми викликало ускладнення як самої схеми, так і конструкції машини. Отримуваний невеликий техніко-економічний ефект не оправдовував ускладнення конструкції і подорожання ремонту. Не оправдавши себе конструкції дробарок, не дивлячись на значне поширення (наприклад, дробарки типу «Додж» і дробарки з кулачковим механізмом), постійно витіснялись більш раціональними ...
... яльність щодо зберігання зерна, міститься інформація про обсяги і рух зерна протягом місяця. Наступним заходом для створення організаційних умов конкурентоспроможного виробництва, формування рівноважного ринку зерна та налагодження діяльності зернопродуктового підкомплексу повинно відбутися врегулювання цін на зерно в післяжнивний період, що характеризується найбільшою диспропорційністю між міні ...
... званого середнього учня; об'єкти мають бути такими, щоб їх міг зробити кожний. По-друге, введення школярів до основ обробки матеріалів має здійснюватися через фронтальну форму організації праці, оскільки, проведення вступних, поточних та заключних інструктажів, аналіз і оцінювання трудових дій п'ятикласників, впровадження елементів само- та взаємоконтролю будуть ефективними саме при такій органі ...
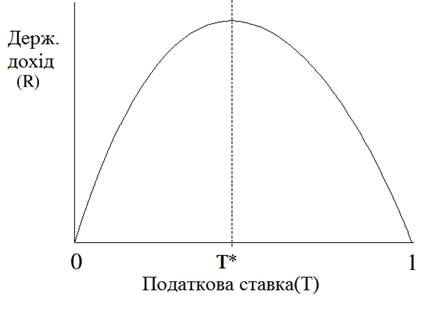
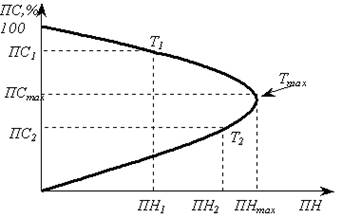
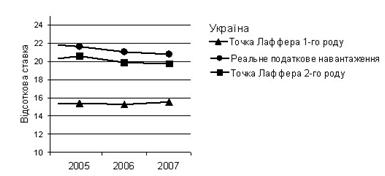
... знайти ту точку на кривій Лаффера, де знаходиться економіка в даний момент; як визначити той оптимальний рівень податкових ставок, який здатний забезпечити максимальну величину податкових находжень. Застосування кривої Лаффера на практиці є певним політичним ризиком, на який політикам слід зважуватись лише за умов, якщо існують тверді переконання, що діючі податкові ставки дійсно є надмірними і ...




0 комментариев