Операторні та предикатні алгоритми -ІІ

4. Операторні та предикатні алгоритми -ІІ

(Рекурсивні функції на областях, що відмінні від N)

Оскільки БРМ працює тільки з натуральними числами, наше визначення обчислюваності і можливості розв'язання застосовано тільки до функцій і предикатів від натуральних чисел. Ці поняття легко поширюються на інші види об'єктів (тобто цілі числа, поліноми, матриці і т.д.) за допомогою кодування.

Кодуванням області D об'єктів називається явне й ефективне відображення α: D →N. Ми будемо говорити, що об'єкт α ? D кодується натуральним числом α (d). Припустимо, що f є функцією з D в D; тоді f природно кодується функцією f* з N в N, що відображає код кожного об'єкта d ? Dom(f) у код об'єкта f (d). У явному виді це можна записати як

f*=α · f ·a^-1

Тепер можна поширити визначення Мнр-обчислюваності на область D, рахуючи функцію f обчислюваною, якщо f^*–обчислювана функція натуральних чисел.

Приклад. Розглянемо область Z. Явне кодування можна задати функцією α, де

2n, якщо n ³ 0,

α^-(n) =

-2n-1, якщо n < 0.

Тоді α^-1 задається так:

(1/2) m, якщо m парне,

α^-1 (m) =

(-1/2) (m+1), якщо m непарне.

Тепер розглянемо функцію х-1 на Z; позначаючи цю функ-ю через f, одержуємо f*:N →N, що задається:

1, якщо x:==0 (тобто х=α(0)),

f^*(x)= х-2, якщо х> 0 і х парне (тобто х=а(п), п>0),

х +2, якщо х непарне (тобто х=α(n), п < 0).

Написання програми, що обчислює f*, є рутинною вправою; отже, х-1 є обчислювана функція на Z.

Приведене вище визначення очевидним образом розширюється на n-місцеві обчислювальні функції на області D і розв'язні предикати на D.

5. Алгоритмічні проблеми для L

Нижче дається огляд нерозв'язних проблем, що виникають у самій теорії обчислювальності, і обговорюються деякі методи доказу нерозв'язності. Нагадаємо, що предикат М(х) називається розв'язним, якщо його характеристична функція, що задається формулою

1, якщо M(x) правдиве,

C_m (x) =

0, якщо M(x) неправдиве

обчислювана. Це рівносильно твердженню про те, що предикат М (х) рекурсивний Предикат М (х) називається нерозв'язним, якщо він не є розв'язним. У літературі використовуються наступні терміни, еквівалентні твердженню про те, що предикат М (х) розв'язний:

М (х) рекурсивний,

М (х) має рекурсивну проблему дозволу,

М (х) рекурсивно розв'язний,

М (х) обчислювальний.

Алгоритм, що обчислює с_м, називається обчислювальною процедурою, для M(x).

1. Нерозв'язні проблеми в теорії обчислюваності

У більшості випадків докази нерозв'язності ґрунтуються на діагональному методі, як, наприклад, у наступному важливому прикладі.

1.1. Теорема. Проблема «x ÎW_x» (чи, що еквівалентно, «функція f_x(х) визначена», чи «Р_x(х)¯», чи «функціяy_u(х, х) визначена») нерозв'язна.

Доведення. Характеристична функція цієї проблеми задається наступною формулою:

1, якщо xÎ W_x

f(x)=0, якщо xÏ W_x

Припустимо, що функція f обчислювана, і приведемо це припущення до протиріччя. Саме за допомогою діагонального методу ми побудуємо обчислювану функцію g, таку, що Dom(g)¹W_x(= Dom(ф_x)), при всіх х, чого, мабуть, бути не може.

Як завжди при використанні діагонального методу, ми будемо прагнути до того, щоб множина Dom(g) відрізнялося від W_x у njxці х. Тому будемо домагатися того, щоб

x Î Dom (g) Ûx ÏW_x

Визначимо тепер функцію g у такий спосіб:

g(x)= 0, якщо xÏ W_x (тобто якщо f(x)=0),

не визначена, якщо xÎ W_x (тобто якщо f(x)= 1).

Оскільки функція f обчислювана, то (по тезі Черча) обчислювана і функція g, що і дає необхідне протиріччя. (Більш докладно, оскільки функція g обчислювана, візьмемо таке т, що g=f_m, тоді т Î W_m Û т Î Dom (g)Ûт Ï W_m, чого не може бути.)

Отже, ми робимо висновок, що функція f не є обчислюваною, і, отже, проблема «x ÎW_x» нерозв'язна. ÿ

Зауважимо, що ця теорема зовсім не затверджує, що ми не можемо для будь-якого конкретного числа а сказати, чи буде визначене значення f_a (a). Для деяких чисел зробити це дуже просто. Наприклад, якщо ми написали програму Р, що обчислює тотальну функцію, і Р=Р_a, то ми відразу знаємо, що значення f_a (a) визначено. Теорема говорить лише, що не існує єдиного загального методу рішення питання про те, чи буде f_x(х) визначено; іншими словами, не існує методу, що працює при всіх х.

Простий наслідок цього результату полягає в наступному.

Похожие работы

Непрерывные генетические алгоритмы

Скачать

33080

5

4

... число эпох функционирования алгоритма, или определение его сходимости, обычно путем сравнивания приспособленности популяции на нескольких эпохах и остановки при стабилизации этого параметра. 3. Непрерывные генетические алгоритмы. Фиксированная длина хромосомы и кодирование строк двоичным алфавитом преобладали в теории генетических алгоритмов с момента начала ее развития, когда были получены ...

Формализация понятия "алгоритм"

Скачать

18213

1

5

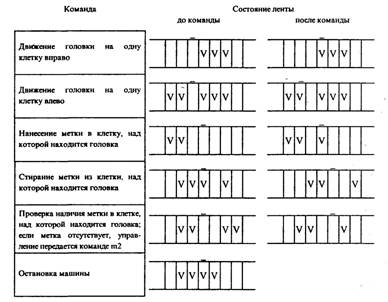
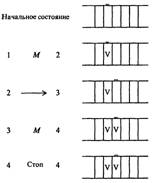
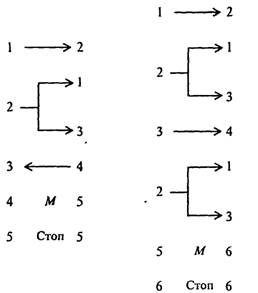
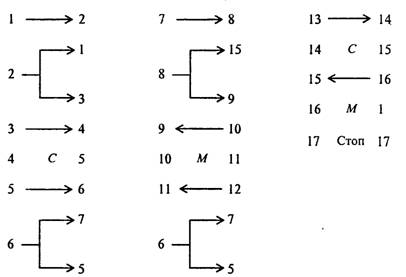
... в состояние qj, заменяя содержимое ячеек соответственно символами аb1 - аbк, то после этого ленты соответственно сдвигаются в направлениях k1... kk. До сих пор принималось, что различные алгоритмы осуществляются на различных машинах Тьюринга, отличающихся набором команд, внутренним и внешним алфавитами. Однако, можно построить универсальную машину Тьюринга, способную выполнять любой алгоритм ...

Быстрые алгоритмы сортировки

Скачать

26020

3

4

... M2(n) = O(l n), C2(n) = O(l n). Оскільки l = log2n, M2(n)=O(n log2 n)), C2(n)=O(n log2 n), Але З(n) = C1(n) + C2(n), M(n) = M1(n) + M2(n). Тому що C1(n) < C2(n), M1(n) < M2(n), остаточно одержуємо оцінки складності алгоритму TreeSort за часом: M(n) = O(n log2 n), C(n) = O(n log2 n), У загальному випадку, коли n не є ступенем 2, сортуюче дерево будується трохи інакше. “Зайвий” елемент ...

Нормальные Алгоритмы Маркова. Построение алгоритмов из алгоритмов.

Скачать

10075

2

1

... U4 сравнения двух целых чисел оставляем читателю в качестве упражнения. Замечание: исходное слово надо задать в форме  * Для нормальных алгоритмов Маркова справедлив тезис, аналогичный тезису Тьюринга. Тезис Маркова: Для любой интуитивно вычислимой функции существует алгоритм, ее вычисляющий. Построение алгоритмов из алгоритмов. До сих пор, строя ту или иную МТ, или НАМ мы каждый раз ...