Навигация
Построение графиков функций. Решение нелинейных уравнений и систем нелинейных уравнений
Введение
Тема контрольной работы «Построение графиков функций. Решение нелинейных уравнений и систем нелинейных уравнений» по дисциплине «Информатика».
Цель и задачи работы:
1. Научиться создавать и применять ранжированные переменные.
2. Научиться строить графики в декартовой системе.
3. Научиться решению нелинейных уравнений и систем нелинейных уравнений с помощью решающего блока.
4. Решение системы линейных уравнений матричным способом.
При решении многих технических задач математические модели решения представляют собой нелинейные уравнения, системы нелинейных уравнений, системы линейных уравнений.
Уравнения и системы уравнений, возникающие в практических задачах, обычно можно решить только численно. Методы численного решения реализованы и в программе MathCad.
Для выполнения практической части:
Загрузить программу MathCAD с помощью ярлыка.
Сохранить файл в собственной папке под именем ….
Задание №1
Создать ранжированные переменные и вывести таблицы их значений
1. Создать ранжированную переменную z, которая имеет:
начальное значение 1
конечное значение 1.5
шаг изменения переменной 0.1
и вывести таблицу значений переменной z
2. Создать ранжированную переменную y, которая имеет:
начальное значение 2
конечное значение 7
шаг изменения переменной 1
и вывести таблицу значений переменной y
3. Создать ранжированную переменную t, которая имеет:
начальное значение a
конечное значение b
шаг изменения переменной h
и вывести таблицу значений переменной t
| Для создания ранжированных переменных используют Палитру
| Последовательность действий: 1. 2. (запятая) 3. ввести следующее значение (1.1) 4. нажимают кнопку 5. 1.5 (ввести конечное значение |
Если шаг изменения =1, то не выполняют пункты 2. и 3.
Для вывода таблицы значений, достаточно ввести имя переменной и знак ![]() .
.
Выполнение Задания №1
| 1.1 | 1.2 | 1.3 |
|
|
|
|
| Задание ранжированной переменной в виде | ||
Задание №2
Построить график функции
f(x)=sin(x)+ex-2 на диапазоне [-5; 2]
Выполнение задания №2
Последовательность действий:
1. Создать ранжированную переменную x

2. Создать функцию пользователя ![]()
| 3. Для построения графика использовать Палитру Graph и кнопку |
|
4. Ввести в место ввода по оси X имя независимого аргумента – x
5. Ввести в место ввода по оси Y – f(x)
6. Отвести от графика указатель мыши и щелкнуть левой кнопкой мыши. График будет построен

Рис. 1.1
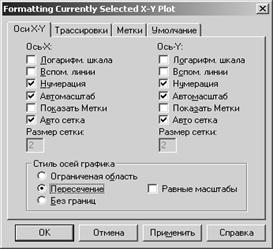
Для форматирования графика, дважды щелкнуть в области графика.
Появится диалоговое окно
| В этом окне 1.на Вкладке Ось X-Y установитьпереключатель Пересечение 2.на Вкладке Трассировки можно установить цвет и толщину линии |
Если щелкнуть по графику (появятся маркеры вокруг графика), то методом протягивания в нужном направлении можно изменить размеры графика.
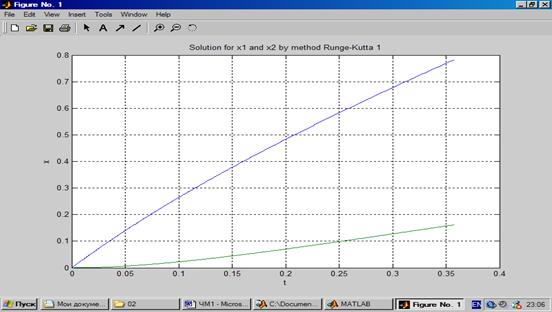
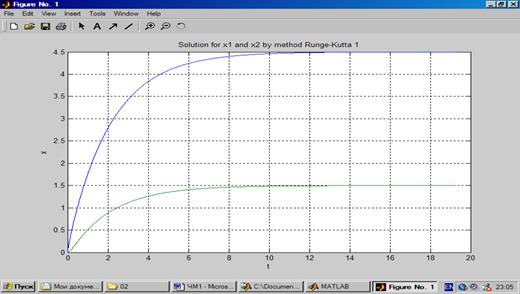
Так выглядит график после форматирования

Рис. 1.2
Теоретическая часть
Блок уравнений и неравенств, требующих решения, записывается после ключевого слова Given (дано). При записи уравнений используется знак логического равенства =, кнопка находится в Палитре Boolean.
Заканчивается блок решения вызовом функции Find (найти). В качестве аргументов этой функции – искомая величина. Если их несколько (при решении систем уравнений, то искомые неизвестные должны быть перечислены через запятую).
Всякое уравнение с одним неизвестным может быть записано в виде, f(x)=0,
где f(x) – нелинейная функция. Решение таких уравнений заключается в нахождении корней, т.е. тех значений неизвестного x, которые обращают уравнение в тождество. Точное решение нелинейного уравнения далеко не всегда возможно. На практике часто нет необходимости в точном решении уравнения. Достаточно найти корни уравнения с заданной степенью точности.
Процесс нахождения приближенных корней уравнения состоит из двух этапов:
1 этап. Отделение корней, т.е. разбиения области определения функции f(x), на отрезки, в каждом из которых содержится только один корень уравнения.
2 этап. Уточнение приближенных корней уравнения, т.е. доведение их до заданной степени точности.
Практическая часть
Задание №1
Постановка задачи:
Найти корень уравнения x3-x2=2 с точностью Е=0,00001
Приведем заданное уравнение к виду f(x)=0
x3-x2-2 =0 f(x)= x3-x2-2
Выполнение задания №1
Похожие работы
... , равным максимальному шагу способа с переменным шагом, одинаково · жесткость системы затрудняет анализ результата решения ЗАКЛЮЧЕНИЕ В данной работе был исследован явный метод Эйлера для решения обычных и жестких систем ОДУ. Было проанализировано влияние величины шага интегрирования на ошибку аппроксимации, и ее влиянии на число итераций. Для этого была написана программа (Приложение 1), ...
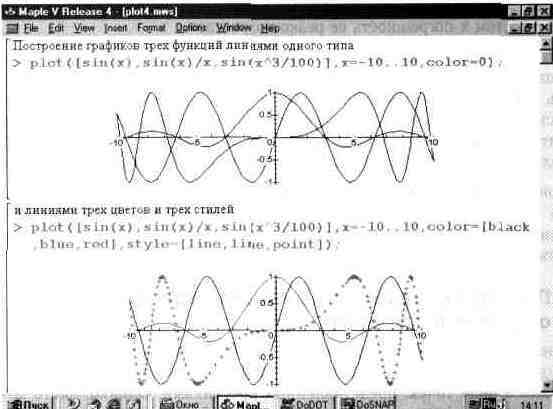
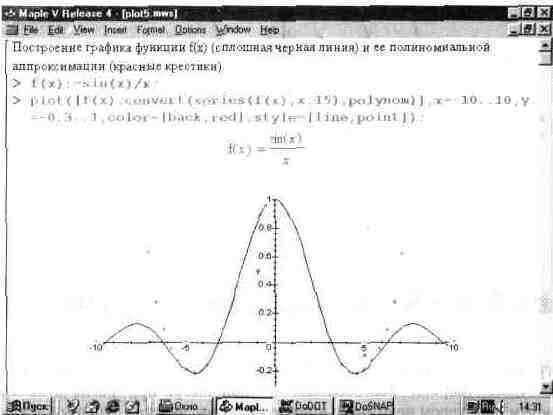
... типа MESH. 13.6. Графика пакета plots 13.6.1. Общая характеристика пакета plots Пакет plots содержит почти полсотни графических функции, существенно расширяющих возможности графики системы Maple V. В реализации R4 этот пакет содержит следующие функции: ——————————— animate Создает мультипликацию 2D графиков функций. animated Создает мультипликацию 3D графиков функции. changecoords ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
... , где Fi – функция n переменных. Решением СНАУ является вектор X=(X1,…,Xn), при подстановке компонент которого в систему каждое её уравнение обращается в верное равенство. При n=3 – точка пересечения трёх поверхностей. Модифицированный метод Ньютона – один из методов, применяющихся для нахождения корня СНАУ. Модифицированный метод Ньютона предполагает наличие начального приближения X0. Суть ...
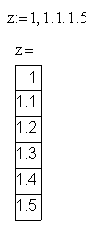
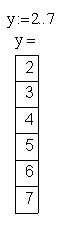





0 комментариев