Навигация
ПОВЕРХНЕВІ ІНТЕГРАЛИ
1. Поверхневі інтеграли першого роду
Поверхневі інтеграли першого роду є узагальненням подвійних інтегралів.
Нехай у точках деякої кусково-гладкої поверхні ![]() визначена обмежена функція
визначена обмежена функція ![]() . (Поверхня називається гладкою, якщо в кожній її точці існує дотична площина і при переході від точки до точки положення цієї дотичної площини змінюється неперервно. Поверхня, яка складається із скінченного числа неперервно з’єднаних гладких поверхонь, називається кусково-гладкою.) Розіб'ємо поверхню
. (Поверхня називається гладкою, якщо в кожній її точці існує дотична площина і при переході від точки до точки положення цієї дотичної площини змінюється неперервно. Поверхня, яка складається із скінченного числа неперервно з’єднаних гладких поверхонь, називається кусково-гладкою.) Розіб'ємо поверхню ![]() на
на ![]() довільних частин
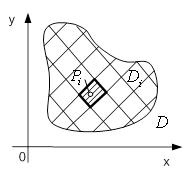
довільних частин ![]() без спільних внутрішніх точок (рис. 1); нехай
без спільних внутрішніх точок (рис. 1); нехай ![]() – площа, а
– площа, а ![]() – діаметр частини поверхні
– діаметр частини поверхні ![]() . У кожній частині
. У кожній частині ![]() виберемо довільну точку
виберемо довільну точку ![]() і складемо суму
і складемо суму
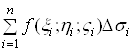 .(1)
.(1)
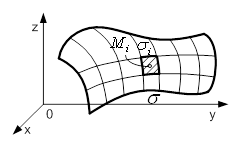
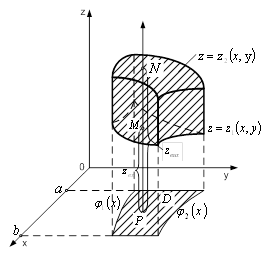
Рисунок 1 – Поверхня ![]()
Цю суму називають інтегральною сумою для функції ![]() по поверхні
по поверхні ![]() .
.
Якщо при ![]() інтегральні суми (1) мають скінченну межу, яка не залежить ні від способу розбиття поверхні
інтегральні суми (1) мають скінченну межу, яка не залежить ні від способу розбиття поверхні ![]() , ні від вибору точок
, ні від вибору точок ![]() , цю границю називають поверхневим інтегралом першого роду від функції
, цю границю називають поверхневим інтегралом першого роду від функції ![]() по поверхні
по поверхні ![]() і позначають
і позначають ![]() .
.
Таким чином, за означенням
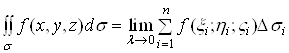 .(2)
.(2)
У цьому разі функція ![]() називається інтегровною по поверхні
називається інтегровною по поверхні ![]() , а поверхня
, а поверхня ![]() – областю інтегрування.
– областю інтегрування.
Якщо функція ![]() неперервна на поверхні
неперервна на поверхні ![]() , то вона інтегровна по
, то вона інтегровна по ![]() .
.
Обчислення поверхневого інтеграла першого роду зводиться до обчислення подвійного інтеграла.
Нехай гладка поверхня ![]() , задана рівнянням
, задана рівнянням ![]() , проектується на площину
, проектується на площину ![]() в область
в область ![]() . Припустимо, що функція
. Припустимо, що функція ![]() неперервна на поверхні
неперервна на поверхні ![]() , а функції
, а функції ![]() неперервні в області
неперервні в області ![]() .
.
Внаслідок розбиття поверхні ![]() на частини
на частини ![]() область
область ![]() розіб'ється на частини
розіб'ється на частини ![]() , які є відповідними проекціями частин
, які є відповідними проекціями частин ![]() на площину
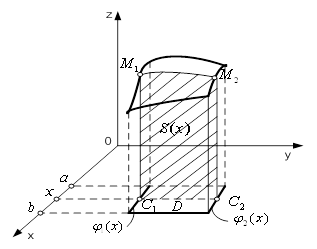
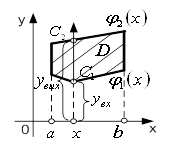
на площину ![]() (рис. 2).
(рис. 2).
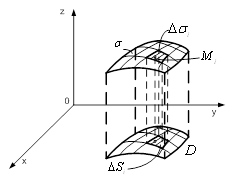
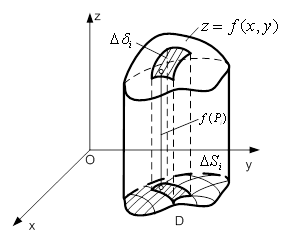
Рисунок 2 – Розбиття поверхні ![]() на частини
на частини ![]()
Якщо ![]() – площа області
– площа області ![]() ,
, ![]() – площа поверхні
– площа поверхні ![]() , то
, то
![]() ,
,
тому інтегральну суму (1) можна записати у вигляді
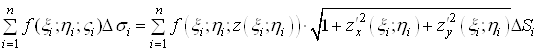 .(3)
.(3)
Права частина цієї рівності є інтегральною сумою для функції
![]() ,
,
тому з рівностей (2) і (3) випливає, що
![]() .(4)
.(4)
Формула (4) виражає поверхневий інтеграл першого роду через подвійний інтеграл по проекції поверхні ![]() на площину
на площину ![]() .
.
Аналогічно можна отримати формули, що виражають інтеграл по поверхні ![]() через подвійні інтеграли по її проекціях на площини
через подвійні інтеграли по її проекціях на площини ![]() та
та ![]() . Якщо поверхня
. Якщо поверхня ![]() задається рівнянням
задається рівнянням ![]() або
або ![]() , то
, то
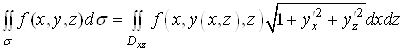
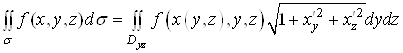 ,
,
де ![]() та
та ![]() – проекції поверхні
– проекції поверхні ![]() на координатні площини
на координатні площини ![]() та
та ![]() відповідно.
відповідно.
Якщо у формулі (2) покласти ![]() на поверхні
на поверхні ![]() , то отримаємо
, то отримаємо
![]() ,(5)
,(5)
де ![]() – площа поверхні
– площа поверхні ![]() , тобто за допомогою поверхневого інтеграла першого роду можна обчислювати площі поверхонь.
, тобто за допомогою поверхневого інтеграла першого роду можна обчислювати площі поверхонь.
Крім того, поверхневі інтеграли першого роду застосовують при обчисленні маси, координат центра маси, моменту інерції матеріальної поверхні з відомою поверхневою густиною розподілу маси. Виведення відповідних формул по суті не відрізняється від виводу аналогічних формул для матеріальної пластинки.
Якщо на кусково-гладкій поверхні ![]() розподілено масу з поверхневою густиною
розподілено масу з поверхневою густиною ![]() , то:
, то:
а) маса матеріальної поверхні
![]() ;
;
б) координати центра маси поверхні:
![]() ,
,
де ![]() – статичні моменти поверхні
– статичні моменти поверхні ![]() відносно осей
відносно осей ![]() ;
;
в) моменти інерції поверхні відносно осей координат і початку координат:
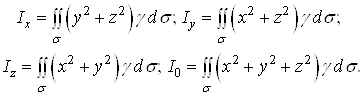
Похожие работы
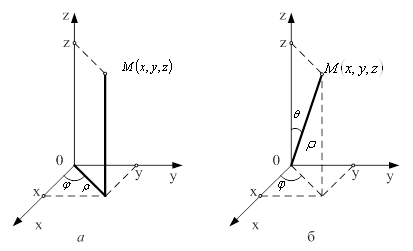
... прямокутних координат до сферичних (рис. 4, б), які пов'язані з формулами Рисунок 4 – Координати: а) циліндричні; б) сферичні ; , якобіан перетворення . З формули (8) знаходимо потрійний інтеграл у сферичних координатах: . (10) Назва «сферичні координати» пов'язана з тим, що координатна поверхня є сферою. При обчисленні потрійного інтеграла в циліндричних чи сферичних ...
... Під знаком границі маємо інтегральну суму, складену для неперервної в області функції . Ця функція інтегровна в області , тому границя у формулі (10) існує і дорівнює подвійному інтегралу (8). 3. Застосування подвійних інтегралів до задач механіки 1. Маса пластини. Нехай на площині маємо матеріальну пластину, яка має форму обмеженої замкненої області , в кожній точці якої густина визначає ...
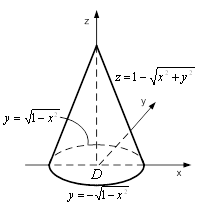
... йного інтеграла зводять до обчислення так званого повторного інтеграла - двох звичайних визначених інтегралів. Покажемо, як це робиться. Припустимо, що при функція . Тоді, згідно з формулою (7), подвійний інтеграл виражає об'єм циліндричного тіла (рис.3) з основою , обмеженого зверху поверхнею . Обчислимо цей об'єм за допомогою методу паралельних перерізів [6]: , де - площа перерізу тіла ...
... прийнятної точності необхідна велика кількість статистичних випробувань. Теорія методу Монте-Карло вивчає способи вибору випадкових величин для вирішення різних завдань, а також способи зменшення дисперсії випадкових величин. 3. Програма обчислення кратного інтеграла методом Монте-Карло Обчислити певний інтеграл . за методом “Монте-Карло” по формулі , де n – число випробувань ;g(x) – щі ...


0 комментариев