Навигация
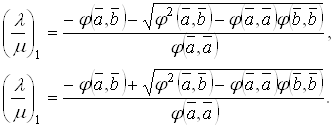
2.7 Модель Пуанкаре
Роль плоскости Лобачевского играет в модели Пуанкаре открытая полуплоскость; роль прямых выполняют содержащиеся в ней полуокружности с центрами на ограничивающей ее прямой и лучи, перпендикулярные этой прямой. Роль наложений выполняют композиции инверсий относительно этих полуокружностей и отражений лучах. Все аксиомы евклидовой геометрии здесь выполняются, кроме аксиомы параллельных, тем самым в этой модели выполняется геометрия Лобачевского.
Практическая часть
1. Сумма углов треугольника
Исследуем прежде всего связь постулатов Евклида и Лобачевского с вопросом о сумме углов треугольника. Покажем, что постулат Евклида равносилен предположению, что сумма углов треугольника равна двум прямым, а постулат Лобачевского - что сумма меньше двух прямых.
Прежде всего исключим предположение, что сумма углов треугольника может быть больше двух прямых.
Задача 1. Доказать, что сумма углов треугольника не может быть больше двух прямых.
Доказательство – от противного: предположим, что сумма углов треугольника АВС равна 2d. Пусть ВАС - наименьший угол этого треугольника (в частном случае, если АВС – равносторонний треугольник или равнобедренный треугольник, основание которого больше боковой стороны, то один из его равных углов). Проводим медиану AD противоположной стороны и откладываем отрезок DB1, равный этой медиане. из равенства треугольников ABD и B1DC выводим, что DB1C= DAB, DCB1= DBA. Таким образом, в треугольнике АВ1С (назовем его первым выводным треугольником) сумма трех углов равна также 2d, сумма двух углов с вершинами в конечных точках удвоенной медианы исходного треугольника равна, а наименьший угол. Из первого выводного треугольника получаем аналогичным построением второй выводной: берем наименьший угол, проводим медиану противолежащей стороны и т.д. В полученном таким образом втором выводном треугольнике сумма трех углов равна 2d, сумма двух углов с вершинами в конечных точках удвоенной медианы первого выводного треугольника, а наименьший угол. Продолжая этот процесс далее, получим ряд выводных треугольников; в n-м треугольнике сумма углов равна 2d, а сумма углов с вершинами в концах удвоенной медианы (n-1)-го выводного треугольника. Если взять n достаточно большим, то можно сделать меньше, т.е. третий угол этого треугольника будет больше 2d; мы получаем противоречие.
Задача 2. Доказать, что если в каком-нибудь треугольнике сумма углов равна 2d, то это имеет место и во всяком другом треугольнике
Доказательство. Обозначим сумму углов треугольника АВС через SАВС. Пусть в треугольнике АВС сумма углов равна 2d; тогда два угла, например А и С, острые, и нетрудно показать, что высота ВD, опущенная из вершины В, пройдет внутри этого треугольника, т.е. разобьет его на два прямоугольных треугольника. Учитывая, что
SABC=SABD+SDBC-2d, (1)
и принимая во внимание предыдущую теорему, выводим, что SABC=SABD=2d.
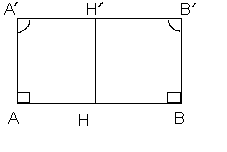
Покажем теперь, что в каждом прямоугольном треугольнике сумма углов равна 2d. Для этого возьмем треугольник ABD и дополним его до прямоугольника, пристроив к нему равный ему треугольник AEB с прямым углом в вершине Е и катетами АЕ=BD и EB=AD. В этом прямоугольнике AEBD сумма углов равна 4d. Откладывая сторону AD n раз прямой AY и прикладывая затем один к другому прямоугольники, равные AEBD, построим прямоугольник ALMK, составленный из n2 прямоугольников, равных AEBD. В прямоугольнике ALMK сумма углов равна 4d. Диагональ AM разбивает этот прямоугольник на два прямоугольных треугольника, в каждом из которых сумма углов равна 2d (на основании теоремы 1). Принимая n достаточно большим, получим прямоугольный треугольник AMK, у которого катеты будут больше некоторого заданного прямоугольного треугольника PQR. Откладывая отрезки QT=KM, QS=AK, получим прямоугольный треугольник STQ, равный прямоугольному треугольнику AMK и вмещающий в себе заданный прямоугольный треугольник PQR. Отрезок PT разбивает STQ на два треугольника, и так как SSQT=SSPT+SPTQ-2d, то SSPT+SPTQ=4d, откуда (на основании той же теоремы)
SSPT=SPTQ=2d.
Применяя то же рассуждение к треугольнику PTQ и отрезку RP, устанавливаем, что SPQR=2d.
Итак, в каждом прямоугольном треугольнике сумма углов равна 2d. Но мы видели выше, что каждый треугольник может быть разбит на два прямоугольных. Учитывая соотношение (1), получаем, что в любом треугольнике сумма углов равна 2d.
Итак, возможны только два предположения: или во всех треугольниках сумма углов равна 2d, или же во всех меньше 2d.
Теперь мы установим связь вопроса о сумме углов треугольника с постулатом параллельности.
Задача 3. Доказать, что если сумма углов треугольника равна 2d, то имеет место постулат Евклида, если же она меньше 2d, то справедлив постулат Лобачевского.
Имеет место и обратное предложение.
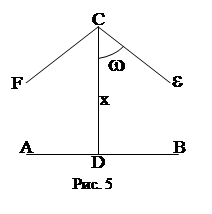
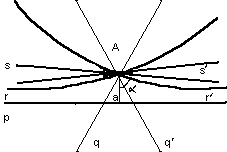
Доказательство. Прежде всего покажем, что если сумма углов треугольника равна 2d, то через точку Р, не лежащую на прямой АА1, можно провести прямую, образующую с прямой ВВ1(АА1 и ВВ1 перпендикулярны к PQ) сколь угодно малый угол и пересекающую АА1.
Для этого построим отрезок QQ1=PQ; тогда угол B1PQ1=d/2. Откладываем отрезок Q1Q2=PQ1; B1PQ=d/22. затем продолжаем этот процесс: смотрим отрезки Q2Q3=PQ2, Q3Q4=PQ3,......,Qn-1Qn=PQn-1. Получаем лучи PQ3, PQ4,......, PQn, образующие с лучом РВ1 углы d/23, d/24,......, d/2n. При увеличении n мы можем, таким образом, получить угол, меньше любого заданного.
Теперь уже просто доказать постулат Евклида. Пусть некоторый луч PR образует с PB1 угол. Выбирая n достаточно большими ( так, чтобы (d/2n)<), мы получим треугольник PQQn, причем луч РR проходит внутри угла QPQn, т.е. пересекает сторону QQn.
Рассмотрим теперь предположение, что сумма углов треугольника меньше 2d. Покажем, что имеются прямые, отличные от ВВ1, проходящие через точку Р и не пересекающие АА1.
Соединим некоторую точку М, лежащую на АА1, с Р и проведем луч PR так, чтобы МРR был равен РМQ. Из предположения о сумме углов треугольника вытекает, что МРВ1>РМQ, т.е. луч РR пройдет внутри угла МРВ1; этот луч не пересекает АА1, так как в противном случае получился треугольник, у которого внешний угол QMP равен внутреннему (МРR), с ним не смежному.
Таким образом, первая половина теоремы доказана, а из нее непосредственно вытекает обратное предложение.
Похожие работы
... 3. Б.Л. Лаптев. Н.И. Лобачевский и его геометрия. Пособие для учащихся. М. «Просвещение», 1970г. 4. И.М. Яглам. Принцип относительности Галилея и неевклидова геометрия.Серия «Библиотека математического кружка» М: 1963г. Приложение 1 Николай Иванович Лобачевский, второй сын мелкого чиновника, родился 1 декабря(20 ...
... , т. е. такие пары точек считаются за одну точку. Из этого определения следует, что при возрастании n число типов неевклидовых пространств также растет. Неевклидовы геометрии являются геометриями простейших римановых пространств определенной и неопределенной метрики, составляющих так называемый класс пространств постоянной ненулевой кривизны. Каждое из таких n-мерных пространств допускает ...
... метод координат. V. Аксіома паралельності Сама остання аксіома грає в геометрії особливу роль, визначаючи поділ геометрії на дві логічно несуперечливі й взаємно виключають один одного системи: Евклідову й неевклідову геометрії. У геометрії Евкліда ця аксіома формулюється так. V. Нехай а – довільна пряма й А – крапка, що лежить поза прямій а, тоді в площині α, обумовленою крапкою А и ...
... представить другие геометрии Кант счел достаточным основанием, чтобы утверждать, что другие геометрии не могут существовать. Появление неевклидовой геометрии Но многовековые попытки доказательства пятого постулата Евклида привели в конце концов к появлению новой геометрии, отличающейся от евклидовой тем, что в ней V постулат не выполняется. Эта геометрия теперь называется неевклидовой, а в ...
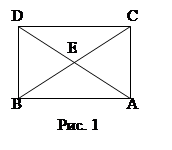

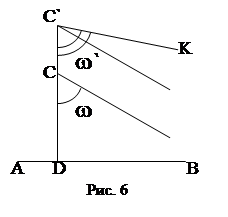
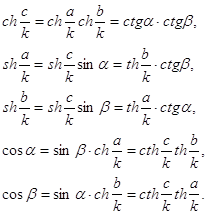
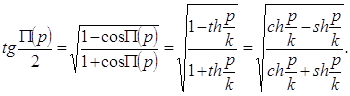
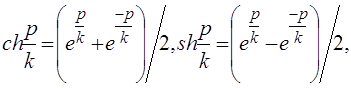
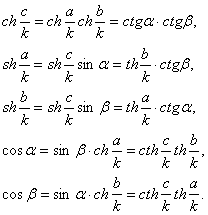
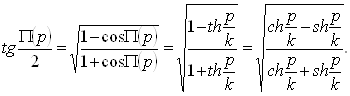
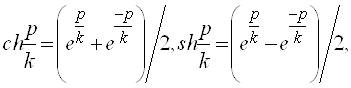
0 комментариев