Навигация
Любая цепь является дистрибутивной решёткой
2. Любая цепь является дистрибутивной решёткой.
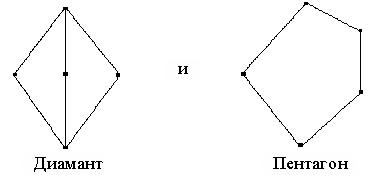 |
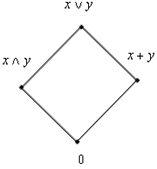
ТЕОРЕМА 1.2. Решётка L с 0 и 1 является дистрибутивной тогда и только тогда, когда она не содержит подрешёток вида
Доказательство этой теоремы можно найти в книге [1].
1.4. Обобщённо булевы решётки, булевы решётки
Всюду далее под словом «решётка» понимается произвольная дистрибутивная решётка с 0.
Решётка L называется обобщённой булевой, если для любых элементов ![]() и d из L, таких что
и d из L, таких что ![]() существует относительное дополнение на интервале
существует относительное дополнение на интервале ![]() , т.е. такой элемент
, т.е. такой элемент ![]() из L, что
из L, что ![]() и
и ![]() .
.
(Для ![]() ,
, ![]() , интервал
, интервал ![]() |
|![]() ; для
; для ![]() ,
, ![]() можно так же определить полуоткрытый интервал
можно так же определить полуоткрытый интервал ![]() |
|![]() ).
).
ТЕОРЕМА 1.3. (О единственности относительного дополнения в обобщённо булевой решётке). Каждый элемент обобщённо булевой решётки L имеет только одно относительное дополнение на промежутке.
Доказательство. Пусть для элемента ![]() существует два относительных дополнения
существует два относительных дополнения ![]() и
и ![]() на интервале
на интервале ![]() . Покажем, что
. Покажем, что ![]() . Так как
. Так как ![]() относительное дополнение элемента
относительное дополнение элемента ![]() на промежутке
на промежутке ![]() , то
, то ![]() и
и ![]() , так же
, так же ![]() относительное дополнение элемента
относительное дополнение элемента ![]() на промежутке
на промежутке ![]() , то
, то ![]() и
и ![]() .
.
Отсюда
![]()
![]() ,
,
таким образом ![]() , т.е. любой элемент обобщённой булевой решётки имеет на промежутке только одно относительное дополнение.
, т.е. любой элемент обобщённой булевой решётки имеет на промежутке только одно относительное дополнение.
Решётка L называется булевой, если для любого элемента ![]() из L существует дополнение, т.е. такой элемент
из L существует дополнение, т.е. такой элемент ![]() из L, что
из L, что ![]() и
и ![]()
ТЕОРЕМА 1.4. (О единственности дополнения в булевой решётке). Каждый элемент булевой решётки L имеет только одно дополнение.
Доказательство аналогично доказательству теоремы 1.3.
ТЕОРЕМА 1.5. (О связи обобщённо булевых и булевых решёток).
Любая булева решётка является обобщённо булевой, обратное утверждение не верно.
Доказательство. Действительно, рассмотрим произвольную булеву решётку L. Возьмём элементы a и d из L, такие что ![]() . Заметим, что относительным дополнением элемента a до элемента d является элемент
. Заметим, что относительным дополнением элемента a до элемента d является элемент ![]() , где a’ – дополнение элемента a в булевой решётке L. Действительно,
, где a’ – дополнение элемента a в булевой решётке L. Действительно, ![]() , кроме того
, кроме того ![]() . Отсюда следует, что решётка L является обобщённо булевой.
. Отсюда следует, что решётка L является обобщённо булевой.
1.5. Идеалы
Подрешётка I решётки L называется идеалом, если для любых элементов ![]() и
и ![]() элемент
элемент ![]() лежит в I. Идеал I называется собственным, если
лежит в I. Идеал I называется собственным, если ![]() . Собственный идеал решётки L называется простым, если из того, что
. Собственный идеал решётки L называется простым, если из того, что ![]() и
и ![]() следует
следует ![]() или
или ![]() .
.
Так как непустое пересечение любого числа идеалов снова будет идеалом, то мы можем определить идеал, порождённый множеством H в решётке L, предполагая, что H не совпадает с пустым множеством. Идеал, порождённый множеством H будет обозначаться через (H]. Если ![]() , то вместо
, то вместо ![]() будем писать
будем писать ![]() и называть
и называть ![]() главным идеалом.
главным идеалом.
ТЕОРЕМА 1.5. Пусть L – решётка, а H и I – непустые подмножества в L, тогда I является идеалом тогда и только тогда, когда если ![]() , то
, то ![]() , и если
, и если ![]() , то
, то ![]() .
.
Доказательство. Пусть I – идеал, тогда ![]() влечёт за собой
влечёт за собой ![]() , так как I – подрешётка. Если
, так как I – подрешётка. Если ![]() , то
, то ![]() и условия теоремы проверены.
и условия теоремы проверены.
Обратно, пусть I удовлетворяет этим условиям и ![]() . Тогда
. Тогда ![]() и так как
и так как ![]() , то
, то ![]() , следовательно, I – подрешётка. Наконец, если
, следовательно, I – подрешётка. Наконец, если ![]() и
и ![]() , то
, то ![]() , значит,
, значит, ![]() и I является идеалом.
и I является идеалом.
Глава 2 2.1. Конгруэнции
Отношение эквивалентности (т.е. рефлексивное, симметричное и транзитивное бинарное отношение) ![]() на решётке L называется конгруэнцией на L, если
на решётке L называется конгруэнцией на L, если ![]() и
и ![]() совместно влекут за собой
совместно влекут за собой ![]() и
и ![]() (свойство стабильности). Простейшими примерами являются ω, ι, определённые так:
(свойство стабильности). Простейшими примерами являются ω, ι, определённые так:
![]() (ω)
(ω)![]()
![]() ;
; ![]() (ι) для всех
(ι) для всех ![]() .
.
Для ![]() обозначим через
обозначим через ![]() смежный класс, содержащий элемент
смежный класс, содержащий элемент ![]() , т.е.
, т.е. ![]() |
|![]()
Пусть L – произвольная решётка и ![]() . Наименьшую конгруэнцию, такую, что
. Наименьшую конгруэнцию, такую, что ![]() для всех
для всех ![]() , обозначим через
, обозначим через ![]() и назовём конгруэнцией, порождённой множеством
и назовём конгруэнцией, порождённой множеством ![]() .
.
ЛЕММА 2.1. Конгруэнция ![]() существует для любого
существует для любого ![]() .
.
Доказательство. Действительно, пусть Ф = ![]() |
|![]() для всех
для всех ![]()
![]() . Так как пересечение в решётке
. Так как пересечение в решётке ![]() совпадает с теоретико-множественным пересечением, то
совпадает с теоретико-множественным пересечением, то ![]() для всех
для всех ![]() . Следовательно, Ф=
. Следовательно, Ф=![]() .
.
В двух случаях мы будем использовать специальные обозначения: если ![]() или
или ![]() и
и ![]() - идеал, то вместо
- идеал, то вместо ![]() мы пишем
мы пишем ![]() или
или ![]() соответственно. Конгруэнция вида
соответственно. Конгруэнция вида ![]() называется главной; её значение объясняется следующей леммой:
называется главной; её значение объясняется следующей леммой:
ЛЕММА 2.2. ![]() =
=![]() |
|![]() .
.
Доказательство. Пусть ![]() , тогда
, тогда ![]() , отсюда
, отсюда ![]() . С другой стороны рассмотрим
. С другой стороны рассмотрим ![]() , но тогда
, но тогда ![]() . Поэтому
. Поэтому ![]() и
и ![]() .
.
Заметим, что ![]() - наименьшая конгруэнция, относительно которой
- наименьшая конгруэнция, относительно которой ![]() , тогда как
, тогда как ![]() - наименьшая конгруэнция, такая, что
- наименьшая конгруэнция, такая, что![]() содержится в одном смежном классе. Для произвольных решёток о конгруэнции
содержится в одном смежном классе. Для произвольных решёток о конгруэнции ![]() почти ничего не известно. Для дистрибутивных решёток важным является следующее описание конгруэнции
почти ничего не известно. Для дистрибутивных решёток важным является следующее описание конгруэнции ![]() :
:
ТЕОРЕМА 2.1. Пусть ![]() - дистрибутивная решётка,
- дистрибутивная решётка, ![]() и
и ![]() . Тогда
. Тогда ![]() и
и ![]() .
.
Доказательство. Обозначим через Ф бинарное отношение, определённое следующим образом: ![]() и
и ![]() .
.
Покажем, что Ф – отношение эквивалентности:
1) Ф – отношение рефлексивности: x·a = x·a ; x+b = x+b;
2) Ф – отношение симметричности:
![]()
![]() x·a = y·a и x+b = y+b
x·a = y·a и x+b = y+b ![]() y·a = x·a и y+b = x+b
y·a = x·a и y+b = x+b ![]()
![]() ;
;
3) Ф – отношение транзитивности.
Пусть ![]()
![]() x·a = y·a и x+b = y+b и пусть
x·a = y·a и x+b = y+b и пусть ![]()
![]() y·с = z·с и y+d = z+d. Умножим обе части x·a = y·a на элемент с, получим x·a·c = y·a·c. А обе части y·с = z·с умножим на элемент a, получим y·c·a = z·c·a. В силу симметричности x·a·c = y·a·c = z·a·c. Аналогично получаем x+b+d = y+b+d = z+b+d. Таким образом
y·с = z·с и y+d = z+d. Умножим обе части x·a = y·a на элемент с, получим x·a·c = y·a·c. А обе части y·с = z·с умножим на элемент a, получим y·c·a = z·c·a. В силу симметричности x·a·c = y·a·c = z·a·c. Аналогично получаем x+b+d = y+b+d = z+b+d. Таким образом ![]() .
.
Из всего выше обозначенного следует, что Ф – отношение эквивалентности.
Покажем, что Ф сохраняет операции. Если ![]() и z
и z![]() L, то (x+z) ·a = (x·a) + (z·a) = (y·a) + (z·a) = (y+z) ·a и (x+z)+b = z+(x+b) = z+(y+b); следовательно,
L, то (x+z) ·a = (x·a) + (z·a) = (y·a) + (z·a) = (y+z) ·a и (x+z)+b = z+(x+b) = z+(y+b); следовательно, ![]() . Аналогично доказывается, что
. Аналогично доказывается, что ![]() и, таким образом, Ф – конгруэнция.
и, таким образом, Ф – конгруэнция.
Наконец, пусть ![]() - произвольная конгруэнция, такая, что
- произвольная конгруэнция, такая, что ![]() , и пусть
, и пусть ![]() . Тогда x·a = y·a, x+b = y+b ,
. Тогда x·a = y·a, x+b = y+b , ![]() и
и ![]() . Поэтому вычисляя по модулю
. Поэтому вычисляя по модулю ![]() , получим
, получим
![]()
![]()
![]() , т.е.
, т.е. ![]() , и таким образом,
, и таким образом, ![]() .
.
СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ 2.1. Пусть I – произвольный идеал дистрибутивной решётки L. Тогда ![]() в том и только том случае, когда
в том и только том случае, когда ![]() для некоторого
для некоторого ![]() . В частности, идеал I является смежным классом по модулю
. В частности, идеал I является смежным классом по модулю ![]() .
.
Доказательство. Если ![]() , то
, то ![]() и элементы x·y·i, i принадлежат идеалу I.
и элементы x·y·i, i принадлежат идеалу I.
Действительно ![]() .
.
Покажем, что ![]() .
.
Воспользуемся тем, что ![]() (*), заметим, что
(*), заметим, что ![]() и
и ![]() , поэтому мы можем прибавить к тождеству (*)
, поэтому мы можем прибавить к тождеству (*) ![]() или
или ![]() , и тождество при этом будет выполняться.
, и тождество при этом будет выполняться.
![]() Прибавим
Прибавим ![]() :
: ![]() , получим
, получим ![]() .
.
![]() Прибавим
Прибавим ![]() :
: ![]() , получим
, получим ![]() .
.
Отсюда ![]() . Таким образом,
. Таким образом,![]() .
.
Обратно согласно лемме 2, ![]() |
|![]()
Однако ![]() и поэтому
и поэтому ![]() |
|![]()
Если ![]() , то
, то ![]() откуда
откуда
![]() .
.
Действительно, ![]() (**).
(**).
Рассмотрим правую часть этого тождества:
Объединим первое и второе слагаемые –
![]() .
.
Объединим первое и третье слагаемые –
![]() ,
,
таким образом ![]() (***)
(***)
Заметим, что ![]() , поэтому прибавим к обеим частям выражения (***) y:
, поэтому прибавим к обеим частям выражения (***) y:
![]()
![]()
Но ![]() , отсюда
, отсюда ![]() .
.
Следовательно, условие следствия из теоремы 2.1. выполнено для элемента ![]() . Наконец, если
. Наконец, если ![]() и
и ![]() , то
, то ![]() , откуда
, откуда ![]() и
и ![]() , т.е.
, т.е. ![]() является смежным классом.
является смежным классом.
ТЕОРЕМА 2.2. Пусть L – булева решётка. Тогда отображение ![]()
![]()
![]() является взаимно однозначным соответствием между конгруэнциями и идеалами решётки L. (Под
является взаимно однозначным соответствием между конгруэнциями и идеалами решётки L. (Под ![]()
![]() понимаем класс нуля по конгруэнции
понимаем класс нуля по конгруэнции ![]() , под
, под ![]() понимаем решётку конгруэнций.)
понимаем решётку конгруэнций.)
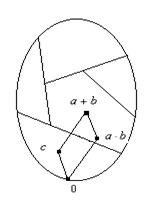 Доказательство. В силу следствия из теоремы 2.1. это отображение на множество идеалов; таким образом мы должны только доказать, что оно взаимно однозначно, т.е. что смежный класс
Доказательство. В силу следствия из теоремы 2.1. это отображение на множество идеалов; таким образом мы должны только доказать, что оно взаимно однозначно, т.е. что смежный класс ![]() определяет конгруэнцию
определяет конгруэнцию ![]() . Это утверждение, однако, очевидно. Действительно
. Это утверждение, однако, очевидно. Действительно ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() (*), последнее сравнение в свою очередь равносильно сравнению
(*), последнее сравнение в свою очередь равносильно сравнению ![]() , где с – относительное дополнение элемента
, где с – относительное дополнение элемента ![]() в интервале
в интервале ![]() .
.
Действительно, помножим выражение (*) на с:
![]() , но
, но![]() , а
, а ![]() , отсюда
, отсюда ![]() .
.
Таким образом, ![]() в том и только том случае, когда
в том и только том случае, когда ![]() .
.
Примечание. Приведённое доказательство не полностью использует условие, что L – дистрибутивная решётка с дополнениями. Фактически, мы пользовались только тем, что L имеет нуль и является решёткой с относительными дополнениями. Такая решётка называется обобщённой булевой решёткой.
ТЕОРЕМА 2.3 (Хасимото [1952]). Пусть L – произвольная решётка. Для того, чтобы существовало взаимно однозначное соответствие между идеалами и конгруэнциями решётки L, при котором идеал, соответствующий конгруэнции ![]() , являлся бы смежным классом по
, являлся бы смежным классом по ![]() , необходимо и достаточно, чтобы решётка L была обобщённой булевой.
, необходимо и достаточно, чтобы решётка L была обобщённой булевой.
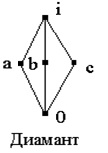 Доказательство. Достаточность следует из доказательства теоремы 2.2. Перейдём к доказательству необходимости.
Доказательство. Достаточность следует из доказательства теоремы 2.2. Перейдём к доказательству необходимости.
Идеалом, соответствующим конгруэнции ![]() , должен быть (0]; следовательно, L имеет нуль 0.
, должен быть (0]; следовательно, L имеет нуль 0.
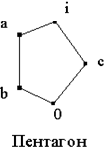 Если L содержит диамант
Если L содержит диамант ![]() , то идеал (a] не может быть смежным классом, потому что из
, то идеал (a] не может быть смежным классом, потому что из ![]() следует
следует ![]() и
и ![]() . Но
. Но ![]() , значит, любой смежный класс, содержащий
, значит, любой смежный класс, содержащий ![]() , содержит и
, содержит и ![]() , и
, и ![]() .
.
Аналогично, если L содержит пентагон ![]() и смежный класс содержит идеал
и смежный класс содержит идеал ![]() , то
, то ![]() и
и ![]() , откуда
, откуда ![]() . Следовательно, этот смежный класс должен содержать
. Следовательно, этот смежный класс должен содержать ![]() и
и ![]() .
.
Итак, решётка L не содержит подрешёток, изоморфных ни диаманту, ни пентагону. Поэтому, по теореме 1.2., она дистрибутивна.
Пусть ![]() и
и ![]() . Согласно следствию из теоремы 2.1., для конгруэнции
. Согласно следствию из теоремы 2.1., для конгруэнции ![]() идеал
идеал ![]() так же является смежным классом, следовательно,
так же является смежным классом, следовательно, ![]() , откуда
, откуда ![]() . Опять применяя следствие из теоремы 2.1. получим,
. Опять применяя следствие из теоремы 2.1. получим, ![]() для некоторого
для некоторого ![]() . Так как
. Так как ![]() , то
, то ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() о полу орого ледствие 4 получим, цииодержать , соответствующим конгруэнции
образом мы должны только доказать, ______________ и
о полу орого ледствие 4 получим, цииодержать , соответствующим конгруэнции
образом мы должны только доказать, ______________ и ![]() , т.е. элемент
, т.е. элемент ![]() является относительным дополнением элемента
является относительным дополнением элемента ![]() в интервале
в интервале ![]() .
.
2.2. Основная теорема
(1)  Пусть
Пусть ![]() - обобщённая булева решётка. Определим бинарные операции
- обобщённая булева решётка. Определим бинарные операции ![]() на B, полагая
на B, полагая ![]() и обозначая через
и обозначая через ![]() относительное дополнение элемента
относительное дополнение элемента ![]() в интервале
в интервале ![]() . Тогда
. Тогда ![]() - булево кольцо, т.е. (ассоциативное) кольцо, удовлетворяющее тождеству
- булево кольцо, т.е. (ассоциативное) кольцо, удовлетворяющее тождеству ![]() (а следовательно и тождествам
(а следовательно и тождествам ![]() ,
, ![]() ).
).
(2) Пусть ![]() - булево кольцо. Определим бинарные операции
- булево кольцо. Определим бинарные операции ![]() и
и ![]() на
на ![]() , полагая, что
, полагая, что ![]() и
и ![]() . Тогда
. Тогда ![]() - обобщённая булева решётка.
- обобщённая булева решётка.
Доказательство.
(1) Покажем, что ![]() - кольцо.
- кольцо.
Напомним определение. Кольцо ![]() - это непустое множество
- это непустое множество ![]() с заданными на нём двумя бинарными операциями
с заданными на нём двумя бинарными операциями ![]() , которые удовлетворяют следующим аксиомам:
, которые удовлетворяют следующим аксиомам:
1. Коммутативность сложения: ![]() выполняется
выполняется ![]() ;
;
2. Ассоциативность сложения: ![]() выполняется
выполняется ![]() ;
;
3. Существование нуля, т.е. ![]() ,
, ![]() ;
;
4. Существование противоположного элемента, т.е. ![]() ,
, ![]() ,
, ![]() ;
;
5. Ассоциативность умножения: ![]() ,
, ![]() ;
;
0 комментариев