Навигация
1.2 Лема про рукостискання
Формулювання цієї леми просте – „кількість рук, що приймають участь у рукостисканні N-пар людей, дорівнює 2*N”. Лему можна представити у формі графу, де N вершин з’єднані ребрами d(xi,xj) рукостискання i та j – вершин (див. рис.1.12), виконавши наступне доведення.
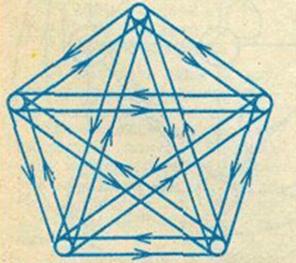
Рис.1.12. „Лема про рукостискання” 5 осіб у вигляді графу „взаємно-простягнутих рук” (10 пар рук для повної множини рукостискань) [3]
Нехай ![]() граф з множиною верщин
граф з множиною верщин ![]() . Тоді
. Тоді
![]() (1.1)
(1.1)
Доведення. Зауважимо,що кожне ребро графа в сумі ![]() враховується двічі (див. рис.1.5), і тому спараведива рівність (1.1). Зауважимо, що сума сту-пенів усіх вершин у графі (або мультіграфі без петель) повинна бути парною. Це випливає з того, що якщо взяти вершини, взагалі не пов'язані одна з одною, то сума ступенів цих вершин дорівнює нулю. Додаючи будь-яке ребро, що пов'язує дві вершини, збільшуємо суму всіх ступенів на 2 одиниці. Таким чи-ном, сума всіх ступенів вершин парна. З рівності 1.1 випливає такє твердження: число вершин непарного степеня в графі
враховується двічі (див. рис.1.5), і тому спараведива рівність (1.1). Зауважимо, що сума сту-пенів усіх вершин у графі (або мультіграфі без петель) повинна бути парною. Це випливає з того, що якщо взяти вершини, взагалі не пов'язані одна з одною, то сума ступенів цих вершин дорівнює нулю. Додаючи будь-яке ребро, що пов'язує дві вершини, збільшуємо суму всіх ступенів на 2 одиниці. Таким чи-ном, сума всіх ступенів вершин парна. З рівності 1.1 випливає такє твердження: число вершин непарного степеня в графі ![]() обовязково є парним числом.
обовязково є парним числом.
Для визначення матриці суміжності, розглянемо граф ![]() . Нехай
. Нехай
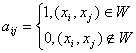
Означення 1.7.
Матриця ![]() називається матрицею суміжності ( інцидентності) графа
називається матрицею суміжності ( інцидентності) графа ![]() .
.
Матриця суміжності ![]() - це симетрична матриця, елементи якої до-рівнюють нулеві або одиниці ( діагональні елементи дорівнюють нулеві) і така, що сума чисел в будь-якому рядку і будь-якому стовпці дорівнює степені від-повідної вершини. Так, для графу, наведеного на рис.1.13, матриця суміжності побудується у вигляді:
- це симетрична матриця, елементи якої до-рівнюють нулеві або одиниці ( діагональні елементи дорівнюють нулеві) і така, що сума чисел в будь-якому рядку і будь-якому стовпці дорівнює степені від-повідної вершини. Так, для графу, наведеного на рис.1.13, матриця суміжності побудується у вигляді:
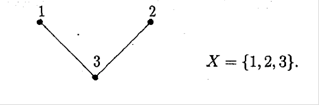
Рис.1.13. До побудови матриці суміжності 3-х вершинного графу
Означення 1.8.
Послідовність ребер![]()
![]() , в якій сусідні ребра інцидентні одній і тій же вершині називаються ланцюгом. Ланцюг називається простим, якщо всі вершини, належні йому (крім, можливо, першої і останньої), різні; число в цьому випадку називають довжиною ланцюга.
, в якій сусідні ребра інцидентні одній і тій же вершині називаються ланцюгом. Ланцюг називається простим, якщо всі вершини, належні йому (крім, можливо, першої і останньої), різні; число в цьому випадку називають довжиною ланцюга.
Якщо ![]() , то ланцюг називається циклом. Цикл, в якому всі вершини різні, називається простим. Приклади простих ланцюгів та простих циклів наведені на рис.1.14:
, то ланцюг називається циклом. Цикл, в якому всі вершини різні, називається простим. Приклади простих ланцюгів та простих циклів наведені на рис.1.14:
(1,3), (3,4), (4,6) – простий ланцюг;
(1,2), (2,5), (5,6) – простий ланцюг;
(1,3), (3,4), (4,6), (6,5), (5,2)Ю (2,1) – простий цикл.
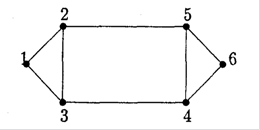
Рис 1.14. Приклад графа з простими ланцюгами та простими циклами
Означення 1.9.
Граф ![]() є підграфом графа
є підграфом графа ![]() , якщо
, якщо ![]() .Якщо
.Якщо ![]() , то підграф
, то підграф ![]() називається остовним підграфом.
називається остовним підграфом.
Означення 1.10.
Граф ![]() є сумою графів
є сумою графів ![]() , якщо
, якщо
![]()
ця сума називається прямою, якщо ![]() ,
, ![]()
1.3 Оцінки для числа ребер з ![]() компонентами зв ‘язності
компонентами зв ‘язності
Означення 1.11.
Граф ![]() називається зв язним , якщо будь-які вершини
називається зв язним , якщо будь-які вершини ![]() та
та ![]()
![]() сполучені ланцюгом з початком в
сполучені ланцюгом з початком в ![]() і кінцем в
і кінцем в ![]() . З симетрії випливає, що в цьому випадку і вершина
. З симетрії випливає, що в цьому випадку і вершина ![]() сполучена з вершиною
сполучена з вершиною ![]() .
.
Теорема 1.2.
Кожен граф є прямою сумою зв язних графів.
Доведення. На множині вершин ![]() граф
граф ![]() визначимо відношення
визначимо відношення
![]() , якщо
, якщо ![]() сполучається з
сполучається з ![]() .Відношення
.Відношення ![]() є відношенням еквівалентнос-ті. Позначимо через
є відношенням еквівалентнос-ті. Позначимо через ![]() .Тоді
.Тоді ![]() і є розбиття
і є розбиття ![]() на класи еквівалентності. Графи
на класи еквівалентності. Графи ![]() є зв язними графами і
є зв язними графами і
![]() (1.2)
(1.2)
є прямою сумою зв’язних графів.
Ці графи називаються компонентами зв’язності.
Розглянемо оцінки для числа ребер з ![]() компонентами зв’язності.
компонентами зв’язності.
Теорема 1.3.
Нехай ![]() граф, який складається з
граф, який складається з ![]() вершин,
вершин, ![]() ребер і
ребер і ![]() компонент зв язності. Тоді виконуються нерівності
компонент зв язності. Тоді виконуються нерівності
![]()
Доведення . Доведемо спочатку нерівність ![]() .Будемо доводити індукцією за числом ребер. Припустимо, що нерівність справедлива для всіх графів з числом ребер
.Будемо доводити індукцією за числом ребер. Припустимо, що нерівність справедлива для всіх графів з числом ребер ![]() . Нехай
. Нехай ![]() граф з
граф з ![]() вершин,
вершин, ![]() ребер і
ребер і ![]()
компонентами зв’язності. Викреслимо максимальне можливе число ребер так, щоб не змінювалося число компонент зв’язностя. Число ребер в отриманому графі позначемо ![]() .
.
Розглянемо для прикладу граф, зображений на рисунку (1.15)
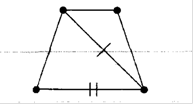
Рис. 1.15. Приклад 1 графу для оцінки зв’язності
В ньому ![]() .Викресливши два ребра, отримаємо граф
.Викресливши два ребра, отримаємо граф ![]() . Викреслити далі яке-небудь ребро, не порушуючи зв язності, вже не можна (див.рис.1.16).
. Викреслити далі яке-небудь ребро, не порушуючи зв язності, вже не можна (див.рис.1.16).
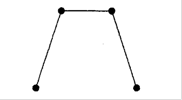
Рис. 1.16. Приклад 1 графу для оцінки зв’язності
Повернемося до графу, отриманого з ![]() . Викресливши в ньому ще одне ребро, ми отримаємо граф з числом компонент зв язності на одиницю більшим. В силу індуктивного припущення, справедливого, бо
. Викресливши в ньому ще одне ребро, ми отримаємо граф з числом компонент зв язності на одиницю більшим. В силу індуктивного припущення, справедливого, бо ![]() , маємо
, маємо ![]() , звідки
, звідки ![]() .
.
Для доведення верхньої оцінки в нерівності (1.3) замінимо кожну компо-ненту повним графом. Нехай ![]() та
та ![]() два повних, отриманих з компонент зв’ язності
два повних, отриманих з компонент зв’ язності ![]() та
та ![]() , а
, а ![]() та
та ![]() число ребер в цих компонентах
число ребер в цих компонентах ![]() . Замінемо
. Замінемо ![]() на повний граф, додавши одну вершину, а
на повний граф, додавши одну вершину, а ![]() замінемо на повний граф, віднявши одну вершину. Тоді загальне число вершин не змінеться, а число ребер збільшиться на додатню величину
замінемо на повний граф, віднявши одну вершину. Тоді загальне число вершин не змінеться, а число ребер збільшиться на додатню величину
![]()
Отже, для того, щоб число ребер у графі ![]() було максимально можливим (при фіксованих
було максимально можливим (при фіксованих ![]() і
і ![]() ), граф
), граф ![]() повинен складатись з
повинен складатись з ![]() ізольованих вершин і повного графа з
ізольованих вершин і повного графа з ![]() вершинами.Звідси й випливає нерівність (1.3). Теорема доведена.
вершинами.Звідси й випливає нерівність (1.3). Теорема доведена.
З нерівності (1.3) випливає такий наслідок.
Наслідок. Будь-який граф з ![]() і більше ніж
і більше ніж ![]() ребрами є зв’язним.
ребрами є зв’язним.
Справді, якщо граф з ![]() вершинами має дві компоненти зв’язності, то максимальне число ребер не перевищує
вершинами має дві компоненти зв’язності, то максимальне число ребер не перевищує ![]() .
.
Найти компоненти сильної зв’язності графу на рис.1.17.
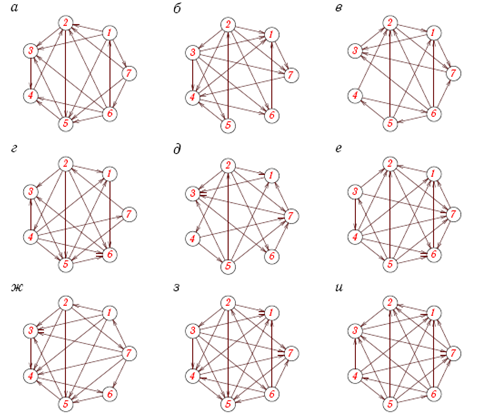
Відповіді
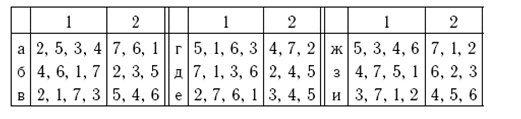
Рис.1.17. 7-ми вершинний граф для обчислення компонентів зв’язності [10]
0 комментариев