Навигация
Интеграл по поверхности первого рода
Содержание
1) Интеграл по поверхности первого рода
2) Специальные векторные поля
3) Теорема Стокса
4) Потенциальное поле
Литература
векторное потенциальное поле интеграл
Интеграл по поверхности первого рода
Физические задачи приводящие к поверхностному интегралу могут быть двух типов:
1) ![]() не связана с направлением нормали к поверхности
не связана с направлением нормали к поверхности
Например, задачи об отыскании массы или заряда распределенных по поверхности: ![]()
2) ![]() - зависит от направления нормали
- зависит от направления нормали ![]() -задача об отыскании потока жидкости в направлении нормали.
-задача об отыскании потока жидкости в направлении нормали.
Дано: ![]() -непрерывная функция на
-непрерывная функция на ![]()
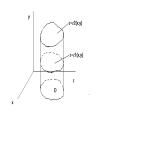
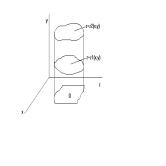
![]() -поверхность:
-поверхность: ![]()
![]()
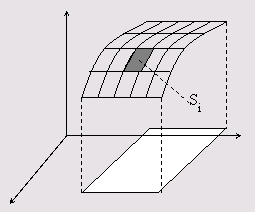
1) Разобьем поверхность на n частей ![]()
2) Возьмем точку ![]()
![]()
3) Вычислим ![]() -плотность
-плотность
4) ![]() -масса
-масса
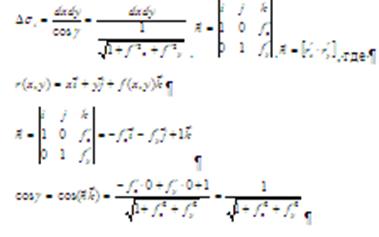
![]()
Следовательно
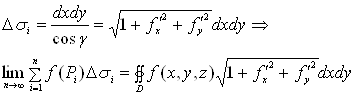
![]() ,
,
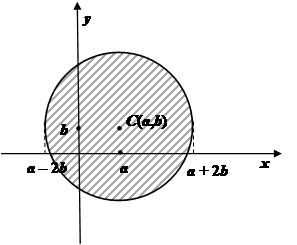
где D- проекция ![]() на плоскость XOY
на плоскость XOY
Пример.
![]() ,
,![]()

Пример. Определить массу, распределенную на поверхности ![]() , плотностью
, плотностью ![]()
Решение.
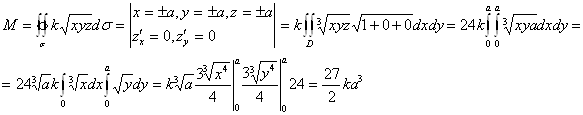
Специальные векторные поля.
1 Дивергенция.
2 Соленоидальные поля. Свойства.
3 ![]()
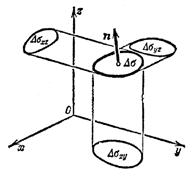
1. Определение дивергенции
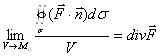
Теорема Остроградского -Гаусса
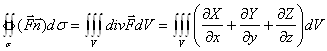
Пример. ![]()
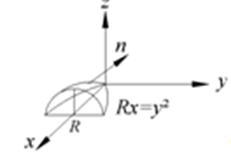
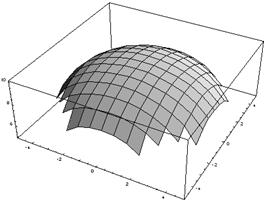
Найти поток вектора ![]() направленный в отрицательную сторону оси Ох, через часть параболоида
направленный в отрицательную сторону оси Ох, через часть параболоида ![]() отсекаемый плоскостью
отсекаемый плоскостью ![]()
Решение:
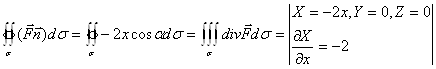
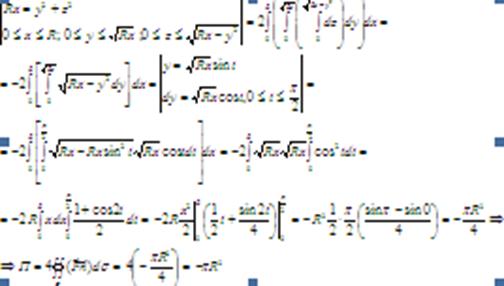
Ответ.![]()
Свойства соленоидальных полей.
Определение. Векторное поле , для всех точек которого ![]() называется соленоидальным в области
называется соленоидальным в области ![]() . Соленоидальное поле свободно от источников.
. Соленоидальное поле свободно от источников.
Свойства соленоидальных полей.
Похожие работы
... ; U’V+UV’+UV*P(x)=Q(x) ; U’V+U(V’+V*P(x))=Q(x) Найдём V ,чтобы V’+VP(x)=0 : Тогда U’V=Q(x) y’+y cos(x)=1/2 sin(2x) y=UV U’V+UV’+UVcos(x)=sin(x)cos(x) V’+Vcos(x)=0 dV/V=-cos(x)dx ln(V)= -sin(x) V=e-sin(x) sin(x)=t Билет №22 Уравнение Бернулли и Рикотти и их решение. Уравнение Бернулли – это диф. Ур-е следующего вида : где P(x) и Q(x) – непрерывные функции m – ...
ормулу Грина для области Д: D P(x,y), Q(x,y) , Вычисление площадей через крив интеграл Применим ф. Грина, т.е. выразим его через криволинейный интеграл по границе области. 1. Q = x P = 0 2. Q = 0 P = -y Суммируем 1 и 2 : Пример: Вычислить площадь эллипса . Сделаем замену переменных 0 £ t £ 2p Вопрос №6 Неприрывную кривую назыв. простой кривой ( ...
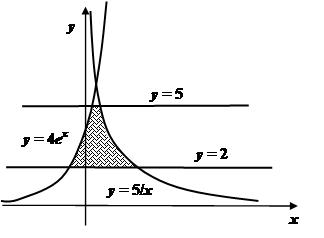
... так: , (10) где F1 и F2 – функции, полученные при подстановке в функцию f вместо x, y, z их выражений через цилиндрические (8) или сферические (9) координаты. 1.4 Геометрические и физические приложения кратных интегралов 1) Площадь плоской области S: (11) Пример 1. Найти площадь фигуры D, ограниченной линиями у = 2, у = 5. Решение. Эту площадь удобно вычислять, считая у ...
... с вершинами в точках А(0;0), В(0;1), С(½; 0). Найдем координаты единичной нормали к плоскости: Вычислим соответствующий поверхностный интеграл: Заключение В данной работе была рассмотрена дискретная теория поля. Вначале было введено понятие поверхностного интеграла. Поверхностный интеграл первого рода от функции f(M) = f(x, y, z) по поверхности S обозначается . ...
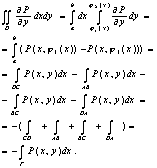
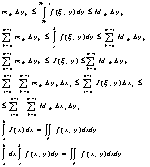


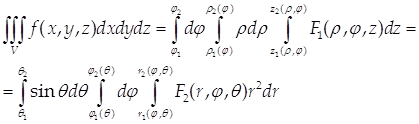


0 комментариев