Навигация
3 Описание тестовых задач
В данной работе спроектированы программа, реализующие методы простой итерации и Ньютона применительно к решению систем нелинейных уравнений. Для проверки предлагается решение системы уравнений с последующим исследованием рассматриваемых методов на её примере. При этом исследуется влияние вектора начального приближения к решению и значения допустимой ошибки на сходимость методов и число итераций.
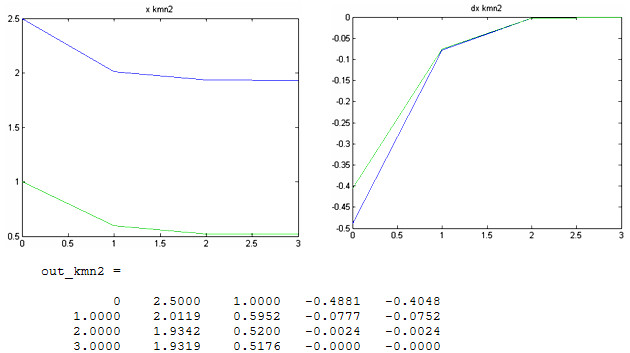
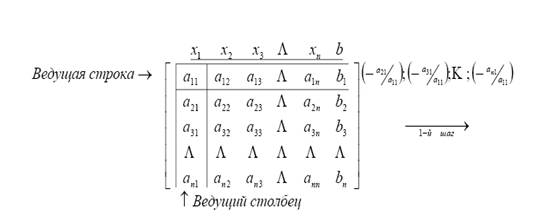
1. Решение системы 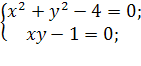 обеими методами, графики решений и ошибок при начальных условиях
обеими методами, графики решений и ошибок при начальных условиях ![]() :
:
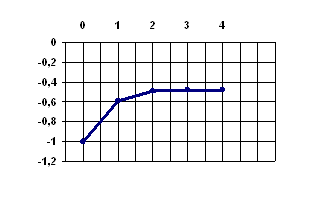
Как и следовало ожидать, метод Ньютона сошелся на две итерации быстрее благодаря квадратичной скорости сходимости.
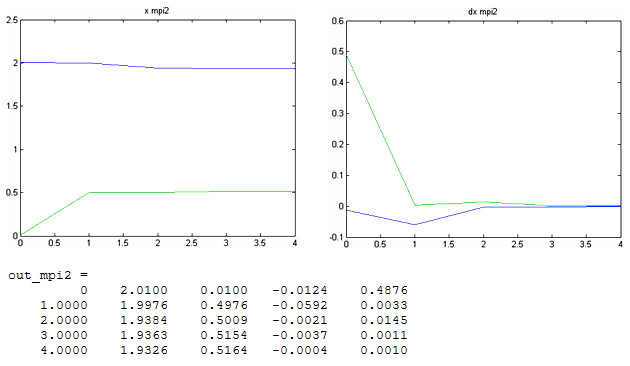
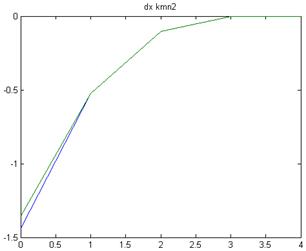
2. При начальных условиях ![]() - начальные условия отстоят от точного решения примерно на 0,5.
- начальные условия отстоят от точного решения примерно на 0,5.
Метод Ньютона опять сошелся быстрее на две итерации, общее число итерации каждого метода по сравнению с предыдущим решением увеличилось на единицу, поэтому можно сделать вывод, что разница между точным решением и начальным приближением 0,5 несущественно повлияла на сходимость.
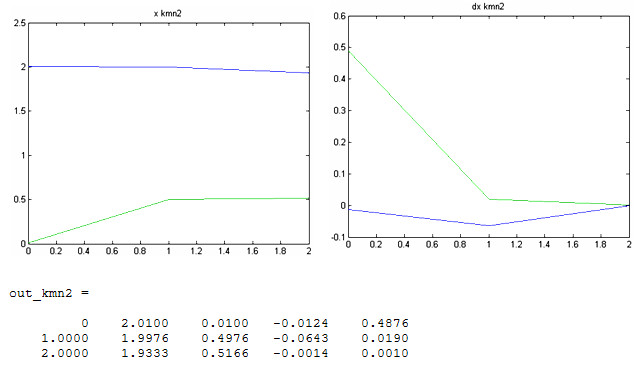
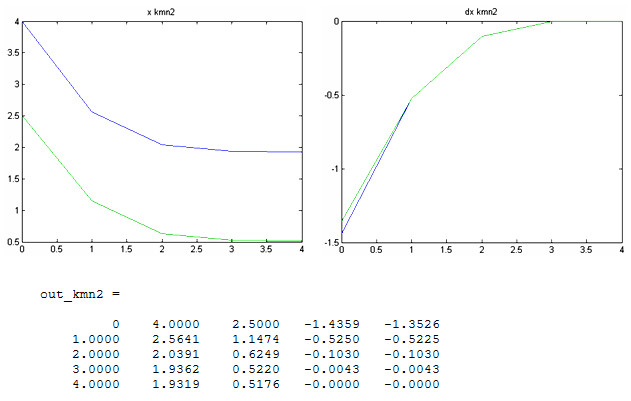
3. При начальных условиях ![]() - начальные условия отстоят от точного решения примерно на 2.
- начальные условия отстоят от точного решения примерно на 2.
Результаты вычислений показывают, что при отстоянии начального приближения от точного значения на 2 количество итераций в методе простой итерации значительно возросло, в то время как число итерации метода Ньютона увеличилось всего на 1.
4. Для проверки времени счета введем в модули методов новую переменную t, определяющую время счета, и возьмем начальные приближение, очень далекие от точного решения ![]() - начальные условия отстоят от точного решения примерно на 37.
- начальные условия отстоят от точного решения примерно на 37.
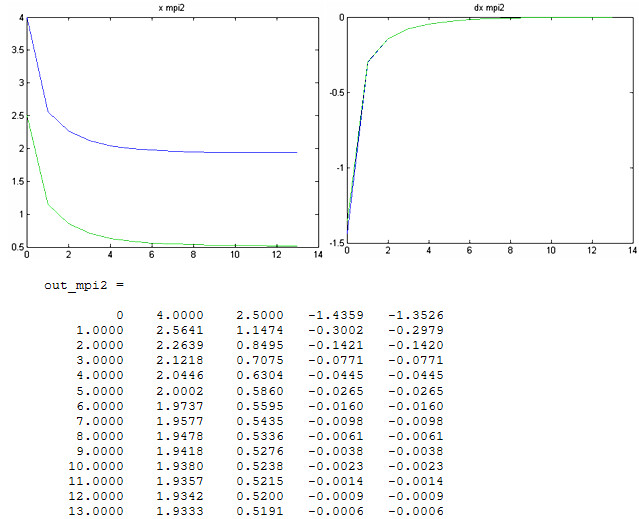
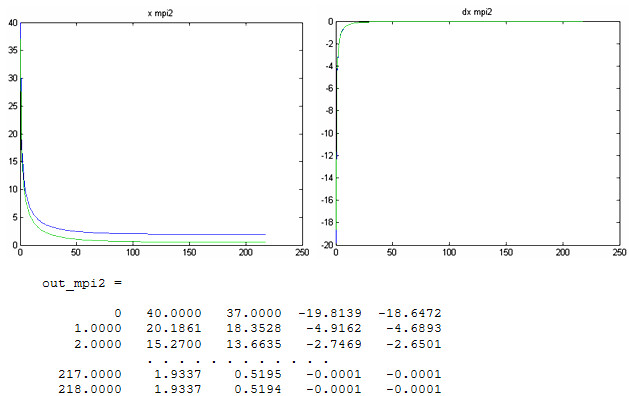
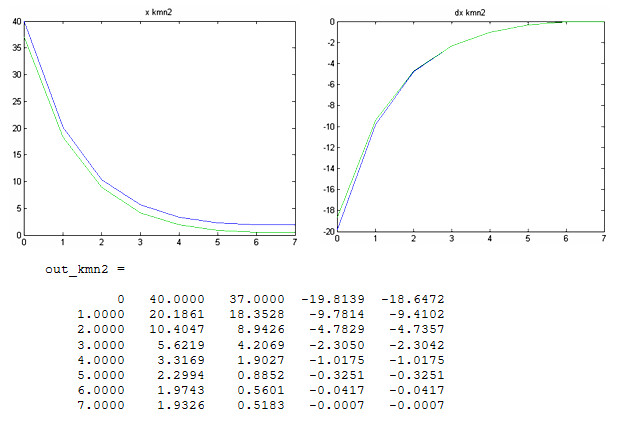
Время в MatLab выводится в формате год/месяц/день/часы/минуты/секунды, то есть метод простой итерации сошелся за 0,015 секунд, а метод Ньютона за время менее 0,00009 секунд (не отображается); число итераций метода простой итерации возросло на 200, метода Ньютона – на единицу. Так как из теории известно, что если метод Ньютона не сходится за 6-7 итераций, то он не сойдется вообще, попытаемся найти такое начальное приближение, при котором этот метод уже не сойдется.
При начальных условиях x0=[1000;500]; edop=0.01 метод итераций сходится уже более чем за минуту и 44 тысячи итераций, а метод Ньютона – за неотображаемое время и 15 итераций. Таким образом, метод итераций хоть и сходится, но требует неадекватных эффективности вычислительных затрат, а метод Ньютона, несмотря на теорию о его несходимости при количестве итераций больше 6-7, сходится, и очень быстро.
Возьмем начальные условия x0=[10000000000; 1500000000], edop=0.01 и решим систему методом Ньютона.
t =0 0 0 0 0 0.0160
То есть метод сошелся за 0,016 секунд, выполнив при этом 35 итераций, и все еще сходится.
Увеличивая начальное приближения до величины порядка 1040, мы все еще получаем сходимость, при количестве итераций порядка 130.
4 Анализ результатов, выводы
Целью нашего исследование было сравнение методов простой итерации и Ньютона для решения систем из двух нелинейных уравнений по числу итераций, времени сходимости в зависимости от выбора начального приближения к решению и допустимой ошибки. Зависимость этих параметров от выбора начального приближения подробно представлена в предыдущем пункте. Проанализировав полученные результаты, можно сказать, что при достаточном удалении от точного решения количество итераций и время счета обоих методов, безусловно, возрастает, но в случае метода простой итерации количество итерации возрастает геометрически относительно метода Ньютона. Мы попытались определить границы сходимости метода Ньютона, но многократные расчеты при достаточно больших начальных приближениях (порядка 1040) не смогли дать ответа на этот вопрос – точное решение достигалось за очень малое (в сравнении со степенью приближений) число итераций – порядка 130.
Сравнив методы по времени счета и количеству итераций при различной точности (в данной работе наглядно не представлено), можно сделать вывод, что метод Ньютона и по этому параметру эффективней метода простой итерации – при допустимой ошибке 10-14 метод простой итерации сошелся за 235 итераций и 0,016 секунд, а метод Ньютона – за 7 итераций и неотобразимо малое время.
Таким образом, сделаем общий вывод: метод Ньютона на порядок эффективней метода простой итерации по таким параметрам, как время счета и число итераций при выборе начального приближения, достаточно далекого от точного решения или при достаточно высокой точности вычислений.
ЗАКЛЮЧЕНИЕ
При выполнении данной работы были рассмотрены теоретически и практически основные характеристики методов простой итерации и Ньютона для решения систем двух нелинейных уравнений.
Мы получили следующие результаты:
· метод простой итерации проще в реализации, чем метод Ньютона – он не требует, в частности, расчета матрицы Якоби на каждом шаге;
· методы сходятся за небольшое количество итераций, если начальное приближение взято близко к точному решению;
· при отдалении начального приближения от точного решения, скорость сходимости и число итераций методов отличаются на порядки, метод Ньютона сходится за гораздо меньшее время и число итераций;
· при очень сильном отдалении от начального решения применение метода простой итерации нецелесообразно ввиду очень больших вычислительных затрат;
· при уменьшении допустимой ошибки вычислительные затраты метода простой итерации значительно больше, чем метода Ньютона, но не так велики, как при увеличении начальных приближений на тот же порядок – то есть изменение точности имеет меньшее влияние на параметры сходимости, чем изменение начального приближения;
Метод Ньютона для решения систем двух нелинейных уравнений оказался более эффективным, чем метод простой итерации по всем рассматриваемым параметрам.
Нам не удалось определить мерность начального приближения, необходимого для того, чтобы метод Ньютона не сошелся.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах.–М.: Наука, 1972. – 368 с.
2. Сарычева О.М. Численные методы в экономике: Конспект лекций /НГТУ –Новосибирск, 1995. – 65 с.
3. Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных систем уравнений со многими неизвестными. – М.:Мир, 1975. – 558 с.
Похожие работы
... точке приближенного решения, т. е. Последовательные приближения (4) строятся по формулам: , (9) где – начальное приближение к точному решению . 4.5 Метод Зейделя на основе линеаризованного уравнения Итерационная формула для построения приближенного решения нелинейного уравнения (2) на основе линеаризованного уравнения (7) имеет вид: 4.6 Метод наискорейшего спуска Методы ...
... . Специалист для которого MS Excel является именно тем средством которое позволяет облегчить и ускорить его работу, должен знать и уметь использовать в повседневной работе новейшие экономико-математические методы и модели, предлагаемые новыми прикладными программами. Традиционный способ изучения экономико-математических методов заключается не только в определении их назначения и сути, ...
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...
... на языке Turbo Pascal 7.0 для решении систем линейных алгебраических уравнений, используя метод простой итерации. 1.2 Математическая формулировка задачи Пусть А – невырожденная матрица и нужно решить систему где диагональные элементы матрицы А ненулевые. 1.3 Обзор существующих численных методов решения задачи Метод Гаусса В методе Гаусса матрица СЛАУ с помощью равносильных ...
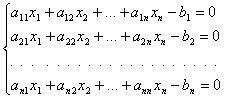
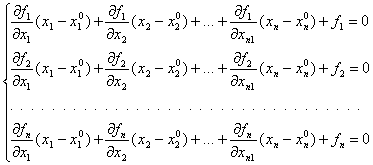
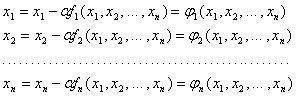
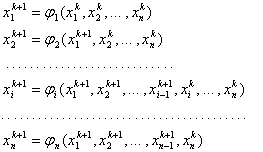
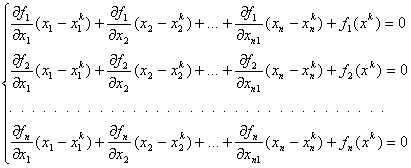


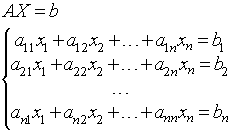
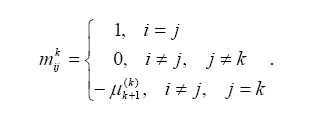
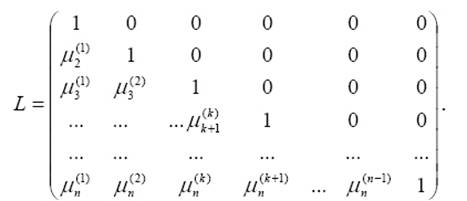
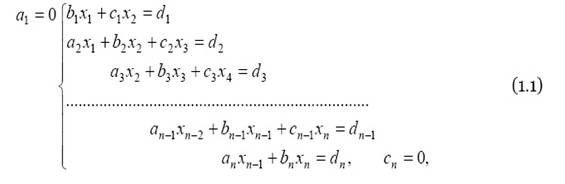
0 комментариев