Закон Кулона. Поле и потенциал распределенной системы зарядов в вакууме

3232

знака

таблицы

изображений

М.И. Векслер, Г.Г. Зегря

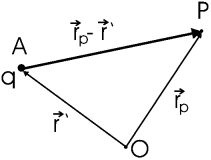
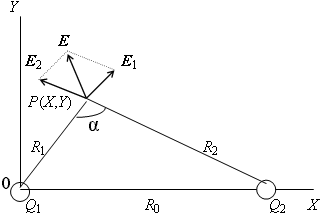
Пусть O - начало координат, P - точка, в которой ищется поле, A - точка, в которой расположен заряд q. Вектор $\vec{OP}$ обычно обозначают $\vec{r}_p$ , вектор $\vec{OA}$ обозначают $\vec{r} '$ . Тогда напряженность электрического поля и потенциал, создаваемые зарядом, записываются как:

$\vec{E} = \frac{q}{4\pi\varepsilon_0} \cdot\frac{(\vec{r}_p-\vec{r} ')}{|\vec{r}_p-\vec{r} '|^3} \varphi = \frac{1}{4\pi\varepsilon_0}\cdot\frac{q} {|\vec{r}_p-\vec{r} '|}$

(1)

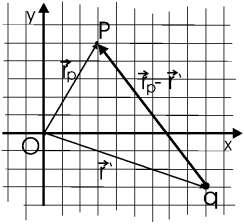
Задача. Найти поле, которое в точке $\vec{r}_p = 3\vec{i}+5\vec{j}$ создает заряд q, находящийся в точке $\vec{r} '=9\vec{i}-3\vec{j}$ .

Ответ: $\vec{E}=\frac{q}{4\pi\varepsilon_0}\cdot\frac{-6\vec{i} +8\vec{j}}{1000}$

При наличии распределенного заряда, создающего поле, необходимо провести интегрирование:

$\vec{E} = \frac{1}{4\pi\varepsilon_0} \int\frac{(\vec{r}_p-\vec{r} ') {\rm d}q}{|\vec{r}_p-\vec{r} '|^3} \varphi = \frac{1}{4\pi\varepsilon_0} \int\frac{{\rm d}q}{|\vec{r}_p-\vec{r} '|}$

(2)

При этом $\vec{r} '$ пробегает всевозможные положения из начала координат в точки, где есть заряд dq. Последний записывается как

${\rm d}q = \left{\begin{array}{ll} \rho {\rm d}V &- {\rm объемный заряд, Kл/cм^3}\\ \sigma {\rm d}S &- {\rm поверхностный заряд, Kл/cм^2}\\ \lambda {\rm d}l &- {\rm линейный заряд, Kл/cм^1}\\ {\rm просто} q &-{\rm точечный заряд (интегрирования нет)} \end{array} \right.$

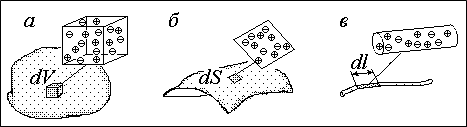
Если рассматривается равномерно заряженная зарядом Q объемная (объема V), поверхностная (площади S) или линейная (длины L) область, то, соответственно,

$\rho = \frac{Q}{V}, \sigma = \frac{Q}{S}, \lambda = \frac{Q}{L}$

(3)

Как записать dV, dS и dl? Это зависит исключительно от геометрии:

${\rm d}V = \left{\begin{array}{ll} {\rm d}x {\rm d}y {\rm d}z &- {\rm элемент объема куба}\\ r^2{\rm d}r\sin\theta {\rm d}\theta {\rm d}\varphi &-{\rm элемент объема шара}\\ {\rm d}r{\rm d}z{\rm d}\varphi &- {\rm элемент объема цилиндра}\\ \end{array} \right.$

${\rm d}S = \left{\begin{array}{ll} {\rm d}x{\rm d}y &- {\rm элемент площади нa плоскости}\\ r{\rm d}r{\rm d}\varphi &- {\rm элемент площади круга}\\ R{\rm d}z{\rm d}\varphi &- {\rm элемент площади боковой поверхности цилиндра}\\ R^2\sin\theta {\rm d}\theta {\rm d}\varphi &- {\rm элемент площади сферы}\\ \end{array} \right.$

${\rm d}l = \left{\begin{array}{ll} {\rm d}x &- {\rm элемент длины на прямой}\\ R{\rm d}\varphi &- {\rm элемент длины окружности}\\ \end{array} \right.$

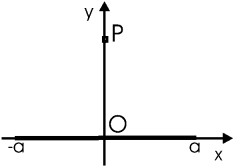
Задача. Нить, равномерно заряженная с плотностью λ0, имеет длину 2a и расположена в плоскости xy вдоль оси x симметрично относительно оси y. Найти поле на оси y как функцию y.

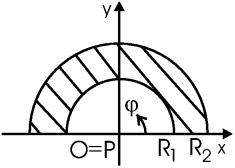
Ответ: $\vec{E}=\frac{\lambda_0a}{2\pi\varepsilon_0y\sqrt{y^2+a^2}} \vec{j}$

Задача. Найти потенциал в центре пластины в форме полудиска. Внутренний и внешний радиусы R1 и R2, заряд σ = σ0sinφ, где φ- угол в плоскости xy.

Решение: Потенциал рассчитываем по стандартной формуле (2):

$\varphi = \frac{1}{4\pi\varepsilon_0} \int\frac{{\rm d}q}{|\vec{r}_p-\vec{r} '|}$

При этом

$\vec{r}_p$	=	$\vec{0}$
$\vec{r} '$	=	$r\cos\varphi\vec{i}+r\sin\varphi\vec{j}$

Соответственно,

$\vec{r}_p-\vec{r} '$	=	$-r\cos\varphi\vec{i}- r\sin\varphi\vec{j}$
$\|\vec{r}_p-\vec{r} '\|$	=	r

С учетом формы тела, создающего поле,

dq = σ(r, φ)· dS = σ0sinφ· rdr dφ

причем φ изменяется в пределах от 0 до π, а r - от R1 до R2. Теперь можно продолжить интегрирование формулы для φ:

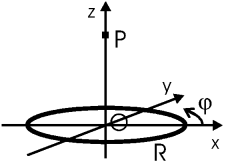
$\varphi = \frac{1}{4\pi\varepsilon_0} \int\limits_{0}^{\pi}\int\limits_{R_1}^{R_2}\frac{\sigma_0\sin \varphi\cdot r{\rm d}r{\rm d}\varphi}{r} = \frac{\sigma_0} {4\pi\varepsilon_0}(R_2-R_1)\cdot 2 = \frac{\sigma_0(R_2-R_1)} {2\pi\varepsilon_0}$

Задача. Найти поле на оси кольца радиуса R, заряженного как λ = λ0cosφ. Кольцо расположено в плоскости xy.

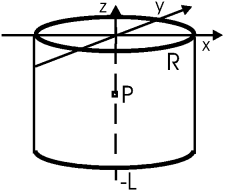
Ответ: $\vec{E}=-\frac{\lambda_0R^2}{4\varepsilon_0 (z^2+R^2)^{3/2}} \vec{i}$

Задача. Найти потенциал на оси z цилиндрической поверхности радиуса R. Цилиндр заряжен как σ = σ0cosφ и расположен соосно с z, занимая область –L... 0.

Ответ: φ(z) = 0

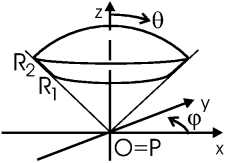
Задача. Найти поле в центре шарового сектора с внутренним и внешним радиусами R1, R2, занимающего область φ = 0... 2π, θ = 0... π/4, равномерно заряженного зарядом ρ0.

Решение: Заряженный объект (шаровой сектор) является объемным, так что

dq = ρ dV = ρ0· r2drsinθdθdφ

где использовано выражение для элемента объема шара. У нас начало координат совпадает с точкой, где ищется поле, так что

$\vec{r}_p = \vec{0}$

Вектор $\vec{r} '$ запишется:

$\vec{r'} = r\sin\theta\cos\varphi\vec{i} +r\sin\theta\sin\varphi\vec{j} +r\cos\theta\vec{k}$

При этом

$\left{\begin{array}{ll} \vec{r}_p-\vec{r} ' &= -r\sin\theta\cos\varphi\vec{i} - r\sin\theta\sin\varphi\vec{j} - r\cos\theta\vec{k}\\ |\vec{r}_p-\vec{r} '| &= r \end{array} \right.$

Теперь у нас уже есть все составные компоненты для проведения интегрирования. Пределы интегрирования вытекают из условия задачи:

$\vec{E}$	=	$\frac{1}{4\pi\varepsilon_0} \int\frac{(\vec{r}_p-\vec{r} ') {\rm d}q}{\|\vec{r}_p-\vec{r} '\|^3} = \frac{1}{4\pi\varepsilon_0}\cdot$
		$\cdot\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi/4} \int\limits_{R_1}^{R_2}\frac{-r\sin\theta\cos\varphi\vec{i}- r\sin\theta\sin\varphi\vec{j}-r\cos\theta\vec{k}}{r^3}\cdot \rho_0\cdot r^2 \mbox{d}r \sin\theta\mbox{d}\theta\mbox{d}\varphi$

Совершенно очевидно, что члены, содержащие cosφ или sin φ, при интегрировании по φ от 0 до 2π дадут ноль (это интегрирование по периоду), поэтому их можно дальше не выписывать.

$\vec{E}$	=	$\frac{1}{4\pi\varepsilon_0} \int\limits_{0}^{2\pi}\int\limits_{0}^{\pi/4}\int\limits_{R_1}^{R_2} \frac{-r\cos\theta\vec{k}}{r^3}\cdot \rho_0\cdot r^2{\rm d}r\sin \theta{\rm d}\theta{\rm d}\varphi=$
	=	$-\frac{1}{4\pi\varepsilon_0}\cdot (R_2-R_1)\cdot 2\pi \cdot\rho_0\cdot \int\limits_{0}^{\pi/4}\cos\theta\sin\theta{\rm d} \theta\cdot\vec{k} =$
	=	$-\frac{1}{4\pi\varepsilon_0}\cdot (R_2-R_1)\cdot 2\pi \cdot\rho_0\cdot \left.\frac{\sin^2\theta}{2}\right\|_0^{\pi/4}\cdot\vec{k} = -\frac{\rho_0(R_2-R_1)}{8\varepsilon_0}\vec{k}$

Направление вектора $\vec{E}$ против оси z естественно из симметрии задачи. Если заряд положителен, то поле должно быть ориентировано от заряженного сектора, что и имеет место.

Список литературы

1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.

2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.

3. Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика. т.8 Электродинамика сплошных сред, 2-е изд., М.: Наука, 1992. - 661 с.

Для подготовки данной работы были использованы материалы с сайта http://edu.ioffe.ru/r

Раздел: Математика
Количество знаков с пробелами: 3232
Количество таблиц: 22
Количество изображений: 7

Скачать

... выражений, (3) и (10). Эта операция позволяет также частично избавиться от проблем, связанных с характеристиками поля на небольших расстояниях от точечных зарядов, и с трудностями учёта собственных полей зарядов в теории [1, 5, 10]. Таким образом, взаимодействие зарядов определяется только членом W3, зависящим от силовых характеристик обоих зарядов одновремённо. Аналогом объёмного интеграла от W3 ...

Скачать

... , олова, ртути, свинца), а также ряда сплавов скачком падает до нуля. Это явление получило название сверхпроводимости. Это явление не может быть объяснено на основе классической электронной теории проводимости. Объяснение этому явлению дает только квантовая механика. Классическая электронная теория проводимости оказалась не в состоянии объяснить зависимость сопротивления металлов от температуры ...

Скачать

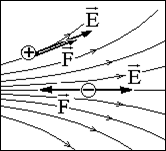
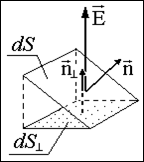
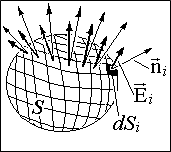
... уходят в бесконечность. На рис. (1.2.3) в соответствии с картиной силовых линий показаны векторы напряженности и силы, действующей на заряды разного знака. 3 Поток напряженности электрического поля. Теорема Гаусса в интегральной форме Пусть n – единичная нормаль к площадке dS (достаточно малой, чтобы пренебречь изменением электрической напряженности Е в пределах площадки). Поток dФэ ...

Скачать

... представляют собой проявление одного и того же фундаментального принципа. Эйнштейн опередил свое время. В то время, когда он жил, еще не было известно сильное и слабое взаимодействие, поэтому он так и не смог выстроить Единую Теорию Поля. Больше того, его поиски в то время были мало понятны большинству физиков - почти все из них были озабочены разработкой новой дисциплины - квантовой механикой. ...

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

Похожие работы

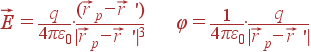
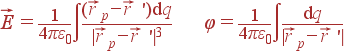
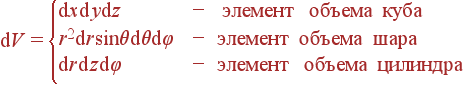
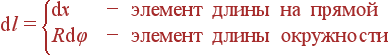
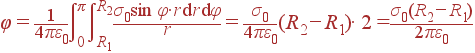
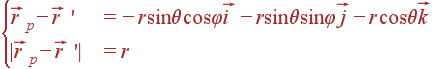
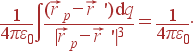
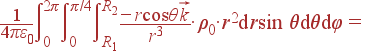
0 комментариев

Разделы

Инфо

Следите за новостями