Навигация
1.2. Метод Зейделя
1.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений
Ax = b
с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду
x = Bx + c.
Здесь B – квадратная матрица с элементами bij (i, j = 1, 2, …, n), c – вектор-столбец с элементами cij (i = 1, 2, …, n).
В развернутой форме записи система имеет следующий вид:
x1 = b11x1 + b12x2 + b13x3 + … + b1nxn + c1
x2 = b21x1 + b22x2 + b23x3 + … + b2nxn + c2
. . . . . . . . . . . . . . . . .
xn = bn1x1 + bn2x2 + bn3x3 + … + bnnxn + cn
Вообще говоря, операция приведения системы к виду, удобному для итераций, не является простой и требует специальных знаний, а также существенного использования специфики системы.
Самый простой способ приведения системы к виду, удобному для итераций, состоит в следующем. Из первого уравнения системы выразим неизвестное x1:
x1 = a11–1 (b1 – a12x2 – a13x3 – … – a1nxn),
из второго уравнения – неизвестное x2:
x2 = a21–1 (b2 – a22x2 – a23x3 – … – a2nxn),
и т. д. В результате получим систему
x1 = b12x2 + b13x3 + … + b1,n–1xn–1 + b1nxn+ c1 ,
x2 = b21x1 + b23x3 + … + b2,n–1xn–1 + b2nxn+ c2 ,
x3 = b31x1 + b32x2 + … + b3,n–1xn–1 + b3nxn+ c3 ,
. . . . . . . . . . . . . . . . . . . . . . .
xn = bn1x1 + bn2x2 + bn3x3 + … + bn,n–1xn–1 + cn ,
в которой на главной диагонали матрицы B находятся нулевые элементы. Остальные элементы выражаются по формулам
bij = –aij / aii, ci = bi / aii (i, j = 1, 2, …, n, j ≠ i)
Конечно, для возможности выполнения указанного преобразования необходимо, чтобы диагональные элементы матрицы A были ненулевыми.
1.2.1. Описание метода. Введем нижнюю и верхнюю треугольные матрицы
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0 0 0 … 0 0 b12 b13 … b1n
0 0 0 … 0 0 b12 b13 … b1n
b21 0 0 … 0 0 0 b23 … b2n
B1 = b31 b32 0 … 0 , B2 = 0 0 0 … b3n
. . . . . . . . . . . . . .
![]()
![]()
![]()
![]() bn1 bn2 bn3 … 0 0 0 0 … 0
bn1 bn2 bn3 … 0 0 0 0 … 0
Заметим, что B = B1 + B2 и поэтому решение x исходной системы удовлетворяет равенству
x = B1x + B2 x + c .
Выберем начальное приближение x(0) = [x1(0), x2(0), …, xn(0)]T. Подставляя его в правую часть равенства при верхней треугольной матрице B2 и вычисляя полученное выражение, находим первое приближение
x(1) = B1x(0) + B2x(1)
Подставляя приближение x(1), получим
x(2) = B1x(1) + B2x(2)
Продолжая этот процесс далее, получим последовательность x(0), x(1), …, x(n), … приближений к вычисляемых по формуле
x(k+1) = B1(k+1) + B2(k) + c
или в развернутой форме записи
x1(k+1) = b12x2(k) + b13x2(k) + … + b1nxn(k) + c1 ,
x2(k+1) = b21x1(k+1) + b23x3(k) + … + b2nxn(k) + c2 ,
x3(k+1) = b31x1(k+1) + b32x2(k+1) + … + b3nxn(k) + c3 ,
. . . . . . . . . . . . . . . . . . . . . . . . . .
xn(k+1) = bn1x1(k+1) + bn2x2(k+1) + bn3x3(k+1) + … + cn .
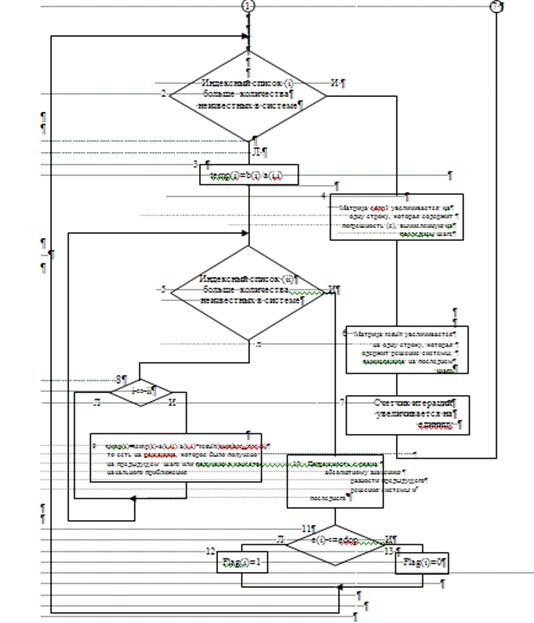
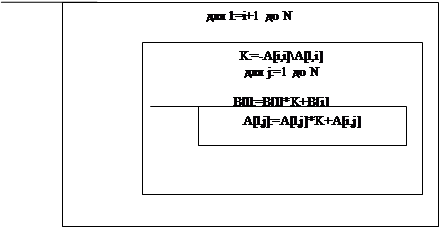
Объединив приведение системы к виду, удобному для итераций и метод Зейделя в одну формулу, получим
xi(k+1) = xi(k) – aii–1(∑j=1i–1 aijxj(k+1) + ∑j=1n aijxi(k) – bi).
Тогда достаточным условием сходимоти метода Зейделя будет
∑j=1, j≠i n | aij | < | aii |
(условие доминированния диагонали).
Метод Зейделя иногда называют также методом Гаусса-Зейделя, процессом Либмана, методом последовательных замещений.
1.3. Сравнение прямых и итерационных методов
Системы линейных алгебраических уравнений можно решать как с помощью прямых, так и и итерационных методов. Для систем уравнений средней размерности чаще использют прямые методы.
Итерационные методы применяют главным образом для решения задач большой размерности, когда использование прямых методов невозможно из-за ограниченииий в доступной оперативной памяти ЭВМ или из-за необходимости выполнения черезмерно большого числа арифметических операций. Большие системы уравнений, возникающие в основном в приложениях, как правило являются разреженными. Методы исключения для систем с разреженным и матрицами неудобны, например, тем, что при их использовании большое число нулевых элементов превращается в ненулевые и матрица теряет свойство разреженности. В противоположность им при использованнии итерационных методов в ходе итерационного процесса матрица не меняется, и она, естественно, остается разреженной. Большая эффективность итерационных методов по сравнению с прямыми методами тесно связанна с возможностью существенного использования разреженности матриц.
Применение итерационных методов для качественного решения большой системы уравнений требует серьезного использования ее структуры, специальных знаний и определенного опыта.
2. Практическая часть
2.1 Программа решения систем линейных уравнений по методу Гаусса
2.1.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида
a11x1 + a12x2 + … + a1nxn = b1 ,
a21x2 + a22x2 + … + a2nxn = b2 ,
. . . . . . . . . . . . .
an1x1 + an2x2 + … + annxn = bn
для n ≤ 10 по методу Гаусса.
Похожие работы
... , но выбор перехода к системе x=(x) зависит от типа конкретной решаемой системы линейных алгебраических уравнений. 6. Заключение В данной курсовой работе был реализован метод простой итерации для решения систем линейных алгебраических уравнений в виде двух программ, каждая из которых использует свой собственный способ перехода от системы вида F(x)=x к системе вида x=(x). Вообще говоря, ...
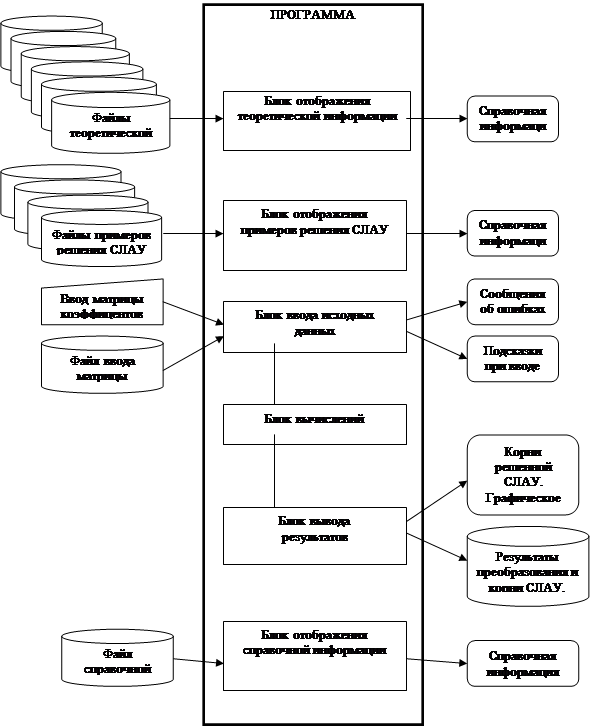
... Рисунок 1.1 - Схема информационных потоков для вычисления СЛАУ методом Гаусса Условные обозначения к рисунку 2.1: - данные, вводимые с клавиатуры - данные, хранящиеся на диске - данные, выводимые на экран 2. Решение систем линейных алгебраических уравнений методом гаусса 2.1 Основные понятия Система линейных алгебраических уравнений (СЛАУ) из m уравнений с n неизвестными ...
... 1.2 0.4 -0.8 -0.8 3.6 4 4.7 10.4 9.7 9.7 -8.4Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = ...
... линейных уравнений: Или в матричном виде: , где матрица коэффициентов системы; - вектор неизвестных; - вектор свободных членов. 2. Точные методы решения СЛАУ Метод главных элементов. Пусть дана система линейных алгебраических уравнений. Рассмотрим расширенную матрицу, состоящую из коэффициентов системы a[i,j] и свободных членов b[i]. Метод главных элементов - это обобщение ...




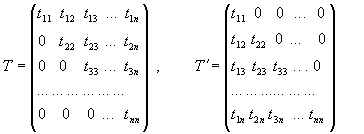
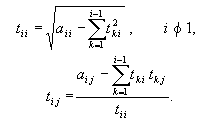
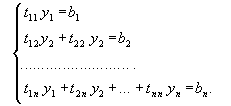
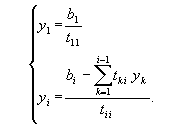
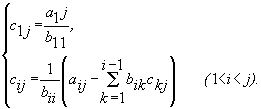
0 комментариев