Задание 1
Вычислите 
и 
последовательности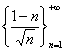 
.
Решение.
Рассмотрим последовательность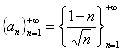 
.
для любого натурального 
Следовательно, множество 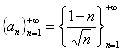является ограниченным сверху. Это означает, что последовательность 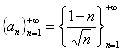имеет верхнюю точную грань: 
.
Следовательно, множество 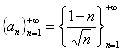не является ограниченным снизу. Это означает, что нижняя грань 
последовательности 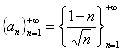не существует.
Ответ.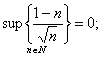 
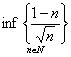не существует
Задание 2
Пользуясь определением предела последовательности, докажите, что 
.
Доказательство.
Число 
называется пределом последовательности 
, если для любого положительного числа 
существует номер 
такой, что при 
выполняется неравенство 
.
Используя определение предела последовательности, докажем, что .
Возьмем любое число 
.
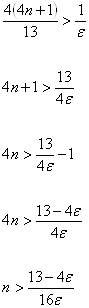
Если взять 
, то для всех будет выполняться неравенство 
. Следовательно, .
Доказано
Задание 3
Пользуясь определением предела функции, докажите, что 
.
Доказательство
Число 
называется пределом функции 
при 
, если для любого числа существует число 
такое, что для всех 
, удовлетворяющих неравенству 
, выполняется неравенство 
.
Используя определение предела функции, докажем, что .
Возьмем любое .
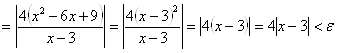
Положим 
.
Если взять , то для всех 
, удовлетворяющих неравенству 
, выполняется неравенство 
. Следовательно, .
Доказано.
Задание 4
Вычислите предел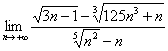 
.
Решение.
Ответ. 
Задание 5
Вычислите предел 
.
Решение.
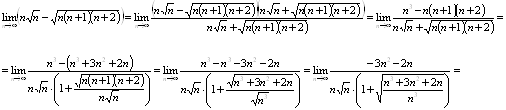
Ответ. 
Задание 6
Вычислить предел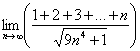 
.
Решение.
Ответ. 
Задание 7
Вычислить предел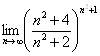 
.
Решение.
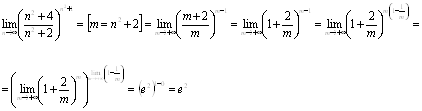
Ответ. 
Задание 8
Вычислить предел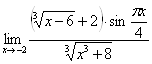 
.
Решение
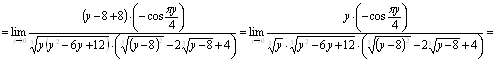
Ответ. 
Задание 9
Вычислить предел 
.
Решение.
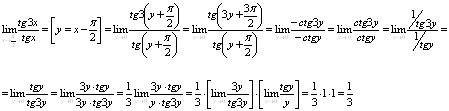
Ответ. 
Задание 10
Вычислить предел 
.
Решение.
Ответ. 
Задание 11
Вычислить предел 
.
Решение.
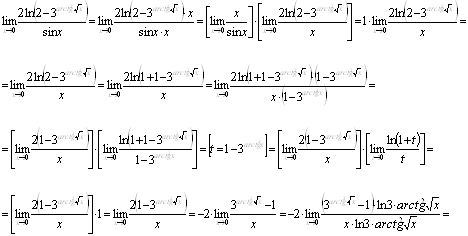
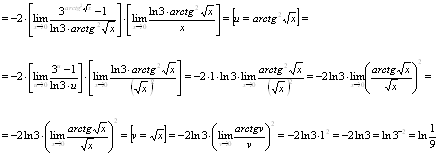
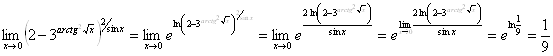
Ответ. 
Задание 12
Вычислить предел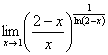 
.
Решение.
Ответ.
Задание 13
Вычислить предел 
.
Решение.
Ответ. 
Задание 14
Вычислить предел 
.
Решение.
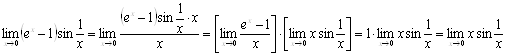
при 
функция 
является бесконечно малой
для любого 
функция 
является ограниченной.
Известно, что произведение бесконечно малой функции и ограниченной функции есть бесконечно малая функция. Следовательно, функция 
является бесконечно малой при . Это означает, что 
.
Ответ. 
Похожие работы
ывают определением на «языке последовательностей». Второе определение носит название «на языке ». Кроме понятия предела функции в точке, существует также понятие предела функции при стремлении аргумента к бесконечности: число А называется пределом функции при , если для любого числа существует такое число d, что при всех справедливо неравенство : . Теоремы о пределах функций являются базой для ...
... , они делят область определения функции на три промежутка: Исследуемая функция в промежутке – возрастает – убывает - возрастает 5. Найдем промежутки выпуклости графика функции, ее точки перегиба. Найдем вторую производную функции: при - точка перегиба Для , следовательно, график функции на этом интервале выпуклый вверх. Для , следовательно, график ...
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
... , не надо» (т.е. ее математические эквиваленты) усваивается хуже, чем напыщенное «Если вам это и не нравится, то придется вам это проглотить». Я рекомендовал бы ставить после «если» «то» во всех математических текстах. Наличие слова «то» никогда не приведет к недоразумению, а вот его отсутствие — может. Последняя техническая деталь, которая может помочь в писательской работе, и которую здесь ...
0 комментариев