Доказательство великой теоремы Ферма для четных показателей степени

Файл: FERMA-2mPF-for

© Н. М. Козий, 2007

Авторские права защищены свидетельствами Украины

№ 27312 и № 28607

 

ДОКАЗАТЕЛЬСТВО ВЕЛИКОЙ ТЕОРЕМЫ ФЕРМА ДЛЯ ЧЕТНЫХ ПОКАЗАТЕЛЕЙ СТЕПЕНИ

 

Великая теорема Ферма формулируется следующим образом: диофантово уравнение(http://soluvel.okis.ru/evrika.html):

 

Аⁿ+ Вⁿ= Сⁿ /1/

где n- целое положительное число, большее двух, не имеет решения в целых положительных числах.

Суть Великой теоремы Ферма не изменится, если уравнение /1/ запишем следующим образом:

 

Аⁿ= Сⁿ -Вⁿ  /2/

Пусть показатель степени n=2m. Тогда уравнение /2/ запишется следующим образом:

 

А^2m= С^2m –В^2m /3/

Для доказательства великой теоремы Ферма используем алгебраическое доказательство теоремы Пифагора.

АЛГЕБРАИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПИФАГОРА (Решение уравнения теоремы Пифагора в целых числах)

 

Теорема Пифагора формулируется следующим образом: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

 

С² =А² + В², /4/

где: С – гипотенуза; А и В – катеты.

Существуют прямоугольные треугольники, у которых стороны А, В и С выражаются целыми числами. Такие числа называются пифагоровыми.

Рассматривая уравнение теоремы Пифагора как алгебраическое уравнение, докажем, что существует бесконечное количество прямоугольных треугольников, в которых их стороны выражаются целыми числами или, что одно и тоже, уравнение /4/ имеет бесконечное количество решений в целых числах.

Суть теоремы Пифагора не изменится, если уравнение /4/ запишем следующим образом:

 

А² = С² –В² /5/

Для доказательства теоремы Пифагора методами элементарной алгебры используем два известные в математике метода решения алгебраических уравнений: метод решения параметрических уравнений и метод замены переменных.

Уравнение /5/ рассматриваем как параметрическое уравнение с параметром A и переменными B и С. Уравнение /5/ в соответствии с известной зависимостью для разности квадратов двух чисел запишем в виде:

 

А²=(C-B)∙(C+B) /6/

Используя метод замены переменных, обозначим:

 

C-B=M /7/

Из уравнения /7/ имеем:

 

C=B+M /8/

Из уравнений /6/, /7/ и /8/ имеем:

 

А² =M∙ (B+M+B)=M∙(2B+M) = 2BM+M² /9/

Из уравнения /9/ имеем:

 

А²- M²=2BM /10/

Отсюда: B = /11/

Из уравнений /8/ и /11/ имеем:

C= 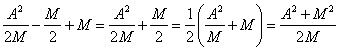 /12/

Таким образом: B = /13/

C  /14/

Из уравнений /11/ и /12/ следует, что необходимым условием для того чтобы числа В и С были целыми, является делимость числа A² на число M , т. е. число M должно быть одним из сомножителей, входящих в состав сомножителей числа А или A².

Числа А и M должны иметь одинаковую четность.

По формулам /13/ и /14/ определяются числа B и C как переменные, зависящие от значения числа А как параметра и значения числа M.

Из изложенного следует: 1. Квадрат простого числа A равен разности квадратов одной пары чисел B и C (при M=1). 2. Квадрат составного числа A равен разности квадратов одной пары или нескольких пар чисел B и C. 3. Квадрат числа A^m равен разности квадратов нескольких пар чисел. 4. Все числа A> 2 являются пифагоровыми.

Таким образом, существует бесконечное количество троек пифагоровых чисел А, В и С и, следовательно, бесконечное количество прямоугольных треугольников, у которых стороны А, В и С выражаются целыми числами.

ДОКАЗАТЕЛЬСТВО ВЕЛИКОЙ ТЕОРЕМЫ ФЕРМА

Вариант 1

 

Уравнение /3/ с учетом уравнений /5/ и /6/ запишем следующим образом:

 

А^2m= С^2m –В^2m =(С^m –В^m)∙(С^m +В^m) /15/

Тогда в соответствии с уравнениями /13/ и /14/ запишем:

 

B^m = /16/

C^m /17/

Из уравнений /16/ и /17/ следует, что необходимым условием для того чтобы числа В и С были целыми, является делимость числа A^2m на число M , т. е. число M должно быть одним из сомножителей, входящих в состав сомножителей числа А или A^2m. Следовательно, число A^2m должно быть равно:

 

A^2m = M· D, /18/

где D – целое число.

Тогда : B^m = /19/

А число C^m с учетом уравнения /8/ равно:

 

C^m = B^m + M =  /20/

Тогда из уравнений /19/ и /20/ следует:

 

B = 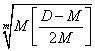 /21/

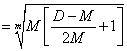C  /22/

Если допустить, что В – целое число, то из уравнения /22/ следует, что число С не может быть целым числом, так как сомножители в скобках в подкоренных выражениях в уравнениях /21/ и /22/ отличаются всего на 1.

 

ДОКАЗАТЕЛЬСТВО ВЕЛИКОЙ ТЕОРЕМЫ ФЕРМА

Вариант 2

Выше в доказательстве теоремы Пифагора доказано, что все натуральные числа являются пифагоровыми. Следовательно, все натуральные числа распределяются на тройки пифагоровых чисел и, следовательно, все тройки пифагоровых чисел удовлетворяют уравнению /4/:

 

С² =А² + В² /23/

Пифагоровы числа (А, В, С) могут быть истолкованы как длины сторон прямоугольного треугольника, а их квадраты могут быть истолкованы как площади квадратов, построенных на гипотенузе и катетах этого треугольника. Умножив приведенное уравнение на С, получим:

 

С³=А²∙ С+ В²· С /24/

Из уравнения /24/ следует, что объем куба раскладывается на два объема двух параллелепипедов. Поскольку очевидно, что в уравнении /23/ А<C и В<C, то из уравнения /24/ следует:

 

С³>А³ + В³ /25/

На всем множестве троек пифагоровых чисел ( а все натуральные числа образуют тройки пифагоровых чисел) при показателе степени n=3 не может быть ни одного решения уравнения /1/:

 

Аⁿ+ Вⁿ= Сⁿ

Следовательно, на всем множестве натуральных чисел невозможно куб разложить на два куба.

Умножив уравнение /23/ на С², получим:

 

С²∙С² =А²·С² + В²∙С² /26/

Все члены этого уравнения представляют собой объемы параллелепипедов:

параллелепипед С²∙С² имеет в основании квадрат со стороной С и высоту С²;

параллелепипед А²∙С² имеет в основании квадрат со стороной А и высоту С²;

параллелепипед В²∙С² имеет в основании квадрат со стороной В и высоту С².

Следовательно, в соответствии с уравнением /26/ объем одного параллелепипеда разложился на сумму объемов двух параллелепипедов.

Поскольку, как показано выше, А<C и В<C, то из уравнения /26/ следует:

 

С⁴>А⁴ + В⁴ /27/

В общем случае уравнение /26/ можно записать следующим образом:

 

С²∙С^n-2=А²·С^n-2 + В²∙С^n-2 /28/

Сⁿ=А²·С^n-2 + В²∙С^n-2 /29/

Следовательно, в соответствии с уравнениями /28/ и /29/ объем одного параллелепипеда разложился на сумму объемов двух параллелепипедов. Поскольку, как показано выше, А<C и В<C, то из уравнения /29/ следует:

 

Сⁿ>Аⁿ+ Вⁿ /30/

 

Таким образом, великая теорема Ферма не имеет решения в целых положительных числах при четных показателях степени.