Практическая работа
На тему: «Вычисление наибольшего, наименьшего значения функции в ограниченной области»
Цель
1. Ознакомление и приобретение навыков вычисления наибольшего, наибольшего значения функции в ограниченной области.
Основные вопросы:
1.Наибольшее и наименьшее значение функции.
2.Ограниченная область.
3.Равномерно непрерывная функция.
Если функция f(x, y, …) определена и непрерывна в замкнутой и ограниченной области D, то в этой области найдется, по крайней мере, одна точка
N(x0, y0, …), такая, что для остальных точек верно неравенство
f(x0, y0, …) ³ f(x, y, …)
а также точка N1(x01, y01, …), такая, что для всех остальных точек верно неравенство
f(x01, y01, …) £ f(x, y, …)
тогда f(x0, y0, …) = M – наибольшее значение функции, а f(x01, y01, …) = m – наименьшее значение функции f(x, y, …) в области D.
Непрерывная функция в замкнутой и ограниченной области D достигает по крайней мере один раз наибольшего значения и один раз наименьшего.
Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой ограниченной области D, а M и m – соответственно наибольшее и наименьшее значения функции в этой области, то для любой точки m Î [m, M] существует точка
N0(x0, y0, …) такая, что f(x0, y0, …) = m.
Проще говоря, непрерывная функция принимает в области D все промежуточные значения между M и m. Следствием этого свойства может служить заключение, что если числа M и m разных знаков, то в области D функция по крайней мере один раз обращается в ноль.
Свойство. Функция f(x, y, …), непрерывная в замкнутой ограниченной области D, ограничена в этой области, если существует такое число К, что для всех точек области верно неравенство ![]()
Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой ограниченной области D, то она равномерно непрерывна в этой области, т.е. для любого положительного числа e существует такое число D > 0, что для любых двух точек (х1, y1) и (х2, у2) области, находящихся на расстоянии, меньшем D, выполнено неравенство
![]()
Точки, в которых функция принимает наибольшее или наименьшее значения в ограниченной замкнутой области, называют также точками абсолютного или глобального экстремума. Если наибольшее или наименьшее значения достигаются во внутренних точках области, то это точки локального экстремума функции z = f ( x , y ) . Таким образом точки, в которых функция принимает наибольшее или наименьшее значения являются либо локальными экстремумами, либо граничными точками области. Следовательно, чтобы найти наибольшее и наименьшее значения функции z = f ( x , y ) в ограниченной замкнутой области D, следует вычислить значение функции в критических точках области D, а также наибольшее и наименьшее значения функции на границе. Если граница задана уравнением ϕ ( x , y ) = 0 , то задача отыскания наибольшего и наименьшего значений функции на границе области D сводится к отысканию наибольшего и наименьшего значений (абсолютного экстремума) функции одной переменной, так как уравнение границы области D - ϕ ( x , y ) = 0 связывает переменные x и y между собой. Значит, если разрешить уравнение ϕ ( x , y ) = 0 относительно одной из переменных или параметрические уравнения границы области D и подставить их в уравнение z = f ( x , y ) , то придем к задаче нахождения наибольшего и наименьшего значений функции одной переменной. Если уравнение ϕ ( x , y ) = 0 невозможно разрешить относительно одной из переменных или невозможно найти параметрическое задание границы, то задача сводится к отысканию условного экстремума.
Правило нахождения наибольшего и наименьшего значений дифференцируемой в области D функции z = ƒ(х;у) состоит в следующем:
1. Найти все критические точки функции, принадлежащие D , и вычислить значения функции в них;
2. Найти наибольшее и наименьшее значения функции z = ƒ(х;у) на границах области;
3. Сравнить все найденные значения функции и выбрать из них наибольшее М и наименьшее.
Задачи:
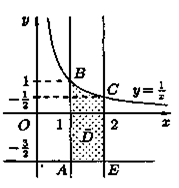
1. Найти наибольшее и наименьшее значения функции z=х2у + ху2 + ху в замкнутой области, ограниченной линиями: у = 1/x, х = 1, х = 2, у = -1,5
Решение: Здесь z'x=2ху+у2+у, z'y=х2+2ху+х.
Находим все критические точки:
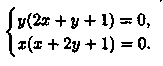
Решением системы являются точки (0;0), (-1;0), (0; -1),(-1/3;-1/3). Ни одна из найденных точек не принадлежит области D .
2. Исследуем функцию z на границе области, состоящей из участков АВ, ВС, СЕ и ЕА
На участке АВ:
![]()
![]()
Значения функции z(-1) = -1,
![]()
На участке ВС:
![]()
![]()
Значения функции z(1) = 3, z(2) = 3,5.
На участке СЕ:
![]()
z'y=4у+6, 4у+6=0, у=-3/2.
Значения функции
![]()
![]()
На участке АЕ:
![]()
![]()
Значения функции z(1) = -3/4,z(2) = -4,5.
3. Найти наибольшее M и наименьшее m значения функции z = 4x2-2xy+y2-8x в замкнутой области D, ограниченной: x = 0, y = 0, 4x+3y=12 .
Решение
1. Построим область D (рис. 1.5) на плоскости Оху.
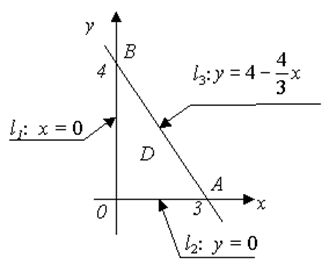
Угловые точки: О (0; 0), В (0; 4), А (3; 0).
Граница Г области D состоит из трёх частей:
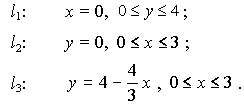
Примеры:
1. Найти наибольшее и наименьшее значения функции z = х2у + ху2 + ху в замкнутой области, ограниченной линиями: х = 1, х = 2, у = 1,5
2. Найти наибольшее и наименьшее значения функции z = 2 x 3 − 6 xy + 3 y 2 в замкнутой области D, ограниченной осью OY, прямой y = 2 и параболой y = x 2 при x ≥ 0 .
3. Найти наибольшее M и наименьшее m значения функции z = 4x2-2xy+y2-8x в замкнутой области D, ограниченной: x = 0, y = 0, 4x+3y=12 .
4. Найти наибольшее и наименьшее значения функции z=х2у + ху2 + ху в замкнутой области, ограниченной линиями: у = 1/x, х = 1, х = 2, у = -1,5
5. Найти наибольшее и наименьшее значения функции ![]() в треугольнике, ограниченном прямыми
в треугольнике, ограниченном прямыми ![]() ,
, ![]() ,
, ![]() .
.
Похожие работы
... при построении итерационных методов решения уравнения =0. Например взяв за корень линейного интерполяционного алгебраического многочлена, построенного по значениям и в узле или по значениям и в узлах и , приходят соответственно к методу Ньютона и метода секущих , где - разделенная разность функций для узлов и . Другой подход к построению численных методов решения уравнения ...
... векторы в силу (6.8) оказались бы линейно зависимыми .Разделив обе части на 0 получим равенство вида (6.9). ч.т.д. Пример №5. Пусть требуется найти экстремум функции u=xyzt при условии x+y+z+t=4c; область изменения переменных определяетссся неравенствовами x>0, y>0, t>0, z>0. Применяя к этой задаче метод Лагранжа, введем вспомогательную ...
... Для U = f(x,y, z) в точке Мо (хо ,уо, zо) будет выполнено условие . Замечание. Точку, в которой частные производные первого порядка либо не существуют, либо равны нулю, называют критической. Т.е. экстремумы функции нескольких переменных могут достигаться лишь в критических точках. Пример 15.1. Покажем, что указанные выше условия не являются достаточными. Пусть z = f(x, y) = x × y тогда ...
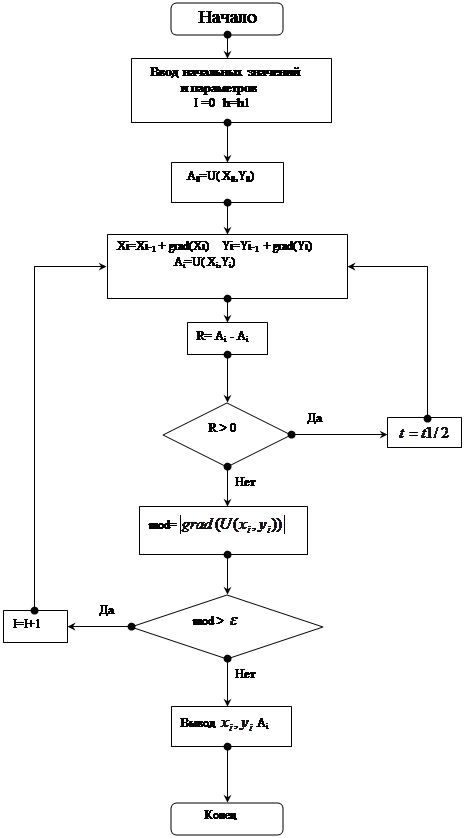
... и градиент функции вычисляется в меньшем числе точек. Описание программы Программа предназначена для нахождения точек минимума функций нескольких переменных – другими словами для минимизации этих функций. В программе реализован один из методов спуска – Градиентный метод спуска с выбором шага. Начальный шаг задается. Изменение шага осуществляется по схеме если ; если Вычисление ...


0 комментариев