Навигация
МЕХАНИКА СПЛОШНОЙ СРЕДЫ
ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
1. Сохранение массы. Уравнение неразрывности
Материальный континуум обладает свойством, называемым массой. Суммарная масса некоторой части сплошной среды, занимающей в момент t объем пространства V, выражается интегралом
![]() (1.1)
(1.1)
где ![]() - непрерывная функция координат, называемая плотностью. Закон сохранения массы, утверждает, что масса выделенной части среды остается постоянной и, следовательно, материальная производная от (1.1) равна нулю. Если в формуле (4.52) положить P'ij. (x, t) ss р (х, 0, то получим выражение для скорости изменения массы т
- непрерывная функция координат, называемая плотностью. Закон сохранения массы, утверждает, что масса выделенной части среды остается постоянной и, следовательно, материальная производная от (1.1) равна нулю. Если в формуле (4.52) положить P'ij. (x, t) ss р (х, 0, то получим выражение для скорости изменения массы т
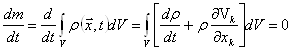 (1.2)
(1.2)
Поскольку это равенство верно для произвольного объема V, подинтегральное выражение само должно обращаться в нуль, т. е.
![]() или
или ![]() (1.3)
(1.3)
Это уравнение называется уравнением неразрывности (или непрерывности). Раскрывая оператор материальной производной, его можно написать в другой равнозначной форме
![]() , или
, или ![]() (1.4)
(1.4)
В несжимаемой среде плотность массы каждой частицы не зависит от времени, т. е. ![]() , и уравнение (1.3) принимает вид
, и уравнение (1.3) принимает вид
![]() , или
, или ![]() . (1.5)
. (1.5)
Поле скорости ![]() в несжимаемой среде можно поэтому представить выражением
в несжимаемой среде можно поэтому представить выражением
![]() или
или ![]() , (1.6)
, (1.6)
где функция ![]() называется векторным потенциалом
называется векторным потенциалом ![]() .
.
Уравнение неразрывности можно записывать в лагранжевой, или материальной, форме. Для сохранения массы требуется, чтобы выполнялось уравнение
![]() . (1.7)
. (1.7)
Здесь оба интеграла взяты по одним и тем же частицам, т. е. V - это объем, который теперь занимает среда, заполнявшая в момент t = 0 объем ![]() . Используя (4.1) и (4.38), интеграл в правой части (1.7) можно преобразовать следующим образом:
. Используя (4.1) и (4.38), интеграл в правой части (1.7) можно преобразовать следующим образом:
![]() (1.8)
(1.8)
Соотношение (1.8) должно иметь силу для произвольно выбранного объема ![]() , и поэтому
, и поэтому
![]() (1.9)
(1.9)
Это означает, что произведение ![]() не зависит от времени, так как объем V произволен, т. е. что
не зависит от времени, так как объем V произволен, т. е. что
![]() (1.10)
(1.10)
Уравнение (1.10) является лагранжевой дифференциальной формой уравнения неразрывности.
2. Теорема об изменении количества движения. Уравнения движения
Уравнения равновесия
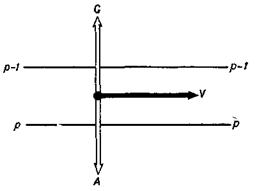
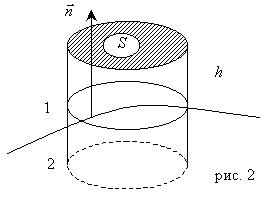
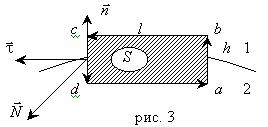
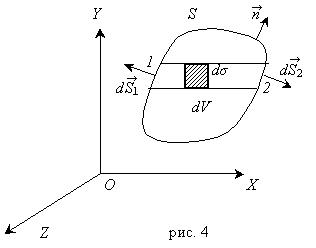
На рис. 2.1 изображен движущийся объем сплошной среды V в момент t. На него действуют массовые силы с плотностью распределения ![]() . На каждом бесконечно малом элементе
. На каждом бесконечно малом элементе ![]() поверхности, ограничивающей рассматриваемый объем, действует вектор напряжения
поверхности, ограничивающей рассматриваемый объем, действует вектор напряжения ![]() . Во всей области, занятой средой, определено поле скоростей
. Во всей области, занятой средой, определено поле скоростей ![]() . Общее количество движения системы масс, заполняющих объем V, определяется интегралом
. Общее количество движения системы масс, заполняющих объем V, определяется интегралом
![]() . (2.1)
. (2.1)
Основываясь на втором законе Ньютона, теорема об изменении количества движения утверждает, что скорость изменения со временем количества движения некоторой части континуума равна результирующей сил, действующих на рассматриваемую область. Если внутренние силы, действующие между частицами данного объема (рис. 2.1), подчиняются третьему закону Ньютона о действии и противодействии, то теорема об изменении количества движения для этой системы масс выражается уравнением
![]() ,
,
или (2.2)
![]() .
.
После подстановки ![]() в первый интеграл и преобразования интеграла по поверхности в интеграл по объему (согласно теореме Гаусса — Остроградского) это уравнение примет вид
в первый интеграл и преобразования интеграла по поверхности в интеграл по объему (согласно теореме Гаусса — Остроградского) это уравнение примет вид
![]()
или (2.3)
![]()
Распишем материальную производную правой части (2.3) и воспользуемся уравнением неразрывности в форме (1.10). Это даст
 . (2.4)
. (2.4)
Подстановка этого выражения в правую часть (2.3) и объединение членов приводят к интегральной форме теоремы об изменении количества движения:
![]()
или (2.5)
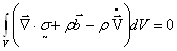
Так как объем V произволен, само подинтегральное выражение (2.5) должно обращаться в нуль. Полученные таким образом уравнения
![]() , или
, или ![]() (2.6)
(2.6)
называются уравнениями движения.
Для случая равновесия, когда отсутствуют ускорения, из (2.6) получаются уравнения, называемые уравнениями равновесия
![]() , или
, или ![]() (2.7)
(2.7)
Похожие работы
... тензора внутренних напряжений в идеальной жидкости (газе) имеет вид: , (2.6) и тензор P целиком определяется скаляром p. Понятно, что идеальная жидкость не единственно возможная модель сплошной среды, позволяющая определить компоненты тензора внутренних напряжений. Можно, например, рассматривать его компоненты как функции от деформации частицы: в этом случае среда называется упругой. В ...
... состояние равновесия – на поверхность тела действует сила давления жидкости, которая уравновешивает вес жидкости внутри поверхности. Движение жидкостей и газов. Движение жидкостей и газов, как и все другие виды движения, рассматриваемые в механике, можно полностью охарактеризовать, оперируя единицами измерения длины, времени и силы. Так, диаметр парашюта можно измерять в метрах, время ...
... Так как на практике почти всегда приходится решать уравнения Максвелла (1) – (4) в кусочно-непрерывных средах, то граничные условия (24) следует рассматривать как неотъёмлемую часть уравнений Максвелла (1) – (4). В случае стационарных электрических и магнитных полей ( и) система уравнений Максвелла (1) – (4) распадается на систему уравнений электростатики: , , ...
... как правило, не могут быть найдены теоретически, поэтому для оценок интенсивности и спектрального состава звука используют различные модели турбулентного движения[13,15]. 2.2 Краткая история акустики движущихся сред В науке сформировалось новое самостоятельное направление, получавшее название аэроакустики. Зародившаяся на стыке двух наук — аэродинамики и классической акустики, она связана с ...
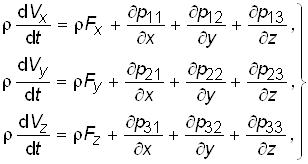

0 комментариев