Федеральное агентство по образованию Российской Федерации
Государственное образовательное учреждение
Высшего профессионального образования
Владимирский Государственный Университет
Доклад
по теории кодирования
на тему:
Теория кодирования в среде MATLAB
Владимир 2010
Пакет Communications Toolbox
Применяется научными, коммерческими и военными организациями для разработки новых алгоритмов кодирования, шифрования, модуляции и передачи данных с учетом различных эффектов искажения и интерференции. Ключевые возможности
Средства вычислений в конечных полях Галуа.
Средства визуализации сигналов: глазковая диаграмма, сигнальное созвездие и др.
Специальные средства визуализации нестационарных параметров канала.
Средства вычисления, анализа и сравнения коэффициента битовой ошибки (BER).
Готовые функции и средства разработки алгоритмов кодирования источника, помехоустойчивого кодирования, перемежения, модуляции, демодуляция и эквализации.
Генерация проверочной и порождающей матриц для кода Хэмминга
Синтаксис:
h = hammgen(m); h = hammgen(m,pol); [h,g] = hammgen(...); [h,g,n,k] = hammgen(...);
Описание:
Для всех вариантов синтаксиса длина кодового слова обозначается как n. Величина n равна 2m – 1 для некоторого целочисленного m, большего или равного трем. Длина блока исходного сообщения обозначается как k, она равна n – m.
Пример:
Приведенная ниже команда выводит на экран проверочную и порождающую матрицы для кода Хэмминга с длиной кодового слова 7 = 23 – 1 и длиной блока исходного сообщения 4 = 7 – 3.
[h,g,n,k] = hammgen(3)
h = 1 0 0 1 0 1 1 0 1 0 1 1 1 0 0 0 1 0 1 1 1 g = 1 1 0 1 0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 1 0 1 0 1 0 0 0 1 n = 7 k = 4
Следующая команда использует явно заданный примитивный полином 1 + x2 + x3, показывая тем самым, что вид проверочной матрицы зависит от выбора примитивного полинома. Чтобы в этом убедиться, сравните выведенную ниже матрицу h1 с матрицей h из предыдущего примера.
h1 = hammgen(3,[1 0 1 1])
h1 = 1 0 0 1 1 1 0 0 1 0 0 1 1 1 0 0 1 1 1 0 1
Генерация порождающего полинома для циклического кода
Синтаксис:
pol = cyclpoly(n,k); pol = cyclpoly(n,k,opt);
Описание:
Для всех вариантов синтаксиса полином представляется в виде строки, содержащей коэффициенты полинома в порядке возрастания степеней.
pol = cyclpoly(n,k)
Возвращает вектор-строку, представляющий один из нетривиальных порождающих полиномов для циклического кода с длиной кодового слова n и длиной блока исходного сообщения k.
pol = cyclpoly(n,k,opt)
Производит поиск одного или нескольких нетривиальных порождающих полиномов для циклических кодов с длиной кодового слова n и длиной блока исходного сообщения k. Результат pol зависит от входного параметра opt.
Пример:
Первая из приведенных ниже команд дает представления для трех порождающих полиномов циклического кода (15, 4).
Вторая команда показывает, что порождающим полиномом с максимальным весом (числом ненулевых коэффициентов) является 1 + x + x2 + x3+ x5+ x7+ x8+ x11.
Третья команда демонстрирует, что для циклического кода (15, 4) не существует порождающих полиномов с весом (числом ненулевых коэффициентов), равным трем.
c1 = cyclpoly(15,4,'all') c1 = 1 1 0 0 0 1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 1 1 1 1 1 1 1 1 0 1 0 1 1 0 0 1 c2 = cyclpoly(15,4,'max') c2 = 1 1 1 1 0 1 0 1 1 0 0 1 c3 = cyclpoly(15,4,3) No generator polynomial satisfies the given constraints. c3 = []
Генерация проверочной и порождающей матриц для циклического кода
Синтаксис:
parmat = cyclgen(n,pol); parmat = cyclgen(n,pol,opt); [parmat,genmat] = cyclgen(...); [parmat,genmat,k] = cyclgen(...);
Описание:
n - длина кодового слова
k - размер блока исходного сообщения.
Полином может породить циклический код с длиной кодового слова n и размером блока исходного сообщения k тогда и только тогда, когда этот полином имеет степень (n – k) и является делителем полинома xn – 1. (В двоичном конечном поле GF(2) xn – 1 — это то же самое, что и xn + 1.) Отсюда следует, что k равняется n минус степень порождающего полинома. Входной параметр opt определяет, должна итоговая матрица соответствовать систематическому или несистематическому коду.
Пример:
pol = cyclpoly(7,4); [parmat,genmat,k] = cyclgen(7,pol) parmat = 1 0 0 1 1 1 0 0 1 0 0 1 1 1 0 0 1 1 1 0 1 genmat = 1 0 1 1 0 0 0 1 1 1 0 1 0 0 1 1 0 0 0 1 0 0 1 1 0 0 0 1 k = 4
>> [parmat,genmat,k]= cyclgen(7,cyclpoly(7,4),'nonsys')
parmat =
1 1 1 0 1 0 0
0 1 1 1 0 1 0
0 0 1 1 1 0 1
genmat =
1 0 1 1 0 0 0
0 1 0 1 1 0 0
0 0 1 0 1 1 0
0 0 0 1 0 1 1
k =
4
//полученная проверочная матрица соответствует несистематическому циклическому коду
Преобразование порождающей матрицы в проверочную и обратно
Синтаксис:
parmat = gen2par(genmat); genmat = gen2par(parmat);
Описание:
parmat = gen2par(genmat)
Преобразует двоичную порождающую матрицу genmat, представленную в стандартной форме, в соответствующую проверочную матрицу parmat.
genmat = gen2par(parmat)
Преобразует двоичную проверочную матрицу parmat, представленную в стандартной форме, в соответствующую порождающую матрицу genmat.
Пример:
Приведенные ниже команды преобразуют проверочную матрицу для кода Хэмминга в соответствующую порождающую матрицу и обратно.
parmat = hammgen(3)
parmat =
1 0 0 1 0 1 1 0 1 0 1 1 1 0 0 0 1 0 1 1 1
genmat = gen2par(parmat)
genmat =
1 1 0 1 0 0 0 0 1 1 0 1 0 0 1 1 1 0 0 1 0 1 0 1 0 0 0 1
parmat2 = gen2par(genmat) % Результат должен быть равен parmat
parmat2 =
1 0 0 1 0 1 1 0 1 0 1 1 1 0 0 0 1 0 1 1 1
Расчет кодового расстояния для линейного блокового кода
Синтаксис:
wt = gfweight(genmat); wt = gfweight(genmat,'gen'); wt = gfweight(parmat,'par'); wt = gfweight(genpoly,n);
Описание:
Кодовое расстояние для линейного блокового кода равно минимальному числу различающихся элементов в произвольной паре кодовых слов.
wt = gfweight(genmat)
Возвращает кодовое расстояние для линейного блокового кода с порождающей матрицей genmat.
wt = gfweight(genmat,'gen')
Возвращает кодовое расстояние для линейного блокового кода с порождающей матрицей genmat.
wt = gfweight(parmat,'par')
Возвращает кодовое расстояние для линейного блокового кода с проверочной матрицей parmat.
wt = gfweight(genpoly,n)
Возвращает кодовое расстояние для циклического кода с длиной кодового слова n и порождающим полиномом genpoly. Параметр genpoly должен быть вектором-строкой, содержащим коэффициенты порождающего полинома в порядке возрастания степеней.
Пример:
Приведенные ниже команды показывают три способа вычисления кодового расстояния для циклического кода (7,4).
n = 7; % Порождающий полином для циклического кода (7,4) genpoly = cyclpoly(n,4)
genpoly =
1 0 1 1
>> [parmat, genmat] = cyclgen(n,genpoly)
parmat =
1 0 0 1 1 1 0
0 1 0 0 1 1 1
0 0 1 1 1 0 1
genmat =
1 0 1 1 0 0 0
1 1 1 0 1 0 0
1 1 0 0 0 1 0
0 1 1 0 0 0 1 wts = [gfweight(genmat,'gen'), gfweight(parmat,'par'), gfweight(genpoly,n)] wts =
3 3 3
Генерация таблицы зависимости векторов ошибок от синдрома (таблицы декодирования) для двоичных кодов
Синтаксис:
t = syndtable(parmat);
Описание:
t = syndtable(parmat)
Возвращает таблицу декодирования для двоичного корректирующего кода с длиной кодового слова n и длиной сообщения k. Параметр parmat — проверочная матрица кода, имеющая (n – k) строк и n столбцов. Результат t — двоичная матрица, содержащая 2n – k строк и n столбцов. r-я строка матрицы t представляет собой вектор ошибок для принятого двоичного кодового слова, синдром декодирования которого имеет десятичное целочисленное значение r – 1. (Синдром декодирования равен произведению принятого кодового слова и транспонированной проверочной матрицы.) Иными словами, строки матрицы t представляют собой лидеры смежных классов (coset leaders) из стандартного расположения (standard array) для данного кода.
Пример:
Для кода Хэмминга (7, 4).
m = 3; n = 2^m-1; k = n-m; parmat = hammgen(m) % Проверочная матрица parmat =
1 0 0 1 0 1 1
0 1 0 1 1 1 0
0 0 1 0 1 1 1
trt = syndtable(parmat) % Таблица декодирования trt =
0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0
Пусть принятое кодовое слово - [1 1 0 1 1 0 0]
Путем умножения проверочной матрицы на транспонированное кодовое слово вычисляется синдром декодирования.
parmat*[1;1;0;1;1;0;0]
ans =
2
3
1
В двоичной системе счисления получили – [0 1 1]. Десятичное значение синдрома 3. Соответствующий вектор ошибок, таким образом, следует брать из четвертой (3 + 1) строки таблицы декодирования:
trt(4,:)
ans =
0 0 0 0 1 0 0
Итак следует инвертировать пятый разряд принятого кодового слова –
[1 1 0 1 0 0 0]
Похожие работы
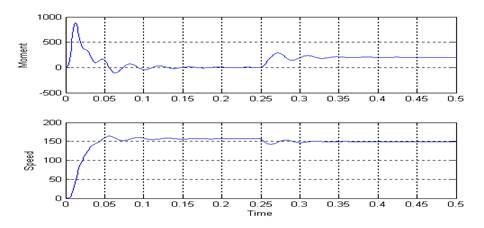
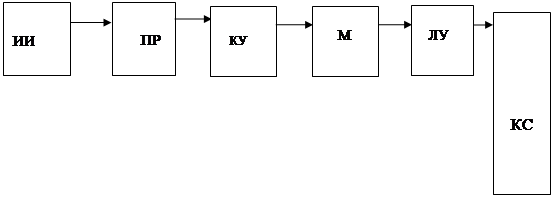
... при механических, климатических и специальных воздействиях окружающей среды; - специальные требования по защите информации. Построение «автоматизированной системы информационной поддержки наладочных работ электропривода» Дано: 1 Объект информатизации 2 Ограничения 3 Критерий 4 База данных 5 Классификатор характеристик 6 Пакет программ ...
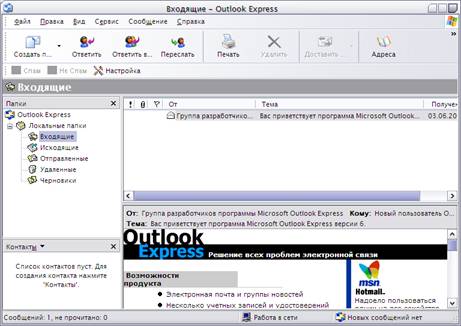
... книги и т.д.). 2. Технологическая часть 2.1. Определение метода сбора данных 2.1.1. Описание стадий сбора данных Определение проблемы. В чем состоит цель исследования почтовых клиентов? Цель исследования состоит в выявлении среди наиболее популярных на сегодняшний день почтовых клиентов наилучшего, обладающего набором функций, оптимальным для пользователя. Необходима ли ...
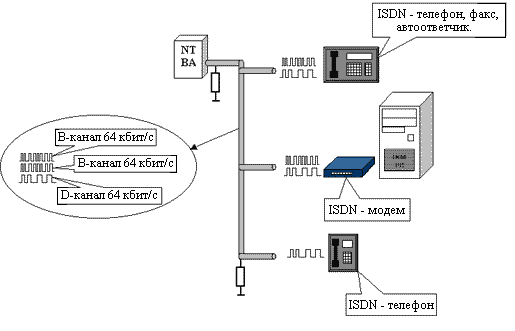
... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...
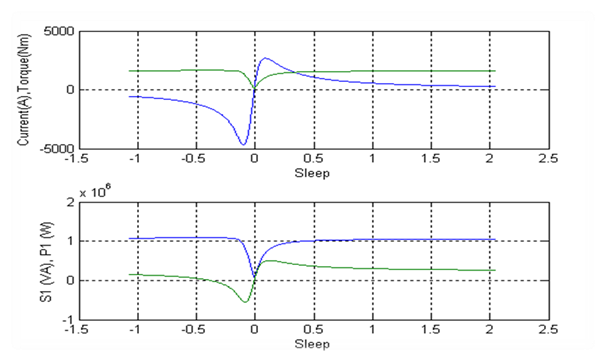
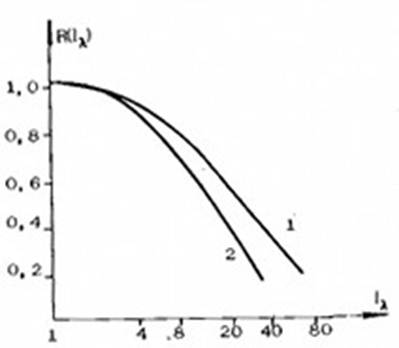
... при работе в условиях нестационарного канала связи; - оптимизация существующих методов получения результирующего сигнала по параметру простота реализации. Научная новизна. 1. Выполнено сравнение основных способов пространственно разнесенного приема в декаметровом канале связи. 2. Получены зависимости качественных показателей пространственно разнесенного приема от величины линейного ...


0 комментариев