Задача №1 (Симплекс метод решения задачи линейного программирования.)
Найти Fmax = 9x1+ 10x2 + 16x3, при ограничениях:

Запишем задачу в каноническом виде:
F=9x1+ 10x2 + 16x3 → max

Заполним начальную таблицу:
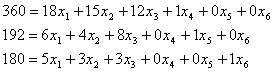
Таблица 0.
| 0 | 9 | 10 | 16 | 0 | 0 | 0 | Отношение, θ | |||
| i |
| Базис |
|
|
|
|
|
|
| |
| 1 | 0 |
| 360 | 18 | 15 | 12 | 1 | 0 | 0 | 30 |
| 2 | 0 |
| 192 | 6 | 4 | 8 | 0 | 1 | 0 | 24 |
| 3 | 0 |
| 180 | 5 | 3 | 3 | 0 | 0 | 1 | 60 |
| ∆j | 0 | -9 | -10 | -16 | 0 | 0 | 0 | |||
| Zj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
Zj вычисляется по формуле ![]()
Оценки (∆j) вычисляются по формуле ![]() , где
, где ![]() - коэффициент из первой строки таблицы.
- коэффициент из первой строки таблицы.
Выбираем минимальную (отрицательную) оценку. Она определяет направляющий столбец.
Заполняем столбец «θ», по минимальному значению определяем направляющую строку.
На пересечение строки и столбца находится направляющий элемент.
Заполняем новую таблицу
Таблица 1.
| 0 | 9 | 10 | 16 | 0 | 0 | 0 | Отношение, θ | |||
| i |
| Базис |
|
|
|
|
|
|
| |
| 1 | 0 |
| 72 | 9 | 9 | 0 | 1 |
| 0 | 8 |
| 2 | 16 |
| 24 |
|
| 1 | 0 |
| 0 | 48 |
| 3 | 0 |
| 108 |
|
| 0 | 0 | - | 1 | 72 |
| ∆j | 384 | 3 | -2 | 0 | 0 | 2 | 0 | |||
| Zj | 384 | 12 | 8 | 0 | 0 | 2 | 0 | |||
Изменяется базис в позиции направляющей строки. Базисным становится вектор, соответствующий направляющему столбцу, т. е. ![]()
Столбец ![]() становится базисным, то есть единичным.
становится базисным, то есть единичным.
Новые значения в направляющей строке получаем делением элементов этой строки на направляющий элемент.
Остальные элементы в небазисных столбцах и в столбце ![]() вычисляем по правилу треугольника.
вычисляем по правилу треугольника.
Выбираем минимальную отрицательную оценку. Она определяет направляющий столбец.
Заполняем столбец «θ»
По минимальному значению определяем направляющую строку.
На пересечении направляющей строки и столбца находится направляющий элемент.
Заполнение второй таблицы осуществляется по аналогии с предыдущей.
Таблица 2.
| 0 | 9 | 10 | 16 | 0 | 0 | 0 | Отношение, θ | |||
| i |
| Базис |
|
|
|
|
|
|
| |
| 1 | 10 |
| 8 | 1 | 1 | 0 |
| - | 0 | ______ |
| 2 | 16 |
| 20 |
| 0 | 1 | - |
| 0 | ______ |
| 3 | 0 |
| 96 |
| 0 | 0 |
| - | 1 | ______ |
| ∆j | 400 | 5 | 0 | 0 |
|
| 0 | |||
| Zj | 400 | 14 | 10 | 16 |
|
| 0 | |||
Так как нет отрицательных оценок ∆j, значит выполняется признак оптимальности и не вводились искусственные переменные, то получено оптимальное решение.
Ответ:
Максимальное значение функции Fmax =400 достигается в точке с координатами:
![]() =0
=0
![]() =8
=8
![]() =20
=20
![]() =0
=0
![]() =0
=0
![]() =96
=96
Задача №2 (Метод Литтла)
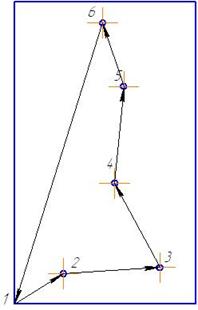
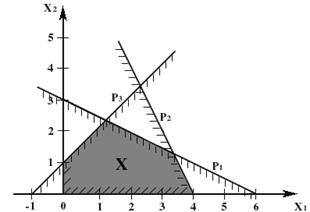
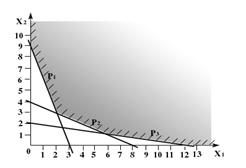
Найти кратчайший путь в графе, заданном графически в виде чертежа, методом Литтла.

Из чертежа запишем матрицу расстояний. (Расстояние от т.1 до т.2 равно:
![]() , и т.д.)
, и т.д.)
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ∞ | 18,87 | 49,48 | 51,86 | 80,51 | 97,42 |
| 2 | 18,87 | ∞ | 32,06 | 34,48 | 65,15 | 84,01 |
| 3 | 49,48 | 32,06 | ∞ | 31,76 | 61,19 | 83,20 |
| 4 | 51,86 | 34,48 | 31,76 | ∞ | 32,14 | 53,15 |
| 5 | 80,51 | 65,15 | 61,19 | 32,14 | ∞ | 22,14 |
| 6 | 97,42 | 84,01 | 83,20 | 53,15 | 22,14 | ∞ |
Предположим что кратчайший путь будет следующим:
т.1→ т.2→ т.3→ т.4→ т.5→ т.6→т.1 и составит ![]()
Решение: Первый этап.
Шаг 1. Приведем матрицу расстояний по строкам и столбцам
(в строке вычитаем из каждого элемента минимальный, затем в столбцах)
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | ∞ | 18,87 | 49,48 | 51,86 | 80,51 | 97,42 | 18,87 |
| 2 | 18,87 | ∞ | 32,06 | 34,48 | 65,15 | 84,01 | 18,87 |
| 3 | 49,48 | 32,06 | ∞ | 31,76 | 61,19 | 83,20 | 31,76 |
| 4 | 51,86 | 34,48 | 31,76 | ∞ | 32,14 | 53,15 | 31,76 |
| 5 | 80,51 | 65,15 | 61,19 | 32,14 | ∞ | 22,14 | 22,14 |
| 6 | 97,42 | 84,01 | 83,20 | 53,15 | 22,14 | ∞ | 22,14 |
↓
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ∞ | 0 | 30,61 | 32,99 | 61,64 | 78,55 |
| 2 | 0 | ∞ | 13,19 | 15,61 | 46,28 | 65,14 |
| 3 | 17,72 | 0,30 | ∞ | 0 | 29,43 | 51,44 |
| 4 | 20,10 | 2,72 | 0 | ∞ | 0,38 | 21,39 |
| 5 | 58,37 | 43,01 | 39,05 | 10,00 | ∞ | 0 |
| 6 | 75,28 | 61,87 | 61,06 | 31,01 | 0 | ∞ |
| 0 | 0 | 0 | 0 | 0 | 0 |
↓
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ∞ | 0 | 30,61 | 32,99 | 61,64 | 78,55 |
| 2 | 0 | ∞ | 13,19 | 15,61 | 46,28 | 65,14 |
| 3 | 17,72 | 0,30 | ∞ | 0 | 29,43 | 51,44 |
| 4 | 20,10 | 2,72 | 0 | ∞ | 0,38 | 21,39 |
| 5 | 58,37 | 43,01 | 39,05 | 10,00 | ∞ | 0 |
| 6 | 75,28 | 61,87 | 61,06 | 31,01 | 0 | ∞ |
Шаг 2. Определим оценки нулевых клеток:
![]()
![]()
![]()
![]()
![]()
![]()
Шаг 3. Вычеркиваем клетку с максимальной оценкой. Включаем данную клетку в путь обхода. (5 – 6)

Шаг 4. Переписываем матрицу расстояний, накладывая запрет на одну из клеток для исключения преждевременного замыкания контура (в клетку 6-5 ставим ∞).
| 1 | 2 | 3 | 4 | 5 | |
| 1 | ∞ | 0 | 30,61 | 32,99 | 61,64 |
| 2 | 0 | ∞ | 13,19 | 15,61 | 46,28 |
| 3 | 17,72 | 0,30 | ∞ | 0 | 29,43 |
| 4 | 20,10 | 2,72 | 0 | ∞ | 0,38 |
| 6 | 75,28 | 61,87 | 61,06 | 31,01 | ∞ |
Далее повторяем шаги 1 – 4, пока не дойдем до одной клетки.
Второй этап.
Шаг 1. Приведем матрицу расстояний по строкам и столбцам.
| 1 | 2 | 3 | 4 | 5 | |
| 1 | ∞ | 0 | 30,61 | 32,99 | 61,64 |
| 2 | 0 | ∞ | 13,19 | 15,61 | 46,28 |
| 3 | 17,72 | 0,30 | ∞ | 0 | 29,43 |
| 4 | 20,10 | 2,72 | 0 | ∞ | 0,38 |
| 6 | 75,28 | 61,87 | 61,06 | 31,01 | ∞ |
| 0 | 0 | 0 | 0 | 0,38 |
↓
| 1 | 2 | 3 | 4 | 5 | |
| 1 | ∞ | 0 | 30,61 | 32,99 | 61,26 |
| 2 | 0 | ∞ | 13,19 | 15,61 | 45,90 |
| 3 | 17,72 | 0,30 | ∞ | 0 | 29,05 |
| 4 | 20,10 | 2,72 | 0 | ∞ | 0 |
| 6 | 75,28 | 61,87 | 61,06 | 31,01 | ∞ |
Шаг 2. Определим оценки нулевых клеток:
![]()
![]()
![]()
![]()
![]()
![]()
Шаг 3. Вычеркиваем клетку с максимальной оценкой. Включаем данную клетку в путь обхода. (1 – 2)

Шаг 4. Переписываем матрицу расстояний, накладывая запрет на одну из клеток для исключения преждевременного замыкания контура (в клетку 2 – 1 ставим ∞).
| 1 | 3 | 4 | 5 | |
| 2 | ∞ | 13,19 | 15,61 | 45,90 |
| 3 | 17,72 | ∞ | 0 | 29,05 |
| 4 | 20,10 | 0 | ∞ | 0 |
| 6 | 75,28 | 61,06 | 31,01 | ∞ |
Третий этап.
Шаг 1. Приведем матрицу расстояний по строкам и столбцам.
| 1 | 3 | 4 | 5 | |
| 2 | ∞ | 13,19 | 15,61 | 45,90 |
| 3 | 17,72 | ∞ | 0 | 29,05 |
| 4 | 20,10 | 0 | ∞ | 0 |
| 6 | 75,28 | 61,06 | 31,01 | ∞ |
| 17,72 | 0 | 0 | 0 |
↓
| 1 | 3 | 4 | 5 | ||
| 2 | ∞ | 13,19 | 15,61 | 45,90 | 13,19 |
| 3 | 0 | ∞ | 0 | 29,05 | 0 |
| 4 | 2,38 | 0 | ∞ | 0 | 0 |
| 6 | 57,56 | 61,06 | 31,01 | ∞ | 31,01 |
↓
| 1 | 3 | 4 | 5 | |
| 2 | ∞ | 0 | 2,42 | 32,71 |
| 3 | 0 | ∞ | 0 | 29,05 |
| 4 | 2,38 | 0 | ∞ | 0 |
| 6 | 26,55 | 30,05 | 0 | ∞ |
Шаг 2. Определим оценки нулевых клеток:
![]()
![]()
![]()
![]()
![]()
Шаг 3. Вычеркиваем клетку с максимальной оценкой. Включаем данную клетку в путь обхода. (4 – 5)
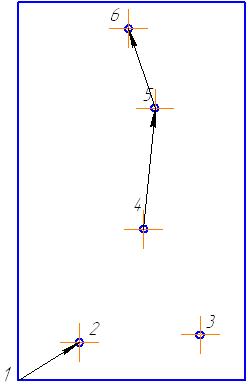
Шаг 4. Переписываем матрицу расстояний, накладывая запрет на одну из клеток для исключения преждевременного замыкания контура (в клетку 6 – 4 ставим ∞).
| 1 | 3 | 4 | |
| 2 | ∞ | 0 | 2,42 |
| 3 | 0 | ∞ | 0 |
| 6 | 26,55 | 30,05 | ∞ |
Четвертый этап.
Шаг 1. Приведем матрицу расстояний по строкам и столбцам.
| 1 | 3 | 4 | ||
| 2 | ∞ | 0 | 2,42 | 0 |
| 3 | 0 | ∞ | 0 | 0 |
| 6 | 26,55 | 30,05 | ∞ | 26,55 |
↓
| 1 | 3 | 4 | |
| 2 | ∞ | 0 | 2,42 |
| 3 | 0 | ∞ | 0 |
| 6 | 0 | 3,50 | ∞ |
Шаг 2. Определим оценки нулевых клеток:
![]()
Шаг 3. Вычеркиваем клетку с максимальной оценкой. Включаем данную клетку в путь обхода. (3 – 4)
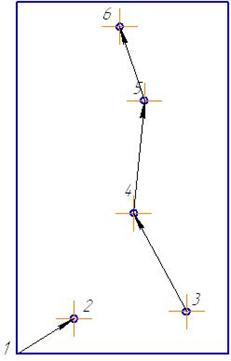
Шаг 4. Переписываем матрицу расстояний, накладывая запрет на одну из клеток для исключения преждевременного замыкания контура (в клетку 6 – 3 ставим ∞).
| 1 | 3 | |
| 2 | ∞ | 0 |
| 6 | 0 | ∞ |
Пятый этап.
Остались не задействованными связи 2 – 3 и 6 – 1.
В результате получаем следующую цепочку:
1→ 2→ 3 → 4→ 5→ 6 →1
Длина пути составляет:
L=18,87+32,06+31,76+32,14+22,14+97,42=234,39
это и есть кратчайший путь.

Похожие работы
... ограничения несовместны, множество планов пусто и задача ЛП решения не имеет. Рис. 1.4 Рис. 1.5 Рис. 1.6 2. Симплекс-метод 2.1 Идея симплекс-метода Рассмотрим универсальный метод решения канонической задачи линейного программирования , , , с n переменными и m ограничениями-равенствами, известный как симплекс-метод. Множество планов канонической задачи – ...
... . 1.3. Построение ограничений и градиента целевой функции : 1.4. Область допустимых решений – отрезок AB. 1.5. Точка А – оптимальная. Координаты т. А: ; ; . 2. Решение задачи линейного программирования симплекс-методом. Прямая задача. Задачу линейного программирования для любой вершины в компактной форме можно представить в виде: Для получения используем алгоритм, приведённый в ...
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...

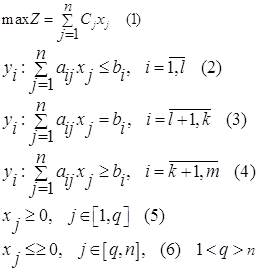


0 комментариев