Решение систем нелинейных алгебраических уравнений методом Ньютона
РЕФЕРАТ
Пояснительная записка: 44 с., 14 рис, 2 таблицы, 3 источника, 4 прил.
Данный продукт представляет собой программу, позволяющую решать СНАУ:
![]() F1(X1, X2, X3)=0,5arctg(X1+X2)+0,2ln(1+X21+ X22+X23)-0,05(X1X2-X1X3-X2X3)+85X1-20X2+35X3-99;
F1(X1, X2, X3)=0,5arctg(X1+X2)+0,2ln(1+X21+ X22+X23)-0,05(X1X2-X1X3-X2X3)+85X1-20X2+35X3-99;
F2(X1, X2, X3)=5arctg(X1+X2+X3)-25,5X1+19,5X2-15,5X3+15;
F3(X1, X2, X3)=-0,3cos(X1-2X2+X3)+0,5exp(-0,25(X21+X22+X23-3))-44,75X1 +20,25X2+5,25X3+18.
Модифицированным методом Ньютона при заданных начальных условиях, где задаётся погрешность вычисления. Кроме вычисления корня уравнения, существует возможность построения графика зависимости приближений двух координат решения. При построении графика задаются промежутки и константы. Программа может использоваться как наглядное пособие для студентов высших учебных заведений.
В программе реализуются:
1) работа с BGI графикой;
2) работа с файлами.
СОДЕРЖАНИЕ
Введение
1. Постановка задачи
1.1. Цель создания программного продукта
1.2. Постановка задачи
2. Математическая модель
3. Описание и обоснование выбора метода решения
4. Обоснование выбора языка программирования
5. Описание программной реализации
1 ПОСТАНОВКА ЗАДАЧИ
1.1 Цель создания программного продукта
Главной целью работы является разработка программы способной решать СНАУ трёх переменных модифицированным методом Ньютона, что должно являться пособием для студентов высших учебных заведений в снижении ненужной нагрузки, связанной с многочисленными массивами вычислений.
1.2 Постановка задачи
В данном программном продукте необходимо реализовать решение СНАУ:
![]() 0,5arctg(X1+X2)+0,2ln(1+X21+ X22+X23)-0,05(X1X2-X1X3-X2X3)+85X1-
0,5arctg(X1+X2)+0,2ln(1+X21+ X22+X23)-0,05(X1X2-X1X3-X2X3)+85X1-
-20X2+35X3-99;
5arctg(X1+X2+X3)-25,5X1+19,5X2-15,5X3+15;
-0,3cos(X1-2X2+X3)+0,5exp(-0,25(X21+X22+X23-3))-44,75X1+20,25X2+
+5,25X3+18.
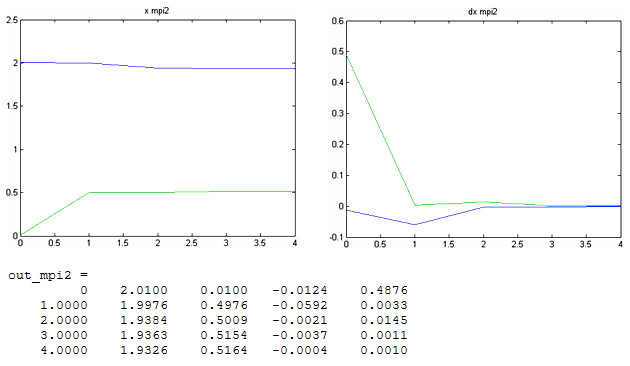
Начальным приближением (X0) должны служить X1,0=0, X2,0=0, X3,0=0. Необходимо ввести точность (ξ) вычисления корня системы уравнений, ограниченную размером (не менее 0,00001). После вычислений с заданной погрешностью возникает множество приближений к корню, последнее из которых будет считаться корнем. После нахождения корня СНАУ и приближений к нему, необходимо построить график зависимости двух любых компонент решения (например, X1 и X3). Для этого третья компонента решения (X3) принимает значение константы. Необходимо указать какая функция будет участвовать в построении графика (например, F1), а также определить промежутки изменения обеих компонент решения (например, [X1min; X1max] и [X3min; X3max]).
2 МАТЕМЕТИЧЕСКАЯ МОДЕЛЬ
Общий вид решения системы нелинейных арифметических уравнений имеет вид:
![]() F1(X1,…,Xn)=0
F1(X1,…,Xn)=0
…
Fn(X1,…,Xn)=0
3 ОПИСАНИЕ И ОБОСНОВАНИЕ ВЫБОРА МЕТОДА РЕШЕНИЯ
Для решения СНАУ был выбран один из численных методов, который называется модифицированным методом Ньютона.
По сравнению с методом Ньютона модифицированный метод Ньютона сходится дольше, но имеет более простой алгоритм реализации, следовательно, проще реализуем программно на языке программирования.
4 ОБОСНОВАНИЕ ВЫБОРА ЯЗЫКА ПРОГРАММИРОВАНИЯ
Реализация поставленной задачи совершается на языке программирования Borland C++ version 3.1.
Система программирования Borland C++, разработанная американской корпорацией Borland, остаётся одной из самых популярных систем программирования в мире. Этому способствует простота лежащая в основе языка программирования C, а также поддержка графического и текстового режимов, что делает Borland C удачным выбором для реализации практически любого программного продукта.
Похожие работы
... 1040, мы все еще получаем сходимость, при количестве итераций порядка 130. 4 Анализ результатов, выводы Целью нашего исследование было сравнение методов простой итерации и Ньютона для решения систем из двух нелинейных уравнений по числу итераций, времени сходимости в зависимости от выбора начального приближения к решению и допустимой ошибки. Зависимость этих параметров от выбора начального ...
... вычисляют в следующем порядке: xjn, xjn–1, …, xj1. 3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений Ax = b с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду x = Bx + c. Здесь B – квадратная матрица с элементами bij (i, ...
... - функции f. Дальше, имеем: . Отсюда , где W'(x) - транспонированная матрица Якоби. Поэтому окончательно , причем . 3. Программная реализация итерационных методов Реализация алгоритмов итерационных методов решения систем нелинейных уравнений будет показана на примере системы: 3.1 Метод простых итераций Приведём систему к виду: Проверим условие ...
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...






0 комментариев