Навигация
Математическая индукция
3.1.1 Математическая индукция
Методом математической индукции называются утверждения вида:
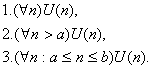
Пусть переменная n имеет область N (натуральные числа). Чтобы доказать первое утверждение, достаточно доказать два утверждения:
![]() (4)
(4)
![]() (5)
(5)
Первое из этих утверждений называется базисом индукции, второе - индукционным шагом. Для доказательства второго утверждения берут произвольное натуральное число, обозначают его какой-либо буквой, скажем k, и доказывают импликацию:
U(k) ® U(k+1) (6)
Как следует из определения квантора общности, доказав это получим (5). Для доказательства (6) предполагают, что истинна посылка:
U(k) (7)
и выводят из этого предположения, что истинно ее заключение U(k+1). Утверждение (7) называется предположением индукции.
При доказательстве утверждения (2) базисом индукции является утверждение U(a), индукционным шагом – ("n³a)(U(n)®U(n+1)), предположением индукции – утверждение U(k), где k – произвольное натуральное число большее или равное a.
При доказательстве утверждения (3) базисом индукции является утверждение U(a), индукционным шагом – утверждение ("n:a£n<b)(U(n)®U(n+1)), предположением индукции U(k), где k – произвольное натуральное число такое, что a£n<b. Такая индукция называется индукцией по интервалу. От индукции по интервалу можно перейти к индукции спуска. Индукцией спуска называется индукция, базисом которой является утверждение U(b), индукционным шагом – утверждение ("n:a£n<b)(U(n+1)®U(n)). Предположением индукции в этой форме является утверждение U(k+1), где k – произвольное натуральное число такое, что a£n<b.
Иногда утверждение 1 удобно доказывать возвратной индукцией. Возвратная индукция - это индукция с базисом U(1), но с индукционным шагом ("n)("m£n)(U(m) ® U(n)). Предположением индукции является ("m<k)U(m), где k – произвольное натуральное число. Возвратная индукция с измененным базисом и индукционным шагом применяется и при доказательстве утверждений 2 и 3.
Для доказательства утверждений 1-3 часто бывает удобной индукция с двойным базисом, то есть для случая 1 индукция с базисом U(1)ÙU(2) и индукционным шагом ("n) ((U(n)ÙU(n+1))®U(n+2)). Иногда удобно применять индукцию с тройным, четырехкратным и т.д. базисом.
Для доказательства утверждений вида
![]() (8)
(8)
применяется индукция по двум переменным. Однако, утверждение (8) часто удается свести к индукции по одной переменной. Для этого формируем в качестве значения переменной m произвольное число и обозначаем его а. Докажем утверждение ("n)U(a,n). Из этого утверждения очевидно следует (8). Но последнее утверждение имеет вид 1 и его можно доказать индукцией. При такой схеме n называется индукционной переменной. Говорят также, что (8) доказывается по n при фиксированном m.
![]()
![]() 3.1.1 Практические задания
3.1.1 Практические задания
1.Требуется найти ошибку в доказательстве того, что натуральные числа равны между собой.
Пусть A переменная с областью определения R(N) (множества натуральных чисел), n – переменная с областью определения N (натуральные числа). Обозначим через U(A, n) высказывание: «Если множество A содержит n элементов, то в A нет двух неравных натуральных чисел». Очевидно, утверждение
![]()
равносильно утверждению задачи.
Докажем утверждение (1) индукцией по n, причем индукцию будем применять в ее простейшей форме. Базисом индукции является:
("A)U(A,1). (2)
Докажем (2). Возьмем произвольное MÌN и докажем
U(M,1). (3)
Тем самым будет доказано утверждение (2). Но на основе определения U, (3) утверждает: «Если множество M содержит один элемент, то в M нет двух неравных натуральных чисел», что очевидно. Предположим теперь в качестве предположения индукции, что ("A)U(A,n) верно для некоторого натурального k, то есть, что верно
("A)U(A,k) (4)
и докажем, что верно
("A)U(A,k+1) (5)
Тем самым утверждение (1) будет доказано. Для доказательства (5) возьмем произвольное MÍN и докажем
U(M,k+1) (6)
Тем самым (5) будет доказано. На основе определения U, (6) есть утверждение: «Если множество M содержит k+1 элементов, то в M нет двух неравных натуральных чисел». Чтобы доказать эту импликацию, предположим, что ее посылка верна. Пронумеруем как-нибудь элементы множества M. Пусть, например:
![]()
Докажем, что в множестве M нет двух неравных натуральных чисел. Тем самым доказательство будет закончено. Рассмотрим два вспомогательных множества:
![]()
Каждое из них получено выбрасыванием из M одного элемента и, следовательно, содержит k элементов. В силу предположения индукции (4) U(K,k) – «Если множество K содержит k элементов, то в K нет двух неравных натуральных чисел». Но множество K как раз содержит k элементов, следовательно, в нем нет двух неравных натуральных чисел. Отсюда:
![]() (7)
(7)
Используем еще раз предположение индукции (4). Возьмем теперь в качестве значения A множество L. Теперь из (4) получим утверждение U(L,k), что означает: «Если множество L содержит k элементов, то в нем нет двух неравных натуральных чисел». Но множество L содержит как раз k элементов, следовательно, в нем нет двух неравных натуральных чисел. В частности:
![]() (8)
(8)
Из (7) и (8) следует, что в M нет двух неравных натуральных чисел. Доказательство закончено.
Похожие работы
... программирование [application programming] — разработка и отладка программ для конечных пользователей, например бухгалтерских, обработки текстов и т. п. Системное программирование [system programming] — разработка средств общего программного обеспечения, в том числе операционных систем, вспомогательных программ, пакетов программ общесистемного назначения, например: автоматизированных систем ...
... разработки программ, но и разработку пакетов прикладных программ. Эти разработки должны обеспечивать высокое качество и вестись примерно так же, как и выпуск промышленной продукции. Достижения компьютерной техники 1. Универсальные настольные ПК Что такое настольный компьютер, объяснять никому не надо — это любимое молодежью устройство, чтобы красиво набирать тексты рефератов, а ...
... набор процедур и функций языков программирования Basic и Pascal, позволяют управлять графическим режимом работы экрана, создавать разнооборазные графические изображения и выводить на экран текстовые надписи. ГЛАВА 2. ГРАФИЧЕСКИЕ ВОЗМОЖНОСТИ ЯЗЫКА ПРОГРАММИРОВАНИЯ В КУРСЕ ИНФОРМАТИКИ БАЗОВОЙ ШКОЛЫ (НА ПРИМЕРЕ BASIC И PASCAL) 2.1 Разработка мультимедиа курса «Графические возможности языков ...
... информационных технологий, которое заключается как в совершенствовании методов организации информационных процессов, так и их реализации с помощью конкретных инструментов – сред и языков программирования. Итогом работы можно считать созданную функциональную модель вычисления неэлементарных функций. Данная модель применима к функциям, если она не задана одной формулой посредством конечного числа ...

0 комментариев