В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара

1.         В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.

2.         На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете. (Решить двумя способами: с помощью 1 и 4 теорем).

3.         Производится бомбометание по трем складам боеприпасов, причем сбрасывается одна бомба. Вероятность попадания в первый склад 0,01; во второй 0,008; в третий 0,025. При попадании в один из складов взрываются все три. Найти вероятность того, что склады будут взорваны.

4.         Круговая мишень состоит из трех зон: I, II, III. Вероятность попадания в первую зону при одном выстреле 0,15, во вторую 0,23, в третью 0,17. найти вероятность промаха.

Занятие №9. Теорема умножения вероятностей.

Перед тем как излагать теорему умножения вероятностей необходимо ввести понятие условной вероятности. Привести учащихся к этому понятию поможет разбор примера.

Пример: Из ящика, в котором 3 белых и 3 черных шаров, наугад вынимают последовательно один за другим два шара. Какова вероятность появления белого шара при втором испытании, если при первом испытании был извлечен черный шар?

Условная вероятность события В при условии, что событие А уже наступило, по определению равна

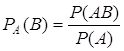 (Р(А)>0).

Опираясь на определение условной вероятности, учащиеся без труда смогут сформулировать теорему о вероятности совместного появления двух событий.

Теорема 1. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предложении, что первое событие уже наступило:

Р(АВ)=Р(А)Р_А(В).

Пусть вероятность события В не зависит от появления события А.

Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, то есть

Р_А(В)=Р(В) или Р_В(А)=Р(А).

Теорема 2. Вероятность совместного появления двух независимых событий равна произведению их вероятностей:

Р(АВ)=Р(А)Р(В).

На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» независимы.

Задачи:

1.         Среди ста лотерейных билетов есть 5 выигрышных. Найти вероятность того, что два наудачу выбранные билета окажутся выигрышными.

2.         В коробке 9 одинаковых радиоламп, 3 из которых были в употреблении. В течение рабочего дня мастеру для ремонта аппаратуры пришлось взять две радиолампы. Какова вероятность того, что обе взятые лампы были в употреблении?

3.         У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков – конусный, а второй – эллиптический?

4.         Бросают два игральных кубика. Какова вероятность того, что на первом кубике выпадет четное число очков, а на втором – число, меньшее 6?

5.         Имеется 3 ящика, содержащих 10 деталей. В первом ящике 8, во втором 7 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.

Занятие №10. Следствия теорем сложения и умножения.

Возвращаясь к занятию №8, где теорема сложения была рассмотрена для несовместных событий, целесообразно изложить теорему сложения для совместных событий. Доказательство приводить не обязательно, надо только ее проиллюстрировать.

Теорема 1. Вероятность появления хотя бы одного из двух совместных событий равна сумме этих событий без вероятности их совместного появления:

k

m

s=mÇk

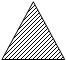
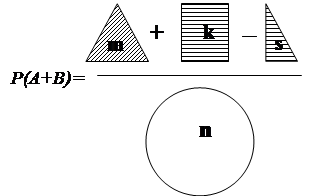Р(А+В)=Р(А)+Р(В)-Р(АВ).

Пусть требуется найти вероятность события А, которое может наступить при условии появления одного из несовместных событий В₁, В₂, …, В_n, образующих полную группу.

Если А произошло вместе с одним из событий В₁, В₂, …, В_n, значит, произошло одно из несовместных событий В₁А, В₂А, …, В_nА.

Таким образом, А= В₁А + В₂А + … + В_nА.

Поскольку события В₁, В₂, …, В_n взаимно несовместны, то и события В₁А, В₂А, …, В_nА обладают тем же свойством. Поэтому

Р(А)= Р(В₁А) + Р(В₂А) + … + Р(В_nА).

По теореме умножения вероятностей зависимых событий имеем ; ; …; .

Поэтому

.

Теорема 2. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В₁, В₂, …, В_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

.

Эту формулу называют «формулой полной вероятности».

С помощью этой формулы находим так называемую формулу Бейеса:

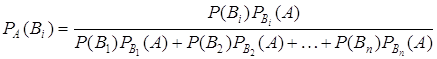 при i=1, 2, …, n.

Особенно широко она применяется при решении задач, связанных с вероятностной оценкой гипотез. Гипотезы – это события, про которых заранее не известно, какое из них наступит.

Доказать формулу Бейеса учащиеся могут самостоятельно.

Задачи:

1.         Подбрасываем две монеты. Какова вероятность выпадения хотя бы одного герба?

2.         Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: р₁=0,7; р₂=0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.

3.         Отдел технического контроля проверяет на стандартность по двум параметрам серию изделий. Было установлено, что у 8 из 25 изделий не выдержан только первый параметр, у 6 изделий – только второй, а у 3 изделий не выдержаны оба параметра. Наудачу берется одно из изделий. Какова вероятность того, что оно не удовлетворяет стандарту?

4.         В лотерее выпущено n билетов, m из которых выигрывают. Гражданин купил k билетов. Какова вероятность того, что один из купленных билетов выигрышный?

5.         В урну, содержащую 2 шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).

6.         Из 10 учеников, которые пришли на экзамен по математике, трое подготовились отлично, четверо – хорошо, двое – удовлетворительно, а один совсем не готовился – понадеялся на то, что все помнит. В билетах 20 вопросов. Отлично подготовившиеся ученики могут ответить на все 20 вопросов, хорошо – на 16 вопросов, удовлетворительно – на 10, и не подготовившиеся – на 5 вопросов. Каждый ученик получает наугад 3 вопроса из 20. Приглашенный первым ученик ответил на все три вопроса. Какова вероятность того, что он отличник?

Занятие №11. Формула Бернулли. Закон больших чисел.

Формула Бернулли намного упрощает путь решения задач в том случае, когда опыты повторяются независимо друг от друга и вероятность интересующего нас события не меняется.

Вероятность того, что при повторных испытаниях событие А наступит m раз и не наступит n-m раз находится по формуле:

.

Вычисления по формуле Бернулли при больших значениях n и m затруднительны. В математике установлены приближенные формулы, позволяющие находить приближенные значения для Р_n(m) и, что еще важнее для практики, суммы значений Р_n(m), таких, что дробь  (относительная частота появления события А) лежит в данных границах.

По формуле Бернулли вероятность того, что в серии из 100 подбрасываний монеты все 100 раз выпадет герб, равна 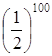, то есть примерно 10^-30. Не столь мала, но все, же ничтожна вероятность того, что цифра выпадет не более 10 раз. Наиболее вероятно, что число выпадений герба будет мало отличаться от 50.

Вообще при большом числе испытаний относительная частота появления события, как правило, мало отличается от вероятности этого события. Математическую формулировку этого качественного утверждения дает принадлежащий Я. Бернулли закон больших чисел, который в уточненной П.Л. Чебышевым гласит:

Теорема. Пусть вероятность события А в испытании s равна р, и пусть проводятся серии, состоящие из n независимых повторений этого испытания. Через m обозначим число испытаний, в которых происходило событие А. Тогда для любого положительного числа e выполняется неравенство

.

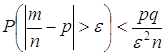Эту теорему лучше давать без доказательства по следующим причинам: во-первых, на доказательство уйдет много времени и, во-вторых, самим доказательством можно «затмить» идею закона больших чисел.

Задачи:

1.         Подбрасываем монету 10 раз. Какова вероятность двукратного появления герба?

2.         Вероятность того, что изделие не пройдет контроля, равна 0,125. какова вероятность того, что среди 12 изделий не будет ни одного забракованного контролером?

3.         вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р=0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.

4.         С разных позиций по мишени выпускают 4 выстрела. Вероятность попадания первым выстрелом примерно 0,1, вторым – 0,2, третьим – 0,3 и четвертым – 0,4. Какова вероятность того, что все четыре выстрела - промахи?

5.         Вы играете в шахматы с равным по силе партнером. Чего следует больше ожидать: трех побед в 4 партиях или пяти побед в 8 партиях?

6.         Сколько раз придется бросать игральную кость, чтобы вероятнейшее число появления шестерки было бы 32?

7.         Какова вероятность равенства с точностью до 0,1 при 100 опытах?

Занятие №13. Самостоятельная работа.

Изучение случайных событий желательно завершить самостоятельной работой, в которой одну-две задачи надо решить как можно большим числом способов. Неплохо включить в работу и теоретический вопрос (чтобы проверить, с одной стороны, понимание учащимися теоретической части пройденного материала и, с другой стороны, умение учащихся формулировать и излагать свои мысли).

Примерный состав самостоятельной работы:

Вариант 1

1.         Среди облигаций займа 25% выигрышных. Найдите вероятность того, что из трех взятых облигаций хотя бы одна выигрышная.

2.         Найти вероятность  по данным вероятностям: Р(А)=а, Р(В)=b, Р(А+В)=с.

3.         Могут ли несовместные события быть в то же время независимыми и наоборот? Привести примеры.

Вариант 2

1.         При включении зажигания двигатель начинает работать с вероятностью р. Найти вероятность того, что для ввода двигателя на работу придется включить зажигание не более двух раз.

2.         Найти вероятность  по данным вероятностям: Р(А)=а, Р(В)=b, Р(А+В)=с.

3.         Почему формула Бернулли применяется при независимости опытов?

Способы решения первых задач подробно изложены в методике.

Занятие №14. Кому нужна теория вероятностей?

Форма организации данного занятия – круглый стол – представление учащимися индивидуальных творческих работ по выбору:

-  небольшая подборка интересных вероятностных задач из различных областей профессиональной деятельности;

-  исследовательская работа в области теории вероятности;

-  индивидуальный проект, отражающий возможность применения знаний по теории вероятности в какой-либо деятельности человека или для какой-либо профессии;

-  написание программ для вычисления вероятностей на каком-либо языке программирования.

Общая тема творческих работ: «Кому нужна теория вероятностей?».

В качестве источников литературы можно порекомендовать следующие книги: Китайгородский, А.И.– посвящена применению законов теории вероятностей к различным жизненным ситуациям и в разных областях науки.

Раздел 3. Случайные величины.

Здесь учащиеся знакомятся еще с одним видом функции – случайной величиной. Эта специфическая числовая функция дополняет и расширяет представление школьников о функциональных зависимостях.

Занятие №1. Понятие случайной величины. Закон распределения вероятностей дискретной случайной величины.

В теории вероятностей приводились события, состоящие в появлении того или иного числа. Например, при бросании игральной кости могли появиться числа 1, 2, 3, 4, 5, 6. Наперед определить число выпавших очков невозможно, поскольку оно зависит от многих случайных причин, которые полностью не могут быть учтены. В этом смысле число очков есть величина случайная; числа 1, 2, 3, 4, 5, 6 есть возможные значения этой величины.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Пример 1. Число родившихся мальчиков среди 100 новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2, …, 100.

Пример 2. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от силы и направления ветра, от температуры и других причин, которые могут полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а, b).

Случайные величины обозначают прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами x, y, z. Например, если случайная величина X имеет три возможных значения, то они будут обозначены так: x₁, x₂,  x₃.

Виды случайных величин

Дискретной или прерывной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины (ДСВ) может быть конечным или бесконечным (см. пример 1).

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений НСВ бесконечно (см. пример 2).

Закон распределения вероятностей ДСВ

На первый взгляд может показаться, что для задания ДСВ достаточно перечислить все ее возможные значения. В действительности это не так: случайные величины могут иметь одинаковые перечни возможных значений, а вероятности их – различные. Поэтому для задания ДСВ не достаточно перечислить всевозможные ее значения, нужно еще указать их вероятности.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения ДСВ первая строка таблицы содержит возможные значения, а вторая – их вероятности:

X	x1	x2	…	xn
p	p1	p2	…	pn

Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что событие X=x₁, X=x₂, …, X=x_n образуют полную группу; следовательно, сумма вероятностей этих событий, то есть сумма вероятностей второй строки таблицы, равна единице: p₁+p₂+…+p_n=1. Если множество возможных значений X бесконечно (счетно), то ряд p₁+p₂+… сходится и его сумма равна единице.

Для наглядности закон распределения ДСВ можно изобразить и графически, для чего в прямоугольной системе координат строят точки (x_i, p_i), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Занятие №2. Математические операции над случайными величинами.

Вначале введем понятие независимости случайных величин.

Две случайные величины называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина. В противном случае случайные величины называются зависимыми. Например, если имеются билеты двух различных денежных лотерей, то случайные величины X и Y, выражающие соответственно выигрыш по каждому билету, будут независимыми, так как при любом выигрыше по билету одной лотереи (например, при X=x_i) закон распределения выигрыша по другому билету (Y) не изменится. Если же случайные величины X и Y выражают выигрыш по билетам одной денежной лотереи, то в этом случае X и Y являются зависимыми, ибо любой выигрыш по одному билету (X=x_i) приводит к изменению вероятности выигрыша по другому билету (Y), то есть к изменению закона распределения Y.

Определим математические операции над ДСВ.

Произведением kX случайной величины Х на постоянную величину k называется случайная величина, которая принимает значения kx_i с теми же вероятностями p_i (i=1, 2, …, n).

m-й степенью случайной величины Х, то есть Х^m, называется случайная величина, которая принимает значение  с теми же вероятностями p_i (i=1, 2, …, n).

Суммой (разностью или произведением) случайных величин Х и Y называется случайная величина, которая принимает все возможные значения вида x_i+y_j (x_i-y_j или x_i∙y_j), где i=1, 2, …, n; j=1, 2, …, m, с вероятностями p_ijтого, что случайная величина Х примет значение x_i, а Y – значение y_j: p_ij=Р[(X=x_i) (Y=y_j)].

Если случайные величины Х и Y независимы, то есть независимы любые события X=x_i, Y=y_j, то по теореме умножения вероятностей для независимых событий

p_ij=Р(X=x_i)∙Р(Y=y_j) = p_i∙p_j.

Занятие №3. Числовые характеристики ДСВ. Математическое ожидание.

Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание.

Для решения многих задач достаточно знать математическое ожидание. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и, следовательно, стреляет лучше второго. Хотя математическое ожидание дает о случайной величине значительно меньше сведений, чем закон ее распределения, но для решения задач, подобных приведенной и многих других, знание математического ожидания оказывается достаточным.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Пусть случайная величина Х может принимать только значения х₁, х₂, …, х_n, вероятности которых соответственно равны р₁, р₂, …, р_n. Тогда математическое ожидание М(Х) случайной величины Х определяется равенством

М(Х)=х₁р₁+х₂р₂+…+х_np_n.

То есть .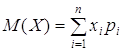

Свойства математического ожидания:

1.         Математическое ожидание постоянной величины равно самой постоянной:

.

2.         Постоянный множитель можно выносить за знак математического ожидания:

.

3.         Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

.

4.         Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:

.

Доказать приведенные свойства учащиеся могут самостоятельно.

Задачи:

Занятие №4. Дисперсия ДСВ.

 

Занятие №5. Среднее квадратическое отклонение.

 

Занятие №6. Метод наименьших квадратов.

 

Занятие №7. Зачет.

Раздел 4. Элементы математической статистики.

В рамках данного элективного курса предполагается познакомить учащихся с элементами статистики как научного направления. Прежде всего речь идет об элементах так называемой «описательной» статистики, которая занимается вопросами сбора и представления первичной статистической информации в табличной и графической формах, вычисления числовых характеристик для совокупности числовых данных.

Включение в курс начальных сведений из статистики направлено на формирование у учащихся таких важных в современном обществе умений, как понимание и интерпретация результатов статистических исследований, широко представленных в средствах массовой информации.

Занятие №1. Выборочный метод.

Статистика – это научное направление, объединяющие принципы и методы работы с числовыми данными, характеризующими массовые явления. Оно включает в себя математическую статистику, общую теорию статистики и целый ряд отраслевых статистик (статистика промышленности, статистика финансов, статистика народонаселения и другие).

Предметом математической статистики является изучение случайных величин по результатам наблюдений. Для получения опытных данных необходимо провести обследование соответствующих объектов. Например, если исследователя интересует вероятность того, что диаметр валика определенного типоразмера после шлифовки окажется за пределами технического допуска, то надо знать закон распределения этого диаметра, а для этого прежде всего нужно располагать набором возможных значений диаметра. Однако обследовать все валики зачастую трудно, поскольку их количество может быть велико. Поэтому приходится из всей совокупности объектов для обследования отбирать только часть, то есть проводить выборочное обследование. В некоторых случаях обследование объектов всей совокупности практически не имеет смысла, поскольку они разрушаются в результате обследования. Таким образом, основным методом статистики является выборочный метод.

Выборочной совокупностью или выборкой называют совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N=1000, а объем выборки n=100.

Для того, чтобы по выборке можно было достаточно уверенно судить о случайной величине, выборка должна быть представительной (репрезентативной). Репрезентативность выборки означает, что объекты выборки достаточно хорошо представляют генеральную совокупность. Заметим, что при отборе объектов могут сыграть роль личные мотивы или психологические факторы, о которых исследователь, проводящий выборку, и не подозревает. При этом, как правило, выборка не будет репрезентативной.

После того как сделана выборка, то есть получена выборочная совокупность объектов, все объекты этой совокупности обследуют по отношению к определенной случайной величине или в результате этого получают наблюдаемые данные.

Задача математической статистики заключается в обработке результатов наблюдений.

Статистическая информация и способы ее представления.

Статистическая информация – это числовые данные о массовых явлениях, это значения наблюдаемых признаков объектов, составляющих статистическую совокупность, которая получена в результате статистического наблюдения. Таким образом, источником статистической информации является реальный опыт, эксперимент, наблюдение, измерение, производимые над реальными объектами и явлениями окружающего мира. Статистика начинается с реальных данных реального опыта; этим она отличается от теории вероятностей, которая изучает математические модели реальных явлений и имеет дело лишь с мысленными (воображаемыми) экспериментами.

Статистика использует методы исследования, основанные на математическом аппарате теории вероятностей, и важнейшим среди этих методов является выборочный метод. Поэтому математическая статистика и теория вероятностей неразрывно связаны между собой, постоянно взаимодействуют, и между ними не существует четкой и общепризнанной границы.

Статистическая информация о результатах наблюдений или экспериментов может быть зарегистрирована и представлена в различных формах.

1)         Простой статистический ряд, или ряд данных, или выборка: х₁, х₂, х₃, …, х_n-1, х_n – запись результатов в порядке их появления (или получения), запись в ряд. Отдельные значения х_i, составляющие этот ряд, называют вариантами или просто данными, или результатами наблюдений. Количество вариант в ряду n называют объемом ряда, или объемом выборки.

Например, игральный кубик бросили 12 раз и записали выпавшие числа в порядке их появления: 3, 4, 5, 6, 6, 6, 5, 1, 4, 6, 1, 4 (п=12).

Недостатки: громоздкость и труднообозримость.

2)         Вариационный ряд, или упорядоченный.

1, 1, 3, 4, 4, 4, 5, 5, 6, 6, 6, 6.

Недостаток: громоздкость.

3)         Статистическое распределение ряда:

xj	1	3	4	5	6
nj	2	1	3	2	4

Величины n_j называются частотами значений варианты х_j. Значение варианты х_j и варианты х_i – это не одно и то же: каждое значение фиксируется только один раз, а варианты с таким значением могут встречаться в ряду многократно. (j=1, 2, 3, 4, 5 ; i=1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12). j=1, 2, …, m, а i=1, 2, …, n, причем всегда m£n (если m=n, то все варианты в ряду разные).

Наряду с частотами используются относительные частоты .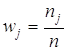

4)         Интервальный ряд: весь диапазон наблюдаемых значений признака х_max-x_minразбивают на небольшое число (k=6 … 10) частичных интервалов, и подсчитывают количество вариант исходного ряда, попадающих в каждый частичный интервал.

5)         Графическая форма: столбчатая диаграмма, полигон частот, гистограмма, круговая диаграмма.

Задачи:

1.         Рост каждого из 50 одиннадцатиклассников занесли в таблицу:

165	170	165	165	175	160	170	170	172	170
178	170	178	174	165	165	175	175	172	160
175	172	160	170	170	178	176	176	175	172
170	170	172	170	178	176	180	174	176	181
180	170	170	174	180	175	175	174	174	172

По имеющимся данным составить таблицу распределения значений случайной величины Х – роста одиннадцатиклассников: а) по частотам (М); б) по относительным частотам (W).

2.         После группировки данных эксперимента получилась такая таблица их распределения:

Варианта	-3	0	4	5	9	11	12	15	20
Кратность варианты	12	9	1	64	34	56	7	8	9

а)         Определите объем выборки.

б)         Найдите наиболее часто встретившуюся варианту.

в)         Допишите к таблице третью и четвертую строки из частот и процентных частот вариант.

г)         Найдите сумму чисел в третьей и четвертой строках.

Сделайте выводы.

Могут быть использованы следующие задачи: С10, С14, С23, С25, С34, С36, С42, С49

Занятие №2. Числовые характеристики статистических рядов.

Сбор и анализ статистических данных не является самоцелью; результаты статистических исследований позволяют принимать более правильные управленческие решения, выявлять закономерности и взаимозависимости, скрытые за случайными колебаниями, ошибками и искажениями.

Нередко возникает необходимость сравнить между собой две или несколько совокупностей статистических данных. Поскольку сравнение производится по какому-то определенному свойству, то для проведения сравнения нужны показатели, характеризующие то или иное свойство в совокупности данных одним числом. Такие показатели в статистике получили наименование числовых характеристик (статистических характеристик).

Простейшими числовыми характеристиками являются характеристики положения (среднее значение, мода, медиана) и характеристики рассеивания (размах, выборочная дисперсия, выборочное среднее квадратичное отклонение).

Среднее значение ряда наблюдений  - это центр рассеивания наблюдаемых значений, это расчетное значение, сумма отклонений всех вариант от которого равна нулю.

Если варианты в ряду х_i являются значениями непосредственно наблюдаемого признака, то среднее значение ряда  находят по формуле среднего арифметического:

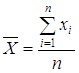 (формула простой средней),

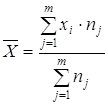 (формула средней взвешенной).

В статистике при вычислении средних ставится задача заменить все индивидуальные наблюдаемые значения признака некоторой обобщающей уравненной величиной  так, чтобы при этом не изменялась некоторая итоговая величина для всей совокупности. Этой величиной может быть сумма всех вариант (среднее арифметическое) или их произведение (среднее геометрическое), или сумма обратных величин (среднее гармоническое), или сумма квадратов вариант (среднее квадратичное) и так далее. Общая формула степенной средней:

,

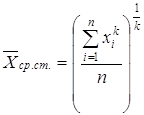при k=-1 получаем среднюю гармоническую, при k=1 – среднюю арифметическую, при k=2 – среднюю квадратичную, и так далее. Отдельно вводится понятие среднего геометрического

.

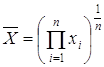Правило мажорантности средних: _гарм£_геом£_арифм£_квадр.

Выбор формулы для вычисления среднего определяется решаемой задачей.

Следующей числовой характеристикой статистических рядов является мода. Мода Мо – это значение вариант, встречающееся в ряду чаще других. В таблице распределения ряда мода – это значение х_j, которому соответствует наибольшее значение частоты n_j. Статистический ряд может иметь одну, две или несколько мод, может не иметь моды.

Медиана Ме – это срединная в вариационном ряду значение варианты. Если число членов ряда n нечетное, то

, где  - целая часть числа .

Если n четное, то .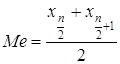

Простейшей характеристикой рассеивания является размах: А=х_max-x_min; размах есть разность между наибольшим и наименьшим значениями вариант в ряду.

Выборочная дисперсия D_выб(Х) есть среднее значение квадратов отклонений всех вариант от среднего значения ряда :

.

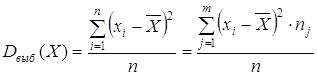Для практических расчетов удобнее формула:

.

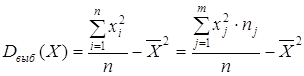Дисперсия имеет размерность квадрата наблюдаемой величины, поэтому на практике широко используется еще один показатель рассеивания – среднее квадратичное отклонение s_выб(Х):

.

Важно помнить о принципиальном отличии числовых характеристик в статистике от числовых характеристик в теории вероятностей.

Задачи:

С62, С69, С87, С 93 С95 из пособия.

Занятие №3. Статистические исследования. Этапы статистического исследования.

Для изучения различных общественных и социально-экономических явлений, а также некоторых процессов, происходящих в природе, проводят специальные статистические исследования.

Всякое статистическое исследование начинается с целенаправленного сбора информации об изучаемом явлении или процессе. Этот этап называется этапом статистического наблюдения.

Для обобщения и систематизации данных, полученных в результате статистического наблюдения, их по какому-либо признаку разбивают на группы, и результаты группировки сводят в таблицы (таблицы частот, таблицы относительных частот). Таким образом, второй этап – группировка и сведение данных в таблицу.

Данные нужно представить более наглядно: либо с помощью столбчатой диаграммы, либо полигона частот, либо круговой диаграммы, либо гистограммы. Третий этап – наглядное представление данных.

Далее переходят к анализу данных, используя для этого различные обобщающие показатели (статистические характеристики: среднее значение, мода, медиана, размах, выборочная дисперсия, выборочное среднее квадратичное отклонение).

На основании цели проведения статистического исследования и анализа данных делается вывод.

Рассмотрим такой пример. Администрация школы решила проверить математическую подготовку одиннадцатиклассников. С этой целью был составлен тест, содержащий 6 заданий. Сделали выборочное обследование, выбрали 20 школьников, случайный отбор обеспечивает одинаковую вероятность попадания в выборку любого объекта генеральной совокупности. Получили следующие результаты такого выборочного обследования:

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
4	2	0	6	2	3	4	3	3	0	1	5	2	6	4	3	3	2	3	1

На основании этого ряда трудно сделать какие-либо определённые выводы о том, как справились школьники с работой. Чтобы удобней было анализировать информацию, в подобных случаях данные ранжируют, располагая их в порядке возрастания. Ряд примет вид:

0011222233333344456

Каждая группа представляет определённый результат эксперимента:

·          Не решено ни одной задачи;

·          Решена 1 задача;

·          Решены 2 задачи и так далее.

В нашем случае частота появления события «0 задач» – 2, относительная частота 2/20=10%. Собственная частота появления события «2 задачи» – 4, относительная частота 4/50=8% и так далее.

Составим таблицу:

Событие	0	1	2	3	4	5	6
Частота	2	4	4	6	3	1	1
%	10	8	8	14	6	2	2

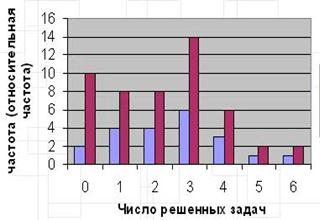
С помощью ранжирования ряда, таблицы и графических иллюстраций, мы уже получили первоначальные сведения о закономерностях интересующего нас ряда данных. Если нужно знать наиболее типичный результат, то используют понятия медиана, мода, размах, выборочная дисперсия, выборочное среднее квадратичное отклонение.

Задание: Провести какое-либо статистическое исследование.

Занятие №4. Определение линий регрессии методом наименьших квадратов для двумерных выборок.

Занятие №5.

Заключение

Настоящее исследование посвящено решению актуальной проблемы теории и методики обучения математике – развитие пространственного мышления учащихся в процессе изучения геометрии. Основным средством для решения этой проблем был выбран компьютер, который позволил выделить новый вид учебной наглядности – компьютерная анимация, реализующаяся посредством пакета прикладных программ 3D Studio MAX.

В соответствии с поставленными целями перед данной выпускной квалификационной работой и результатами, полученными в ходе исследования, можно сделать следующие выводы:

Анализ научно-методической литературы, посвященной вопросам формирования и развития пространственных представлений, позволил выделить основные психические и физиологические основы восприятия человеком объектов окружающего мира. В результате была выработана общая схема восприятия, которая легла в основу разработанной методики формирования пространственных представлений.

Была выявлена возможность применения компьютерной анимации в процессе формирования пространственных представлений. Компьютерная анимация заполнила некоторый пробел в процессе формирования пространственного образа геометрического объекта, она позволила осуществить плавный переход от натуральной вещественной модели к условно-графическому изображению – чертежу, что в значительной степени повышает уровень объективности пространственных представлений обучаемого.

Была разработана соответствующая методика формирования пространственного образа геометрического объекта при помощи компьютерной анимации. По результатам опытной работы можно сделать вывод о положительном влиянии разработанной методики на формирование пространственных представлений учащихся. Систематизация результатов научно-методических исследований позволила выявить условия формирования пространственных представлений обучаемых: использование различных видов деятельности, в первую очередь деятельности по решению специально подобранных упражнений, ориентированных на развитие пространственных представлений обучаемых; взаимосвязь формирования пространственных представлений с развитием логического мышления и речи учащихся; использование рациональной системы средств наглядности. Как показала практика преподавания, учет и использование этих условий и приемов успешно способствует работе по развитию пространственных представлений обучаемых. Опытная работа по применению разработанной методики показала ее эффективность. Опытная работа доказала, что целенаправленное и рациональное внедрение в практику новой учебной наглядности - компьютерной анимации ведет к повышению уровня развития пространственных представлений учащихся.

Сделанные выводы дают основание полагать, что справедливость гипотезы исследования экспериментально подтверждена, все поставленные задачи исследования решены.

Библиографический список

Сборники нормативных документов

 

1.         Сборник нормативных документов. Математика [Текст] / сост. Э.Д.Днепров, А.Г. Аркадьев. – М.: Дрофа, 2006. – 80 с.

2.         Концепция развития школьного математического образования [Текст] // Математика в школе. – 1990. – № 1. – С. 2 – 14.

3.         Стандарт.

Учебники для вузов и техникумов с этими разделами

4.         Кремер, Н.Ш. Теория вероятностей и математическая статистика [Текст]: учебник для вузов / Н.Ш. Кремер. – М.: ЮНИТИ-ДАНА, 2002. – 543 с.

5.         Курс высшей математики для гуманитарных специальностей [Текст]: учебное пособие / под ред. Ю.Д.Максимова. – СПб.: Специальная литература, 1999. – 191 с.

6.         Воронов,М.В. Математика для студентов гуманитарных факультетов [Текст] / М.В. Воронов, Г.П. Мещерякова. – Ростов-на-Дону: Феникс, 2002. – 384 с.

7.         Солодовников, А.С. Теория вероятностей [Текст] / А.С. Солодовников. – М.: Просвещение, 1978. – 192 с.

8.         Баврин, И.И. Курс высшей математики [Текст] / И.И. Баврин. – М.: Просвещение, 1992. – 400 с.

9.         Гмурман, В. Е. Теория вероятностей и математическая статистика [Текст]: учебное пособие / В.Е. Гмурман. – М.: Высшее образование, 2006. – 479 с.

10.      Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике [Текст]: учебное пособие / В. Е. Гмурман. – М.: Высшая школа, 1999. – 400 с.

11.      Вентцель, Е.С. Теория вероятностей [Текст] / Е.С. Вентцель. – М.: Высшая школа, 2001. – 575 с.

12.      Калинина, В. Н. Математическая статистика [Текст]: учебник для студ. сред. спец. учеб. заведений / В.Н. Калинина, В.Ф. Панкин. – М.: Дрофа, 2002. – 336 с.

Научная и научно-популярная литература

13.      Виленкин Н. Я. Комбинаторика [Текст] / Н. Я. Виленкин А.Н. Виленкин, П.А. Виленкин. – М.: ФИМА, МЦНМО, 2006. – 400 с.

14.      Китайгородский, А.И. Невероятно – не факт [Текст] / А.И.Китайгородский. – М.: Молодая гвардия, 1972. – 256 с.

15.      Хургин, Я.И. Как объять необъятное [Текст] / Я.И. Хургин. – М.: Знание, 1992. – 192 с.

16.      Виленкин, Н. Я. Популярная комбинаторика [Текст] / Н.Я. Виленкин. – М.: Наука, 1975. – 208 с.

Методическая литература и пособия для учащихся

17.      Глеман, М. Вероятность в играх и развлечениях. Элементы теории вероятностей в курсе сред. школы [Текст]: пособие для учителя / М. Глеман, Т. Варга; пер. с фр. – М.: Просвещение, 1979. – 176 с.

18.      Шихова, А. П. Обучение комбинаторике и ее приложениям в средней школе [Текст] / А. П. Шихова. – Киров: ИУУ, 1994 – 63 с.

19.      Афанасьев, В.В. Школьникам о вероятности в играх. Введение в теорию вероятностей для учащихся 8-11 классов [Текст] / В.В.Афанасьев, М.А.Суворова. – Ярославль: Академия развития, 2006. – 192 с.

20.      Предпрофильная подготовка учащихся 9 классов по математике. Общие положения, структура портфолио, программы курсов, сценарии занятий [Текст] / И.Н.Данкова, Т.Е.Бондаренко, Л.Л. Емелина, О.К. Плетнева. – М.: 5 за знания, 2006. – 128 с.

21.      Бунимович, Е.А. Вероятность и статистика. 5-9 кл. [Текст]: пособие для общеобразоват. учеб. заведений / Е.А. Бунимович, В.А. Булычев. – М.: Дрофа, 2002. – 160 с.

22.      Сборник задач по математике для факультативных занятий в 9-10 классах [Текст] / под ред. З. А. Скопеца. – М.: Просвещение, 1971. – 208 с.