Граф-дерево (называют за внешнее сходство с деревом)

1.         Граф-дерево (называют за внешнее сходство с деревом).

С помощью дерева проиллюстрируем проведенный перебор вариантов в примере 1.

На первом месте в трехзначном числе может стоять одна из цифр 1, 2 или 3; на втором и третьем местах – (при условии, что цифры могут повторяться) также любая из трех цифр.

Таким образом, с помощью графа-дерева подсчет вариантов гораздо легче производить. Также вычерчивать дерево вариантов полезно, когда требуется записать все существующие комбинации элементов.

2.         Полный граф. Используется для решения задач, в которых все элементы множества взаимосвязаны.

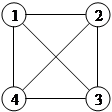Пример 2. При встрече каждый из друзей пожал другому руку (каждый пожал каждому). Сколько рукопожатий было сделано, если друзей было четверо?

Четырех друзей поместим в вершины графа и проведем все возможные ребра. В данном случае отрезки-ребра обозначают рукопожатия каждой пары друзей.

Из рисунка видно, что граф имеет 6 ребер, значит, и рукопожатий было сделано 6.

Еще одним методом подсчета числа комбинаций является таблица вариантов. Ее можно использовать, когда составляемые комбинации состоят из двух элементов.

Пример 3. Записать всевозможные двузначные числа, используя при этом цифры 0, 1, 2 и 3. Подсчитать их количество N.

Для подсчета образующих чисел составим таблицу:

1-я цифра	2-я цифра
	0	1	2	3
1	10	11	12	13
2	20	21	22	23
3	30	31	32	33

N=3·4=12

Задачи:

1.         По окончании деловой встречи специалисты обменялись визитными карточками (каждый вручил свою карточку каждому). Сколько всего визитных карточек было роздано, если во встрече участвовало 5 человек?

2.         Перечислить все возможные цветовые сочетания брюк, свитера и ботинок, если в гардеробе имеются брюки трех цветов: серые, бежевые и зеленые; свитера двух расцветок: песочный и малиновый; ботинки двух цветов: черные и коричневые.

3.         Одновременно происходят выборы мэра города и префекта округа. На должность мэра выставили свои кандидатуры Алкин, Балкин, Валкин, а на должность префекта – Эшкин, Юшкин, Яшкин.

а)            Нарисуйте дерево возможных вариантов голосования и определите с его помощью число различных исходов.

б)            В скольких вариантах будет кандидатура Эшкина?

в)            В скольких вариантах фамилии кандидатов на должность мэра и на должность префекта состоят из разного числа букв?

г)             Как изменятся ответы в пунктах а) и б), если учесть еще кандидата «против всех»?

4.         Группа туристов планирует осуществить поход по маршруту Антоново – Борисово – Власово - Грибово. Из Антонова в Борисово можно сплавиться по реке или дойти пешком. Из Борисова во Власово можно дойти пешком или доехать на велосипедах. Из Власова в Грибово можно доплыть по реке, доехать на велосипедах или дойти пешком.

а)         Нарисуйте дерево возможных вариантов похода.

б)         Сколько всего вариантов похода могут выбрать туристы?

в)         Сколько есть полностью не пеших вариантов?

г)         Сколько вариантов похода могут выбрать туристы при условии, что хотя бы на одну из участков маршрута они должны использовать велосипеды?

5.         С помощью таблицы вариантов перечислить все возможные двухбуквенные коды (буквы в коде могут повторяться), в которых используются буквы а, б, в.

6.         Составляя расписание уроков на понедельник для 10А класса, завуч хочет первым уроком поставить либо физику, либо алгебру, а вторым – либо русский язык, либо литературу, либо историю. Сколько существует вариантов составления расписания на первые два урока?

Определиться в успешности усвоения данной темы поможет самостоятельное составление учащимися задач. Можно предложить им придумать так называемое «задание для друга» с использованием каждого из трех методов.

Занятие №3. Кортежи. Правило произведения.

Второй этап формирования вычислительных навыков в решении комбинаторных задач связан с формированием правил суммы и произведения. Предлагаемая методика формирования правил суммы и произведения и последующих основных комбинаторных понятий базируется на таких теоретико-множественных понятиях, как множество, элемент множества, подмножество, упорядоченное множество. Поэтому с учащимися необходимо повторить эти понятия.

Рассмотрим задачу про «Суеверного председателя».

«Опять восьмерка!» - горестно воскликнул председатель клуба велосипедистов, взглянув на прогнутое колесо своего велосипеда. «А все почему? Да потому, что у меня членский билет № 888 – целых три восьмерки. И теперь не проходит и месяца, чтобы то на одном, то на другом колесе не появилась восьмерка. Надо менять номер билета! А чтобы меня не обвинили в суеверии, проведу ка я перерегистрацию всех членов клуба и буду выдавать только билеты с номерами, в которые не входит ни одна восьмерка. Не знаю только, хватит ли на всех номеров – ведь у нас в клубе почти 600 членов. Неужели придется сначала выписать все номера от 000 до 999, а затем вычеркивать из них все номера с восьмерками?» Чтобы помочь председателю, нам нужно решить такую комбинаторную задачу (учащимся можно предложить ее сформулировать):

Сколько существует трехзначных номеров, не содержащих цифры 8?

Далее учащиеся должны ответить на вопросы (Как бы вы решили такую задачу? С помощью какого метода? Какие еще методы решения применимы к данной задаче?) и вместе с учителем разобрать решение данной задачи.

Сначала найдем количество однозначных номеров, отличных от 8. Ясно, что таких номеров девять: 0,1,2,3,4,5,6,7,9. А теперь найдем все двузначные номера, не содержащие восьмерок. Их можно составить так: взять любой из найденных однозначных номеров и написать после него любую из девяти допустимых цифр. В результате из каждого однозначного номера получится 9 двузначных. А так как двузначных номеров было 9, то получится 9·9 = 9² двузначных номеров.

Итак, существует 9² = 81 двузначный номер без цифры 8. Но к каждому из этих номеров можно приписать справа любую из цифр 0,1,2,3,4,5,6,7,9 и получить трехзначный номер, не содержащий цифру 8. При этом получаются все трехзначные номера с требуемым свойством. В результате мы нашли 9²·9 = 9³ = 729 трехзначных номеров без восьмерок.

Если бы председатель клуба был еще суевернее и отказался и от цифры 0, поскольку она походит на вытянутое колесо, то он смог бы составить лишь 8³ = 512 трехзначных номеров и их уже не хватило бы на всех членов клуба.

С помощью этого примера вводятся понятие кортежа и правило произведения.

Кортежи. Номера, составленные из трех цифр, нельзя рассматривать как множество элементов. Во-первых, в номерах цифры могут повторяться (например, 775), а в множествах элементы не повторяются, во-вторых, в номерах важен порядок цифр (175 и 571 – совсем разные номера), а в множествах порядок элементов роли не играет. Поэтому, если мы хотим изучать такие объекты, как номера, или слова (в них тоже могут буквы повторяться, от перестановки букв слово меняется), нужно ввести новое математическое понятие, отличное от понятия множество.

Это новое понятие математики назвали кортежем (наряду со словом «кортеж» применяют названия «слово», «набор», «вектор», «конечная последовательность» и т.д.). Кортеж – французское слово, означающее торжественное шествие. И у нас иногда говорят «кортеж автомашин», «свадебный кортеж» и т.д. При этом кортеж автомашин может состоять из нескольких «Волг», нескольких «БМВ» и нескольких «Ауди». Если считать машины одной и той же марки неразличимыми, то получим, что в кортеже автомашин один и тот же элемент может повторяться несколько раз.

В математике кортеж определяют так. Пусть имеется несколько множеств X₁, …, X_k. Представим себе, что их элементы сложены в мешки, а мешки перенумерованы. Вытащим из первого мешка какой-нибудь элемент (то есть возьмем какой-нибудь элемент а₁ множества Х₁), затем вытащим элемент а₂ из мешка Х₂ и будем продолжать этот процесс до тек пор, пока из мешка Х_k не будет вытащен элемент а_k. После этого расставим полученные элементы в том порядке, в котором они появились из мешков (а₁, а₂, …, а_k). Это и будет кортежем длины k, составленным из элементов множеств X₁, …, X_k. Элементы а₁, а₂, …, а_k называют компонентами кортежа.

Два кортежа называют равными в том и только в том случае, когда они имеют одинаковую длину, а на соответствующих местах стоят одни и те же элементы.

Здесь учащимся можно дать индивидуальное задание: взять любое множество и составить из его элементов кортеж, при этом спросить их, почему он является кортежем, и сколько кортежей можно составить из этого множества?

При больших значениях n (n – это количество элементов в множестве, из которого составляется кортеж) и k (k – это количество элементов в кортеже) перебор вариантов становиться очень громоздким, поэтому ограничиваются только подсчетом общего числа возможных вариантов построения кортежей. Для простейших комбинаторных задач формулы для подсчета числа возможных кортежей получаются с помощью двух основных правил комбинаторики.

Правило суммы. Если элемент а можно выбрать m способами, а элемент b можно выбрать n способами, причем любой выбор элемента a отличен от любого выбора элемента b, то выбор «a или b» можно сделать m + n способами. (Например, если на блюде лежат 7 яблок и 4 груши, то выбрать один плод можно 7+4=11 способами).

На языке теории множеств это правило формулируется следующим образом: Если пересечение конечных множеств A и B пусто, A∩B=Ø, то число элементов в их объединении равно сумме чисел элементов множеств A и B: A∩B=Ø =>

Здесь целесообразно задать учащимся вопросы: А как будет сформулировано правило суммы для пересекающихся множеств A и B? в общем случае для конечного числа множеств?

Правило суммы применяется для решения комбинаторных задач. Именно, часто приходится разбивать все множество перечисляемых комбинаций, подсчитывать число элементов в каждой группе и потом складывать получившиеся ответы.

Правило произведения. Возьмем несколько конечных множеств X₁, …, X_k, состоящих соответственно из n₁, …, n_k элементов, и найдем, сколько кортежей длины k можно составить из элементов этих множеств. Способ, которым мы решим эту задачу по сути дела будет тем же самым, каким было найдено число трехзначных номеров без восьмерок. Сначала найдем число кортежей длины 1, составленных из элементов множества Х_1. Ясно_, что их число равно n₁. Возьмем теперь один из этих кортежей (а₁) и припишем к элементу а₁ справа по очереди все элементы множества х₂.Получится n₂ кортежей длины 2, у которых первая координата равна а₁. Но вместо а₁ можно было бы взять любой другой элемент из Х₁. Поэтому получается n₁ раз по n₂ кортежа, а всего n₁∙ n₂ кортежей длины 2 или, как чаще говорят пар. Из каждой такой пары получим n₃ троек, приписав к ней по очереди все элементы множества Х₃, а всего n₁∙ n₂∙ n₃ троек. Продолжая этот процесс, получим, в конце-то концов, n₁∙ n₂∙ …∙ n_k кортежей длины k, составленных из элементов наших множеств.

Полученный результат является одним из важнейших в комбинаторике. На нем основан вывод многих формул комбинаторики. Его называют «правилом произведения». Сформулируем это правило так. Если элемент а₁ можно выбрать n₁ способами, после каждого выбора этого элемента следующий за ним элемент а₂ можно выбрать n₂ способами … после выбора элементов а₁, а₂, …, а_k-1 элемент а_k выбирается n_k способами, то кортеж (а₁, а₂, …, а_k) можно выбрать n₁ ∙ n₂ ∙ … ∙ n_k.

Подсчитаем, например, сколько слов, содержащих 6 букв, можно составить из 33 букв русского алфавита при условии, что любые две стоящие рядом буквы различны (например, слово «корова» допускается, а слово «колосс» нет). При этом, разумеется можно писать бессмысленные слова. В этом случае на первое место у нас 33 кандидата. Но после того, как первая буква выбрана, вторую можно выбрать лишь 32 способами – ведь повторять первую букву нельзя. На третье место тоже 32 кандидата – первую букву уже можно повторить, а вторую – нельзя. Также убеждаемся, что на все места, кроме первого, имеется 32 кандидата. А так как число этих мест равно 5, то получаем ответ 33∙32∙32∙32∙32∙32=1107396236.

Задачи на непосредственное применение комбинаторных правил произведения и суммы:

1.         В отделе научно-исследовательского института работают несколько человек, причем каждый из них знает хотя бы один иностранный язык, 6 человек знают английский, 6 – немецкий, 7 – французский, 4 знают английский и немецкий, 3 – немецкий и французский, 2 – французский и английский, 1 человек знает все три языка. Сколько человек работает в отделе? Сколько из них знают только английский язык? Сколько человек знают только один язык?

2.         Сколько чисел среди первых 100 натуральных чисел не делятся ни на 2, ни на 3, ни на 5?

3.         Имеется 5 видов конвертов и 4 вида марок. Сколькими способами можно выбрать конверт и марку для посылки письма?

4.         Сколькими способами можно выбрать на шахматной доске черный и белый квадраты, не лежащие на одной горизонтали или одной вертикали?

5.         Имеется 20 тетрадей в линейку и 30 тетрадей в клетку. Необходимо выбрать две тетради одного вида. Сколько способов выбора двух тетрадей возможно, если учитывается порядок выбора тетрадей?

Занятия №4, 5, 6. Размещения. Перестановки. Сочетания.

Эти занятия можно построить с использованием презентации (см. Приложение 1) по единой схеме: определение → вывод формулы (доказательство) → пример. По мере рассмотрения каждого из комбинаторных понятий целесообразно отработать с учащимися эти понятия на символическом материале. Для усвоения содержания понятия нужно рассмотреть упражнения по составлению объектов, относящихся к определенному комбинаторному понятию. Эти упражнения должны носить внутримодельный характер. Упражнения лучше давать на карточках. Систему упражнений и задач можно подобрать из.

Занятие №7. Самостоятельная работа.

В начале занятия учащиеся должны самостоятельно заполнить таблицу, представленную в презентации (слайд 23), что будет способствовать систематизации и актуализации знаний, полученных на предыдущем занятии.

Вариант 1

1.         Сколькими способами можно обозначить вершины данного треугольника, используя буквы A, B, C, D, E и F?

2.         Курьер должен разнести пакеты в 7 различных учреждений. Сколько маршрутов может он выбрать?

3.         Сколькими способами можно разделить 6 различных конфет между тремя друзьями?

4.         Сколько различных маршрутов может избрать пешеход, решив пройти 9 кварталов, из них 5 на запад и 4 на юг?

5.         В магазине продают кепки трёх цветов: белые, красные и синие. Наташа и Лена покупают себе по одной кепке. Сколько существует различных вариантов покупок для этих девочек?

6.         Каждая из 5 подруг собирается вечером пойти либо в кино, либо на каток. Сколькими различными способами эти пять подруг смогли бы провести вечер?

Вариант 2

1.         Сколькими способами можно обозначить вершины куба буквами A, B, C, D, E, F, G, K?

2.         Сколькими способами можно разложить 12 различных деталей по трем ящикам?

3.         Сколькими способами могут быть распределены первая, вторая и третья премии между 13 участниками конкурса?

4.         В библиотеке Кате предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими способами она может выбрать из них 3 книги и 2 журнала?

5.         Найти число различных способов, которыми можно записать в один ряд 6 плюсов и 4 минуса.

6.         В списке класса для изучения английского языка 15 человек. Сколько существует вариантов присутствия (отсутствия) этих людей на занятии?

Занятие №8. Некоторые свойства сочетаний.

Этот вопрос можно предложить учащимся в качестве самостоятельной работы.

I.

а) Составьте всевозможные сочетания по 2 элемента без повторений из элементов множества М={а, б, в, г, д}. Для каждого из составленных подмножеств выпишите дополнения - трехэлементные подмножества оставшихся элементов - и сравните число тех и других. Какой вывод можно сделать о числах и ?

б)Из n элементов некоторого множества составлены всевозможные k-элементные подмножества и соответствующие им дополнения — (n-k) – элементные подмножества оставшихся элементов. Какой вывод можно сделать о сравнительной величине чисел  и ?

в) Воспользуйтесь формулой подсчета числа сочетаний без повторений и докажите равенство =. Это равенство выражает одно из важных свойств сочетаний. Им удобно пользоваться для вычисления  в случае k>n.

г) Не производя вычислений, выберите равные из следующих чисел: , , , , , , , , , , , , , .

д) Вычислите , , .

е) Множество М={а, б, в, г, д, е} разбейте всеми возможными способами на два подмножества так, чтобы в одно из них входило 2 элемента, а в другое - 4.

ж) Из 12 человек нужно составить 2 волейбольные команды по 6 человек в каждой. Сколькими способами это может быть сделано?

II. Докажите следующее свойство сочетаний:

+++…+=2ⁿ.

а) Возьмите множество М={а, b, с} из трех элементов и составьте k-элементные подмножества М /k=0, 1, 2, 3/.

Каждому подмножеству поставьте в соответствие последовательность из трех цифр – единиц и нулей – следующим образом: каждому из трех элементов а, b, с поставьте в соответствие 1, если он входит в подмножество, 0 – если он в подмножество не входит. Рассмотрите таблицу

Таблица 1.

Виды подмножеств	Число подмнож.	Подмножества	Последовательности из 1 и 0
Пустые		Æ	000
Одноэлементные		{a}, {b}, {c}	100, 010 ,001
Двухэлементные		{ab}, {ac}, {bc}	110, 101 ,011
Трехэлементные		{a, b, c}|	111

Число всех подмножеств множества М равно +++ и равно числу всех последовательностей длины три из единиц и нулей. Число таких последовательностей нетрудно подсчитать: каждое из трех мест в последовательности может быть занято 1 или 0, то есть двумя способами, а все три места – по принципу умножения – 2×2×2=2³ способами. Это число можно получить и по формуле подсчета числа размещений с повторением, таким образом, +++=2³.

б) Проведите аналогичные рассуждения для множества из n элементов. Тогда какие изменения следует внести в таблицу? Сделайте вывод, результат запишите.

Занятие №9. Свойство сочетаний =+ и треугольник Паскаля.

I. Для изучения следующего свойства сочетаний предварительно составим трехэлементные подмножества множества М={а, б, в, г, д}. Затем выберем из множества М любой элемент, например, «а» и разобьем все подмножества на два класса: не содержащие «а» и содержащие «а».

I класс: {б, в, г}, {б, в, д}, {б, г, д}, {в, г, д}

II класс: {а, б, в}, {а, б, г}, {а, б, д}, {а, в, г},

{а, в, д}, {а, г, д}.

Первый класс состоит из всевозможных сочетаний без повторений по три элемента из следующих четырех: б, в, г, д. Таких сочетаний . Каждое подмножество второго класса состоит из элемента «а» и двух элементов, выбираемых из множества следующих элементов: б, в, г, д. Очевидно, число таких подмножеств равно .

Подмножества I и II классов исчерпывают все трехэлементные подмножества множества М, что означает:

=+.

Аналогичными рассуждениями получите равенство:

=+.

Убедитесь в справедливости последнего равенства, воспользовавшись формулой подсчета числа сочетаний без повторений.

II. Составим таблицу значений  при различных значениях n и k. В таблицу 2 занесем значения =1, =1, =1, =1, =2, =1. Заполните остальные строки таблицы, используя свойство сочетаний.

Займемся изучением таблицы 2.

Первые и последние элементы любой строки равны 1, так как ==1. Это равенство будем считать верным и при n=0 (пустое множество своим единственным подмножеством имеет самое себя).

Любой другой элемент таблицы 2 согласно свойству сочетаний, на основании которого составлена таблица, равен сумме двух элементов предшествующей строки: стоящего непосредственно над ним и стоящего над ним слева.

Часто числа  располагают в таблице иначе, так, что каждый элемент таблицы равен сумме двух чисел предшествующей строки, стоящих непосредственно над ним слева и справа. Тогда таблица принимает форму равнобедренного треугольника.

Исследованием свойств такой треугольной таблицы и применениями ее занимался выдающийся ученый Франции Блез Паскаль (1623 —1662). Поэтому рассматриваемую таблицу часто называют треугольником Паскаля. Хотя задолго до Паскаля этот треугольник встречался в работах итальянских и арабских математиков.

Отметим некоторые из свойств треугольника Паскаля.

1.   Сумма чисел k-той строки равна 2^k: ранее было доказано, что +++…+=2^k.

Таблица 2

	0	1	2	3	4	5	6	7	8	9	10	…
0	1											…
1	1	1										…
2	1	2	1									…
3	1	3	3	1								…
4	1	4	6	4	1							…
5	1	5	10	10	5	1						…
6	1	6	15	20	15	6	1					…
7	1	7	21	35	35	21	7	1				…
8	1	8	28	56	70	56	28	8	1			…
9	1	9	36	84	126	126	84	36	9	1		…
10	1	10	45	120	210	252	210	120	45	10	1	…
…	…	…	…	…	…	…	…	…	…	…	…	…

2. Числа каждой строки треугольника, равноудаленные от ее концов, равны между собой. Обоснованием этого свойства служит равенство =.

2. Члены любой строки треугольника Паскаля до середины строки возрастают, а затем убывают.

Задания:

1.    Сколько различных подмножеств имеет множество всех цифр?

2.    Сколько различных делителей, включая 1, имеет число а)2∙3∙5∙7∙11? б) 195?

3.    Сколько различных произведений, кратных 10, можно составить из множителей 2, 7, 11, 9, 3, 5?

4.       С помощью свойства сочетаний =+ докажите равенство: +++…+=.

5.       Пользуясь треугольником Паскаля, найдите числа , .

6.       Напишите 11 строку треугольника Паскаля.

Занятие №10. Бином Ньютона.

Это занятие можно построить на подготовленных учениками ранее в качестве домашнего задания докладах по данной теме.

В процессе самостоятельной подготовки докладов учащиеся овладевают навыками работы с научно-популярной и справочной литературой.

Занятие №11. Решение задач.

Блок задач должен содержать задачи на простое однократное применение какой-либо формулы, задачи, решаемые бесформульными методами, комбинированные задачи.

1.   Имеется 5 видов конвертов без марок и 4 вида марок. Сколькими способами можно выбрать конверт с маркой для посылки и письма?

2.   Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»?

3.   Сколькими способами можно выбрать на шахматной доске белый и черный квадраты, не лежащие на одной горизонтали или одной вертикали?

4.   Сколько можно составить пятибуквенных слов из 7 гласных и 25 согласных букв, если гласные и согласные должны чередоваться?

5.   Сколько существует пятизначных четных чисел, в которых ни одна цифра не повторяется дважды?

6.   Сколько четырехбуквенных слов можно составить из букв слова «кибитка»?

7.   Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие два лица одного пола не сидели рядом?

8.   Сколькими способами можно выбрать 3 краски из имеющихся 5 различных красок?

9.   На школьном вечере присутствуют 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары для танца?

10.Во скольких девятизначных числах все цифры различны?

11.Сколько четырехзначных чисел можно составить из цифр числа 123153?

12.Сколько существует семизначных телефонных номеров, в первых трех цифрах которых не встречаются 0 и 9?

13.Сколькими способами можно выбрать из натуральных чисел от 1 до 30 три натуральных числа так, чтобы их сумма была четной?

14.На прямой взято p – точек, а на параллельной ей прямой еще g – точек. Сколько существует треугольников, вершинами которых являются эти точки?

15.В комнате n лампочек. Сколько всего разных способов освещения комнаты, при которых горит ровно k лампочек?

16.Сколько имеется четырехзначных чисел, у которых каждая следующая цифра меньше предыдущей?

17.Сколькими способами можно рассадить n гостей за круглым столом?

18.Имеется 10 различных книг и 15 различных журналов. Сколькими способами можно составить посылку из 3 книг и 5 журналов?

19.Сколько трехзначных чисел, оканчивающихся цифрой 3?

20.Сколько ожерелий можно составить из 7 различных бусин?

21.Сколькими способами можно разбить множество из 20 элементов на два подмножества так, чтобы одно содержало 3 элемента, а другое – 17?

22.Сколькими способами можно разложить на шахматной доске две ладьи так, чтобы они не били друг друга?

23.Сколько различных двухзначных чисел можно составить из цифр 1, 3, 5, если цифры в числе могут повторяться?

24.Сколько различных предсказаний о распределении 3 трудовых мест можно сделать, если в соревновании принимают участие 10 человек?

25.Сколькими способами можно выбрать 4 числа из 10?

26.В турнире по шахматам каждый участник сыграл с каждым по одной партии, всего было сыграно 36 партий. Определите число участников турнира.

27.В классе имеется 6 сильных математиков. Сколькими способами из них можно составить команду на районную олимпиаду по математике, если от класса можно послать команду от 2 до 4 человек?

28.Сколько различных направлений задают на плоскости вершины треугольника?

29.Из колоды в 36 карт наугад выбирают 2 карты. Сколько возможно случаев, в которых обе карты окажутся тузами?

Занятие №12. Комбинаторика вокруг нас.

К данному итоговому занятию каждый из учащихся должен подготовить проект на тему «Приложения комбинаторики» (в химии, астрономии, геометрии, физике, биологии, теории вероятности, логике, программировании). Это могут быть доклады, сообщения, сопровождающиеся наглядностью, презентации и прочие. Учащиеся могут пользоваться любыми ресурсами, в том числе электронными. Можно им порекомендовать книгу.

Раздел 2. Элементы теории вероятности.

Этот раздел элективного курса представляет собой чрезвычайно яркую, интересную и своеобразную область математики.

Изучение материала сопровождается рассмотрением разнообразных игровых и жизненно интересных примеров с непредсказуемым однозначным результатом. Рассмотрение случайных событий, некоторые трудности психологического характера, вызываемые необычностью объектов изучения, делают курс непростым для усвоения.

Занятие №1. Предмет теории вероятностей. События.

На вводном занятии надо рассказать учащимся о возникновении теории вероятности, об ученых, стоящих у ее истоков. Причем, по мере рассказа учителя, учащиеся могут делать доклады по биографии упомянутых ученых. Темы доклады нужно распределить заранее.

В обыденной жизни, давая какие-либо прогнозы, мы нередко употребляем выражения «вероятность», «вероятно». Например, мы говорим: «Вероятно, сегодня вечером будет дождь». Причём мы отдаём себе отчёт, в каких событиях «мало» вероятности, в каких – «много».

Французский естествоиспытатель Ж.Л.Л. Бюффон в XVIII столетии подбрасывал монету 4040 раз – герб выпал 2048 раз. Математик К. Пирсон в нале прошлого века подбрасывал её 24000 раз – герб выпал 12012 раз. В 70-х г.г. XX века американские естествоиспытатели повторили опыт. При 10000 подбрасываниях герб выпал 4979 раз. Значит, результаты бросаний монеты, хотя каждое из них и является случайным событием, при неоднократном повторении подвластны объективному закону.

Теория вероятностей и изучает закономерности, управляющие массовыми случайными событиями.

С случайными событиями (или явлениями), то есть с такими, которые могут либо произойти, либо не произойти в результате какого-то испытания, мы встречаемся в жизни очень часто.

Ученик извлекает билет – это испытание. Появление при этом билета №13 – случайное событие, билета №5 – другое случайное событие. Выбор наугад какой-то страницы в книге – это испытание. То, что первой буквой на этой странице окажется «м» – это случайное событие.

Например, рассмотрим следующие события:

№№	Условие	Исход
А1	При нагревании проволоки	её длина увеличится
А2	При бросании игральной кости	выпадут 4 очка
А3	При бросании монеты	выпадет герб
А4	При осмотре почтового ящика	найдены три письма
А5	При низкой температуре	вода превратилась в лёд

События А₁, А₅ произойдут закономерно, А₂, А₃, А₄ – случайные.

Событие, которое в данном испытании неизбежно наступит, называется достоверным, а событие, которое в данном испытании никогда не появится – невозможным.

Какие из следующих событий достоверны:

А	Два попадания при трёх выстрелах	+
В	Выплата рубля семью монетами	+
С	Наугад выбранное случайное число не больше 1000	+
D	Наугад выбранное число, составленное из цифр 1,2,3 без повторений, меньше 400	+
E	Выпадение семи очков при бросании игральной кости	-
F	Получение пятёрки на экзамене	+

Назовите невозможные события:

А	Вода в реке замерзла при температуре +25°С	+
В	Появление слова «мама» при случайном наборе букв м, м, а, а	-
С	Появление сразу трёх лайнеров над аэропортом	+
D	Составление трёхзначного числа, состоящего из цифр 1,2,3 и кратного 5	+
E	Появление 17 очков при бросании трёх игральных костей	-

Упражнения:

Для каждого из этих событий определить, каким оно является: невозможным, достоверным или случайным.

1.         Из 26 учащихся класса двое справляют свой день рождения: 1) 25 января; 2) 31 июня.

2.         Случайным образом открывается художественное произведение и находится второе слово на левой странице. Это слово начинается: 1) с буквы М; 2) с буквы Ъ.

3.         Из списка журнала 9 класса (в котором есть и мальчики, и девочки) случайным образом выбран ученик: 1) это мальчик; 2) выбран ученик, которому 15 лет; 3) выбранному ученику 15 месяцев; 4) этому ученику больше двух лет.

4.         Сегодня в Кирове барометр показывает нормальное атмосферное давление. При этом: 1) вода в кастрюле закипит при температуре 70°С; 2) когда температура упала до -3°С, вода в луже замёрзла.

5.         В нашей школе учатся 758 учеников. Событие А={в школе есть ученики с совпадающими днями рождения} является случайным или достоверным. Выясните, произошло ли это событие в вашем классе?

6.         Среди 150 билетов школьной благотворительной лотереи 30 выигрышных. Сколько билетов надо купить, чтобы событие А={вы ничего не выиграете} было невозможным?

7.         В 10 «Г» классе учится 16 мальчиков и 10 девочек. Какие из следующих событий являются невозможными, какие случайными, какие – достоверными:

А={ в классе есть два человека, родившихся в разные месяцы};

В={в классе есть два человека, родившихся в одном месяце};

С={в классе есть два мальчика, родившихся в одном месяце};

D={в классе есть две девочки, родившиеся в одном месяце};

Е={все мальчики родились в разные месяцы};

F={все девочки родились в разные месяцы};

К={есть мальчик и девочка, родившиеся в одном месяце};

М={ есть мальчик и девочка, родившиеся в разные месяцы}.

8.         Около школы останавливаются автобусы трёх маршрутов, идущих в сторону лесозавода: № 5, № 13 и № 23. Интервал в движении автобусов каждого маршрута колеблется от 8 до 10 минут. Когда Саша, Маша, Кристина и Катя подошли к остановке, от неё отошёл автобус № 13, а ещё через 6 минут подошёл автобус № 5. После этого каждый из ребят высказал своё мнение о том, автобус какого маршрута будет следующим:

Саша: Следующим обязательно будет № 23.

Маша: Возможно, что следующим будет № 23.

Кристина: Возможно, что следующим будет № 13.

Катя: Невозможно, что следующим будет № 5.

С кем из ребят вы согласны, а с кем нет? Объясните сделанный выбор.

9. На дорогу от дома до школы Миша тратит от 10 до 15 минут, если идёт пешком, и от 2 до 3 минут, если едет на автобусе. При каких интервалах движения автобусов событие А=={по пути в школу Мишу обгонит хотя бы один автобус} будет невозможным, при каких – случайным, при каких – достоверным?

После знакомства с понятием «случайное событие» учащиеся должны уметь приводить примеры таких событий из жизни и отличать их от неслучайных.

Занятие №2. Виды случайных событий.

События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. В противном случае события называются совместными.

Например, события «пошел дождь» и «наступило утро» являются совместными, а события «наступило утро» и «наступила ночь» - несовместными.

Задачи:

1.         В сыгранной Катей и Ларисой партии в шахматы определить совместные и несовместные события, если: 1) Катя выиграла, Лариса проиграла; 2) Катя проиграла, Лариса проиграла.

2. Из событий: 1) «идёт дождь»; 2) «на небе нет ни облака»; 3) «наступило лето» - составить всевозможные пары и выявить среди них пары совместных и пары несовместных событий.

3. Из событий: 1) «наступило утро»; 2) «сегодня по расписанию 6 уроков»; 3) «сегодня 1 января»; 4) «температура воздуха в Мариинске +30°С» - составить всевозможные пары и выявить среди них пары совместных и пары несовместных событий.

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Например, «выпадение герба» и «выпадение цифры» при бросании монеты – равновозможные события. «Изъятие из набора домино дубля» и «изъятие из набора домино костяшки с разными очками» - неравновозможные события, так как дублей в наборе домино всего 7, а остальных костяшек 21.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.

Например, попадание и промах при выстреле; появление 1, 2, 3, 4, 5, 6 очков при бросании игральной кости.

Если два единственно возможных события образуют полную группу, то их называют противоположными (выигрыш и не выигрыш, попадание и промах). Если одно из двух противоположных событий обозначено через А, то другое принято обозначать .

Задачи: