Навигация
Теоремы Ролля, Коши, Лагранжа. Правило Лопиталя
6687
знаков
0
таблиц
3
изображения
Реферат
на тему:
"Теоремы Ролля, Коши, Лагранжа. Правило Лопиталя"
1. Теорема Ролля
Знание производной некоторой функции позволяет судить о характерных особенностях в поведении этой функции. В основе всех таких исследований лежат некоторые простые теоремы, называемые теоремами о среднем в дифференциальном исчислении.
Начнем рассмотрение таких теорем с теоремы, связываемой с именем французского математика Ролля (1652–1719).
Теорема 1.1. Если функция 
непрерывна на отрезке 
, дифференцируема во всех его внутренних точках, а на концах отрезка 
, 
обращается в ноль, то существует, по крайней мере, одна точка 
, в которой 
.
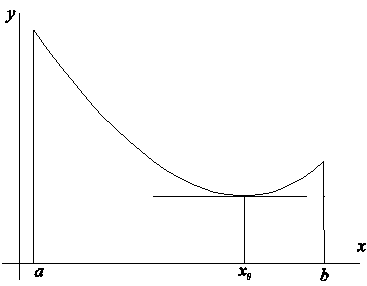
Доказательство. Так как функция непрерывна на отрезке , то, согласно свойству 11.1.1, она должна достигать хотя бы один раз на этом отрезке своего минимума 
и максимума 
(рис. 1.1).
Если 
, функция постоянна, то есть 
. Но в этом случае 
для любого 
.
В общем случае 
, и хотя бы одно из этих чисел не равно нулю. Предположим для определенности, что 
. Тогда существует точка 
, в которой 
.
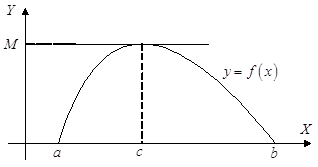
Рис. 1.1
Так как рассматриваемое значение является максимальным, то для него справедливо, что 
для 
и 
.
Рассмотрим пределы
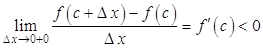для
и
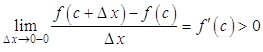для .
Так как оба предела равны производной функции в одной и той же точке , то они равны между собой. Значит, из одновременности 
и 
следует, что , что и требовалось доказать.
Следует отметить, что данная теорема справедлива и в том случае, когда на концах отрезка функция не обращается в ноль, но принимает равные значения 
. Доказательство проводится аналогично.
Геометрический смысл данной теоремы следующий: если непрерывная кривая пересекает ось 
в двух точках , или принимает в них равные значения, то, по крайней мере, в одной точке между 
и 
касательная к кривой параллельна оси .
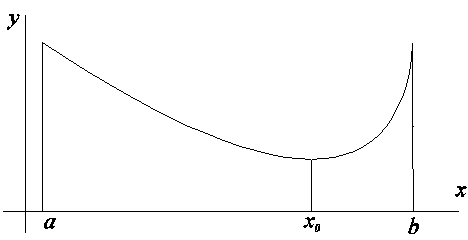
Необходимо отметить, что если не во всех точках у рассматриваемой функции существует производная, то теорема может не выполняться. Это касается, например, функции 
(рис. 1.2):
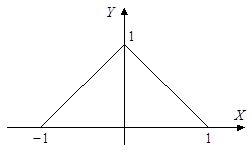
Рис. 1.2
Данная функция непрерывна на отрезке 
и обращается в ноль на его концах, но ни в одной точке внутри отрезка производная не равна нулю.
Похожие работы
... типов неопределенностей. Примеры для этого и последующего раздела были взяты из [Марон]. В четвертом разделе приведен вывод формулы Тейлора и показано применение формулы Тейлора для нахождения эквивалентных функций и вычисления пределов. 1. Бесконечно малые и их сравнения; символы "o малое" и "о большое" Определение. Бесконечно малой в x0 называется функция f (x) такая, что Свойства ...
рема Ферма: Если функция у=f(х) имеет в точке х0 локальный экстремум и дифференцируема в этой точке, то ее производная f'(х0) равна нулю. Док-во: Проведем его для случая максимума в точке х0. Пусть (х0-d, х0+d) - та окрестность, для точек которой выполняется неравенство Здесь возможно как 1 и 2 варианты, но | ∆х| <δ При ∆х>0, будет ∆y:∆x ...
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... вытекает, что f'(c)=0. #30 Теорема (Ролля). Если функция y=f(x) непрерывна на [а, b], дифференцируема на (а, b) и f (а) ==f(b), то существует точка c0(а,b), такая, что f'(c)=0. Доказательство. Если f постоянна на [а, b], то для всех c(a, b) производная f'(c)=0. Будем теперь считать, что f непостоянна на [а, b]. Так как f непрерывна на [а, b], то существует точка x1 [а, ...
0 комментариев